算法拾遗二十七之暴力递归到动态规划七
- 题目一【数组累加和最小的】
- 题目二
- 什么暴力递归可以继续优化
- 暴力递归和动态规划的关系
- 面试题和动态规划的关系
- 如何找到某个问题的动态规划方式
- 面试中设计暴力递归的原则
- 知道了暴力递归的原则 然后设计
- 常见的四种尝试模型
- 如何分析有没有重复解
- 暴力递归到动态规划的套路
- 动态规划的进一步优化
- N皇后问题
题目一【数组累加和最小的】

找较小的集合最接近两个集合总和的一半:
public static int right(int[] arr) {
if (arr == null || arr.length < 2) {
return 0;
}
//统计所有数的累加和
int sum = 0;
for (int num : arr) {
sum += num;
}
return process(arr, 0, sum / 2);
}
// arr[i...]从i位置出发及其后面的数可以自由选择,
// 请返回累加和尽量接近rest,但不能超过rest的情况下,最接近的累加和是多少?
public static int process(int[] arr, int i, int rest) {
if (i == arr.length) {
return 0;
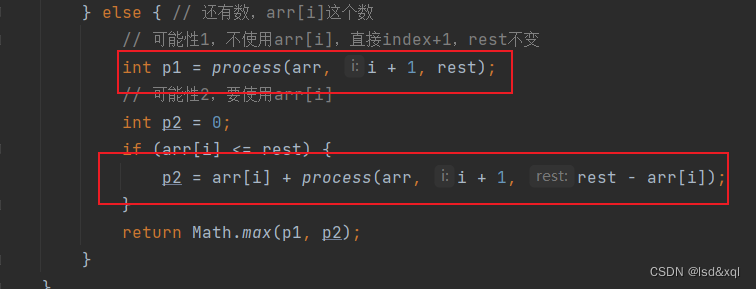
} else { // 还有数,arr[i]这个数
// 可能性1,不使用arr[i],直接index+1,rest不变
int p1 = process(arr, i + 1, rest);
// 可能性2,要使用arr[i]
int p2 = 0;
if (arr[i] <= rest) {
p2 = arr[i] + process(arr, i + 1, rest - arr[i]);
}
return Math.max(p1, p2);
}
}
改dp,有两个可变参数:
i变化范围为0-N,rest变化范围,从0-sum/2,不会超过此范围。
先看basecase:
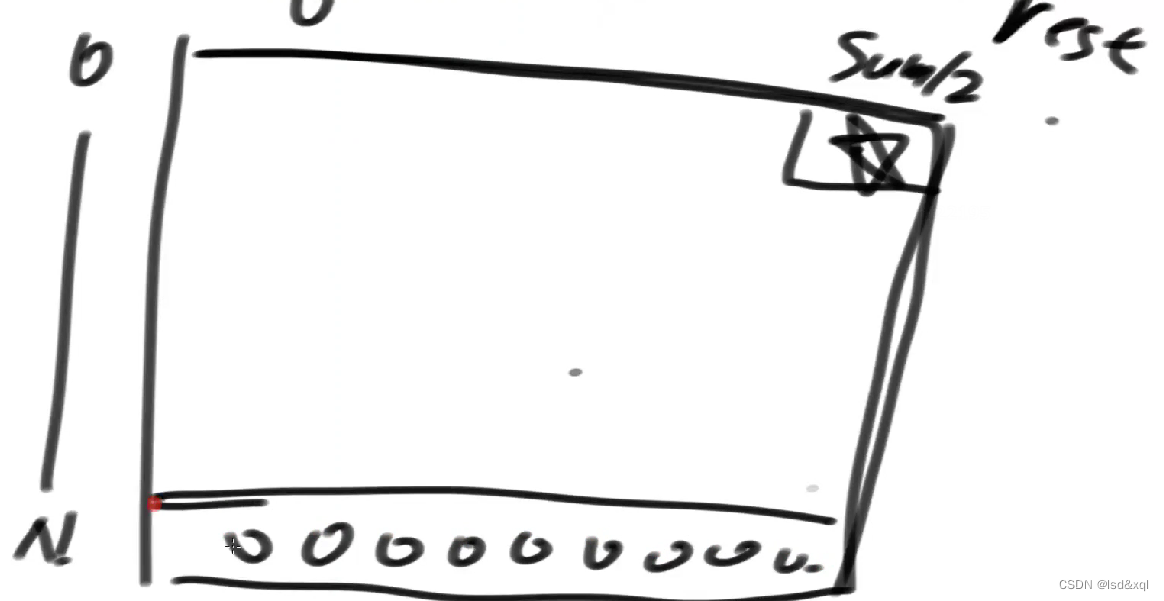
分析普遍位置依赖关系:
i位置依赖于i+1位置
public static int dp1(int[] arr) {
if (arr == null || arr.length < 2) {
return 0;
}
int sum = 0;
for (int num : arr) {
sum += num;
}
sum /= 2;
int N = arr.length;
int[][] dp = new int[N + 1][sum + 1];
/*
int p1 = process(arr, i + 1, rest);
// 可能性2,要使用arr[i]
int p2 = 0;
if (arr[i] <= rest) {
p2 = arr[i] + process(arr, i + 1, rest - arr[i]);
}
*/
for (int i = N - 1; i >= 0; i--) {
for (int rest = 0; rest <= sum; rest++) {
int p1 = dp[i + 1][rest];
int p2 = 0;
if (arr[i] <= rest) {
p2 = arr[i] + dp[i + 1][rest - arr[i]];
}
dp[i][rest] = Math.max(p1, p2);
}
}
return dp[0][sum];
}
public static int[] randomArray(int len, int value) {
int[] arr = new int[len];
for (int i = 0; i < arr.length; i++) {
arr[i] = (int) (Math.random() * value);
}
return arr;
}
public static void printArray(int[] arr) {
for (int num : arr) {
System.out.print(num + " ");
}
System.out.println();
}
public static void main(String[] args) {
int maxLen = 20;
int maxValue = 50;
int testTime = 10000;
System.out.println("测试开始");
for (int i = 0; i < testTime; i++) {
int len = (int) (Math.random() * maxLen);
int[] arr = randomArray(len, maxValue);
int ans1 = right(arr);
int ans2 = dp1(arr);
if (ans1 != ans2) {
printArray(arr);
System.out.println(ans1);
System.out.println(ans2);
System.out.println("Oops!");
break;
}
}
System.out.println("测试结束");
}
题目二

public static int right1(int[] arr) {
if (arr == null || arr.length < 2) {
return 0;
}
int sum = 0;
for (int num : arr) {
sum += num;
}
if ((arr.length & 1) == 0) {
return process1(arr, 0, arr.length / 2, sum / 2);
} else {
return Math.max(process1(arr, 0, arr.length / 2, sum / 2), process1(arr, 0, arr.length / 2 + 1, sum / 2));
}
}
public static int process1(int[] arr, int i, int picks, int rest) {
if (i == arr.length) {
//没有数的情况,没法调返回一个-1表示这个过程不能使用
return picks == 0 ? 0 : -1;
} else {
//还有数挑
//第一种选择不挑当前数
int p1 = process1(arr, i + 1, picks, rest);
int p2 = -1;
int next = -1;
if (arr[i] <= rest) {
next = process1(arr, i + 1, picks - 1, rest - arr[i]);
}
if (next != -1) {
//如果后续是有效的才有可能性2
p2 = arr[i] + next;
}
return Math.max(p1,p2);
}
}
改dp:三个可变参数可用一个三维dp解决
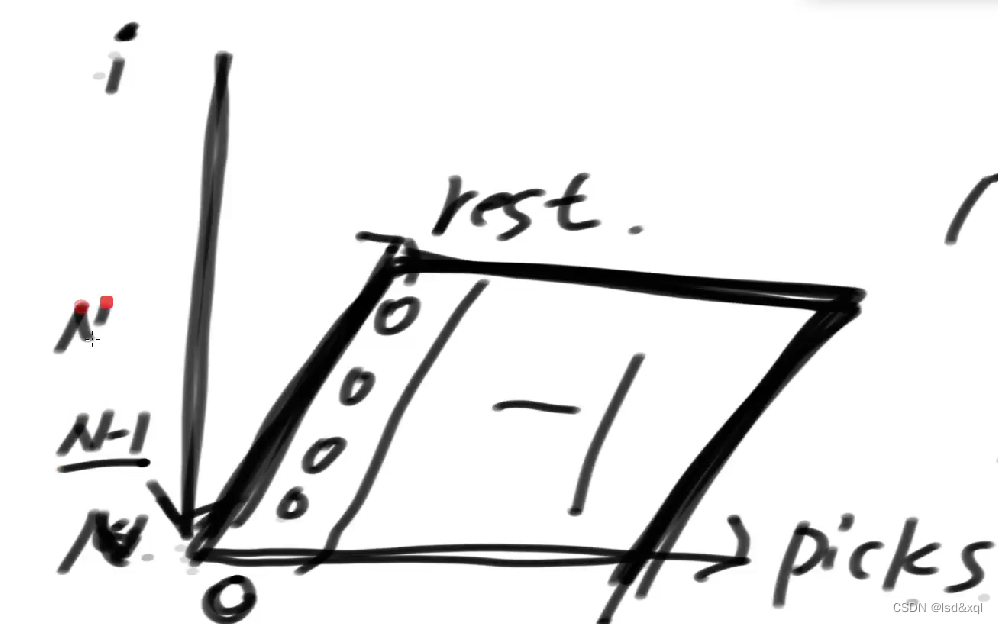
public static int dp4(int[] arr) {
if (arr == null || arr.length < 2) {
return 0;
}
int sum = 0;
for (int num : arr) {
sum += num;
}
sum /= 2;
int N = arr.length;
int M = (N + 1) / 2;
int[][][] dp = new int[N + 1][M + 1][sum + 1];
for (int i = 0; i <= N; i++) {
for (int j = 0; j <= M; j++) {
for (int k = 0; k <= sum; k++) {
dp[i][j][k] = -1;
}
}
}
/* if (i == arr.length) {
//没有数的情况,没法调返回一个-1表示这个过程不能使用
return picks == 0 ? 0 : -1;
}*/
for (int rest = 0; rest <= sum; rest++) {
dp[N][0][rest] = 0;
}
for (int i = N - 1; i >= 0; i--) {
for (int picks = 0; picks <= M; picks++) {
for (int rest = 0; rest <= sum; rest++) {
/* //还有数挑
//第一种选择不挑当前数
int p1 = process1(arr, i + 1, picks, rest);
int p2 = -1;
int next = -1;
if (arr[i] <= rest) {
next = process1(arr, i + 1, picks - 1, rest - arr[i]);
}
if (next != -1) {
//如果后续是有效的才有可能性2
p2 = arr[i] + next;
}
return Math.max(p1, p2);*/
int p1 = dp[i + 1][picks][rest];
int p2 = -1;
int next = -1;
if (picks - 1 >= 0 && arr[i] <= rest) {
next = dp[i + 1][picks - 1][rest - arr[i]];
}
if (next != -1) {
p2 = arr[i] + next;
}
dp[i][picks][rest] = Math.max(p1,p2);
}
}
}
if ((arr.length & 1) == 0) {
return dp[0][arr.length / 2][sum];
} else {
return Math.max(dp[0][arr.length / 2][sum], dp[0][(arr.length / 2) + 1][sum]);
}
}
什么暴力递归可以继续优化


暴力递归和动态规划的关系

面试题和动态规划的关系

如何找到某个问题的动态规划方式

面试中设计暴力递归的原则

知道了暴力递归的原则 然后设计

常见的四种尝试模型

如何分析有没有重复解

暴力递归到动态规划的套路

动态规划的进一步优化

N皇后问题

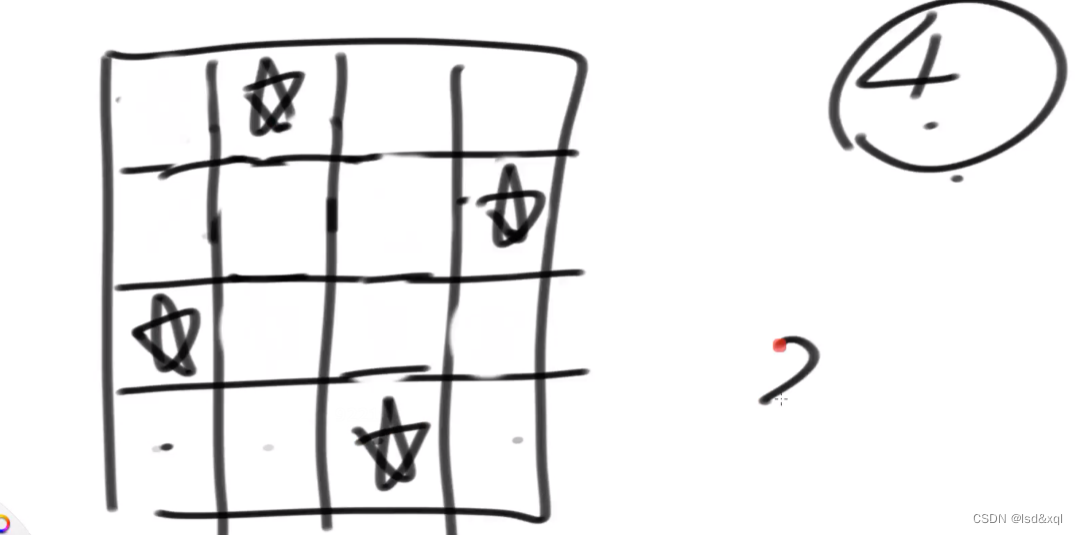
如上算是一种解,考虑皇后的时候一行一行的填入皇后,每一行填入一个皇后,这样就不用检查两个皇后是否共行了。
之前的某个皇后在(x,y),然后当前位置在(甲,乙)位置
如果y==乙或者甲减去x的绝对值等于y-乙的绝对值【共斜线】
复杂度为O(n的n次方)
每一行都有n种决策
public static int num1(int n) {
if (n < 1) {
return 0;
}
int[] record = new int[n];
return process1(0, record, n);
}
// 当前来到i行,一共是0~N-1行
// 在i行上放皇后,所有列都尝试
// 必须要保证跟之前所有的皇后不打架
// int[] record record[x] = y 之前的第x行的皇后,放在了y列上,一维数组的列号表示n皇后的行号
// 返回:不关心i以上发生了什么,i.... 后续有多少合法的方法数
public static int process1(int i, int[] record, int n) {
//i来到n位置未发生打架
if (i == n) {
return 1;
}
int res = 0;
// i行的皇后,放哪一列呢?j列,
for (int j = 0; j < n; j++) {
if (isValid(record, i, j)) {
record[i] = j;
res += process1(i + 1, record, n);
}
}
return res;
}
/**
* 判断是否发生打架
*
* @param record
* @param i
* @param j
* @return
*/
public static boolean isValid(int[] record, int i, int j) {
// 0..i-1,检查0->i-1行的皇后是否发生打架
for (int k = 0; k < i; k++) {
if (j == record[k] || Math.abs(record[k] - j) == Math.abs(i - k)) {
return false;
}
}
return true;
}
位运算优化常数时间:
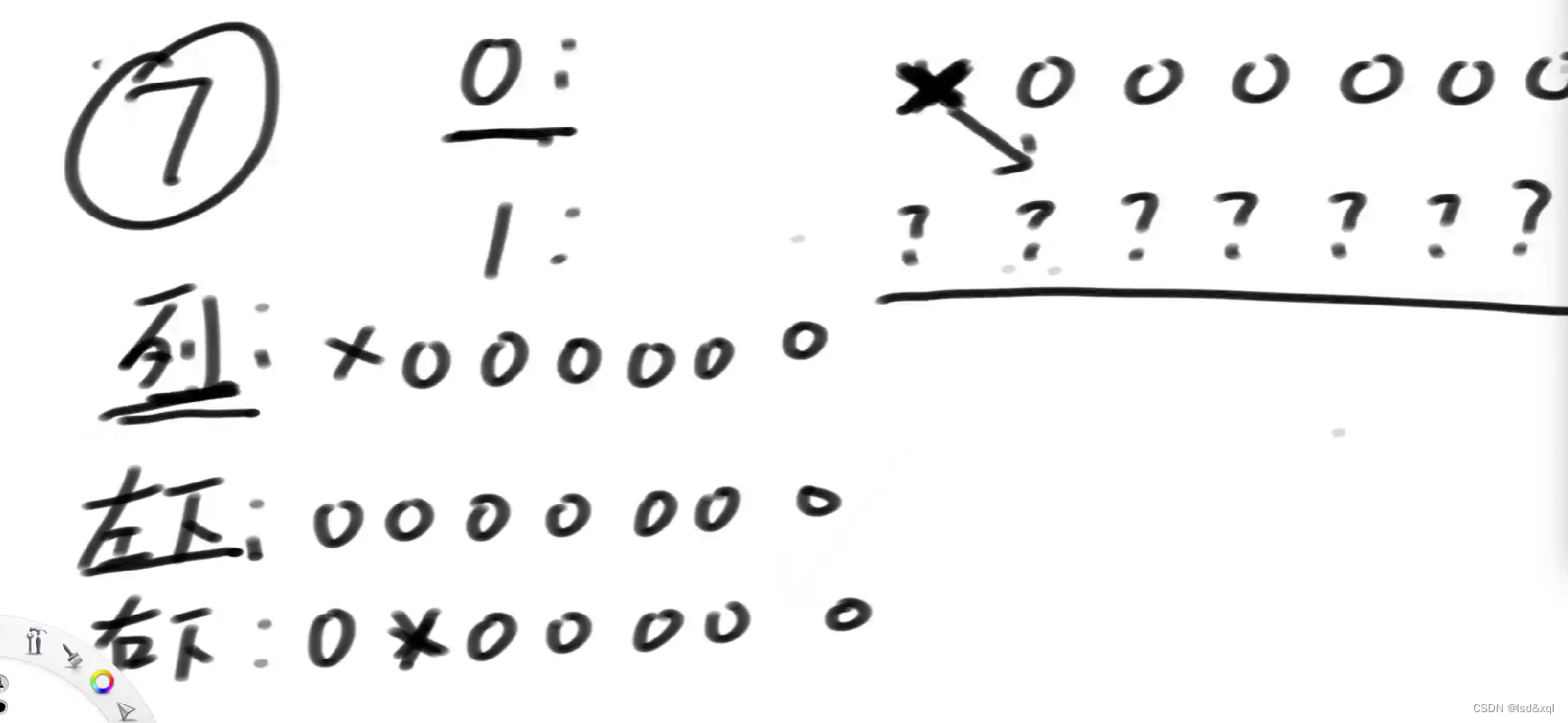
能选的位置是列或上左下与右下还是0的位置。
同理再定义一个第0行的x位置是皇后放置的位置,或出来三个方框的位置是第一行不能选的。
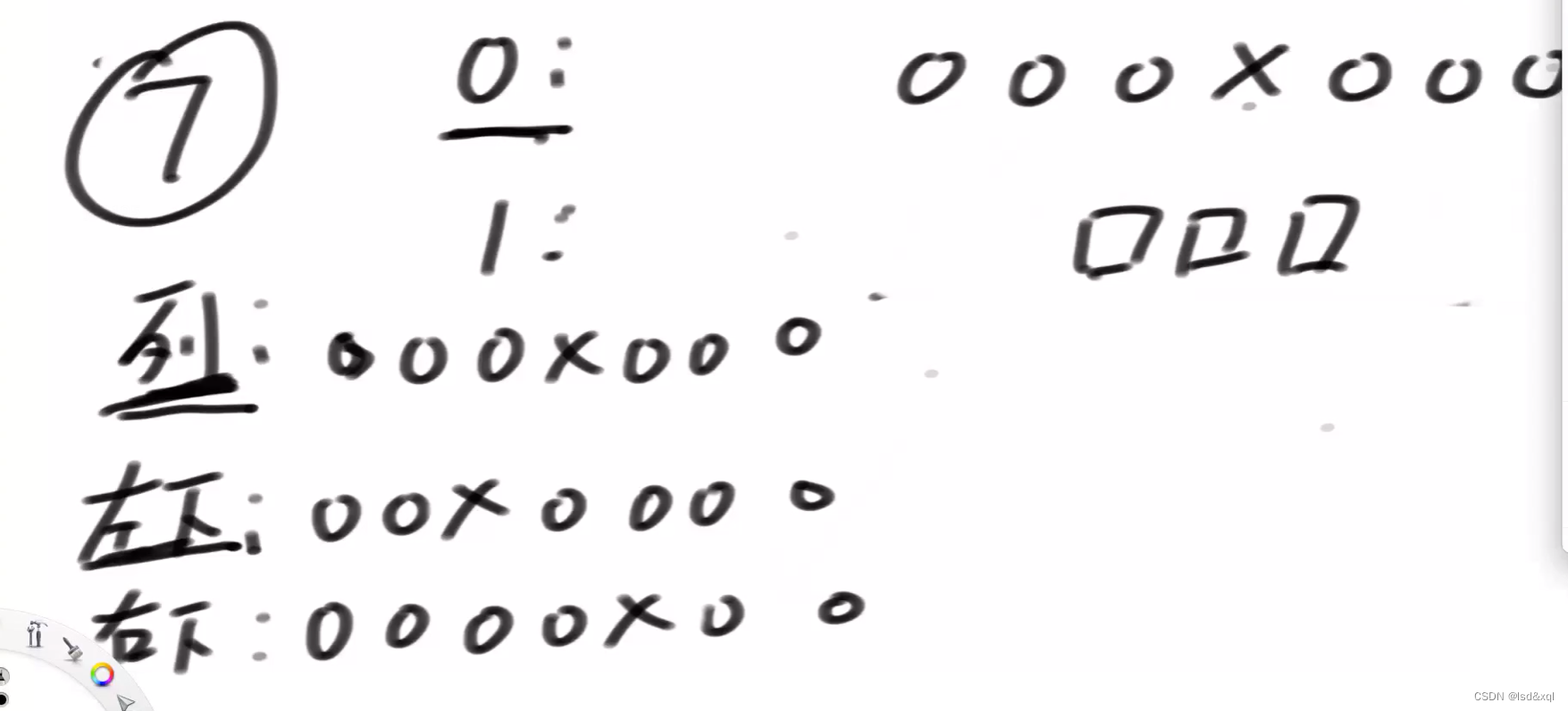
每次放一个皇后都要更新列限制,左下限制以及右下限制。
假设某个时刻是这样的:
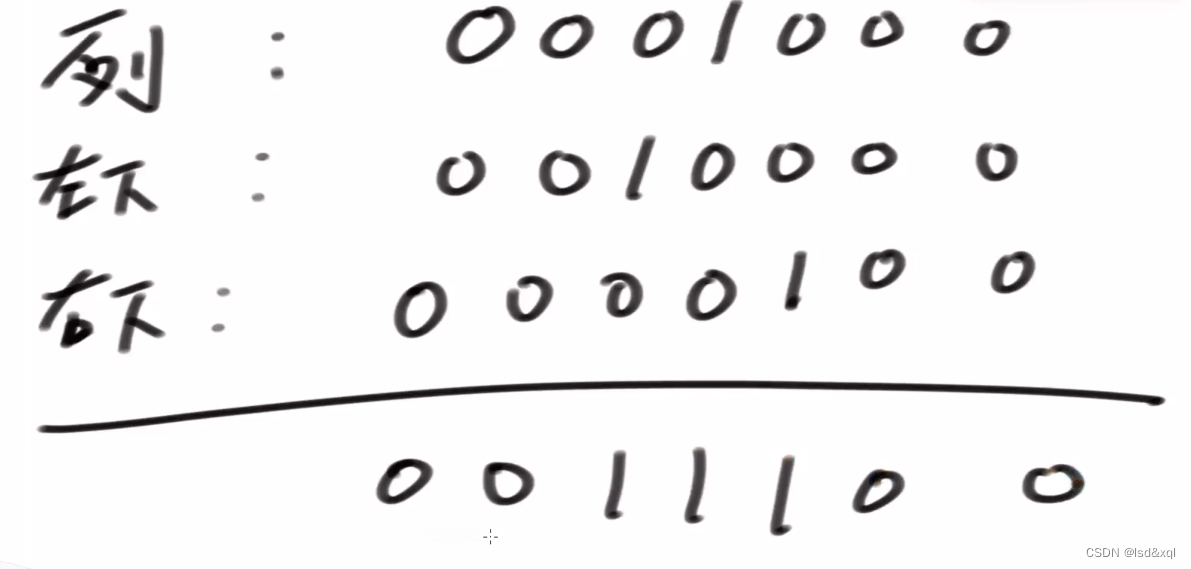
最后是1的不能放皇后是0的可以,然后整体取反变成其他的全1中间的三个1变成三个0
limit是0…011111110…0,然后与一下得到limit=1100011,其中1是能放n皇后的位置
// 请不要超过32皇后问题
public static int num2(int n) {
if (n < 1 || n > 32) {
return 0;
}
// 如果你是13皇后问题,limit 最右13个1,其他都是0,通过整数的位来标记皇后
int limit = n == 32 ? -1 : (1 << n) - 1;
return process2(limit, 0, 0, 0);
}
// 7皇后问题
// limit : 0....0 1 1 1 1 1 1 1
// 之前皇后的列影响:colLim
// 之前皇后的左下对角线影响:leftDiaLim
// 之前皇后的右下对角线影响:rightDiaLim
public static int process2(int limit, int colLim, int leftDiaLim, int rightDiaLim) {
//列影响等于了limit
if (colLim == limit) {
return 1;
}
// pos中所有是1的位置,是你可以去尝试皇后的位置
int pos = limit & (~(colLim | leftDiaLim | rightDiaLim));
int mostRightOne = 0;
int res = 0;
while (pos != 0) {
mostRightOne = pos & (~pos + 1);
pos = pos - mostRightOne;
res += process2(limit, colLim | mostRightOne, (leftDiaLim | mostRightOne) << 1,
(rightDiaLim | mostRightOne) >>> 1);//无符号右移
}
return res;
}