人菜瘾大还是忍不住打了这场比赛，b卡了半小时，甚至还写了一个最长公共子序列然后喜提wa2，但是c,d还是过的比较快，最后排名rk175有惊无险的上分了，e题赛时一眼想出思路，但是我的实现能力有限，没能在赛时通过，赛后补了这道题，狠狠抽打了我自己的码力，马上要ec了，未来的队友还需要我去当代码手实现思路，在这里狠狠拷打一下我自己。

简要题意 给你一颗树，问你划分成若干条颜色段，颜色段必须联通，并且颜色段每个点的深度不同，问你颜色段最小值的最大值是多少。

看到这个题，第一反应就是做贪心，我们可以比较套路性地想到我们可以从底往上做，我们先处理子树，再处理当前节点。根据题意，我们不难发现，这个颜色段一定是一条链，而且是从上到下平铺在树上，即链上的任意两点的lca为$lca(u,v)==u或lca(u,v)==u$。

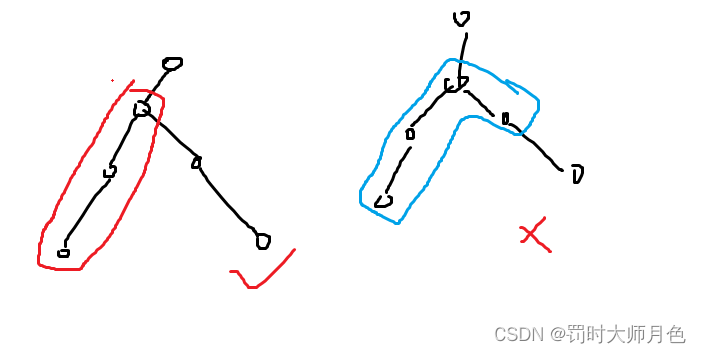
然后我们考虑由下到上贪心，我们对于一个点$u$，我们维护两个值，一个是节点u所在的颜色段的长度，当前子树颜色段的最小值。

接下来考虑转移我们对于一个节点$u$,我们可以从儿子所在的链种选择一条链，然后接上节点u。

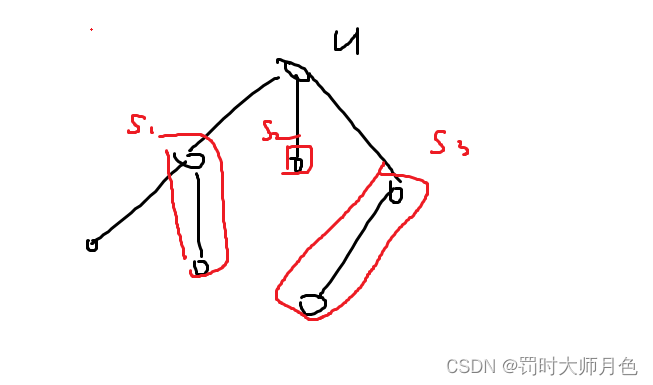
如上图所示，我们对于一个节点u，我们可以从三个儿子维护的链中选择一个接上u,如果我们采取接上s1,则为下图所示。

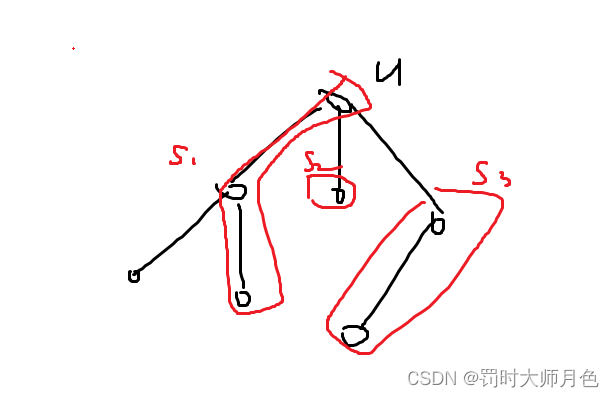
然后我们现在有若干个儿子，我们该如何去接儿子呢，我们先对儿子的链大小进行排序，我们应该去接长度最短的链。原因：考虑贪心地让最小值最大，如果我们考虑不接长度最短的，答案一定小于等于长度最短的链，若接到长度最短的链，答案就小于等于次小值，答案更大，更优，所以我们一定接在最短的一条链上， 然后没有被接到$u$的链，我们把他放到u子树颜色段的最小值去维护(即第二关键字),然后我们确定一个根，然后$dfs$一遍我们就可以得到某个点为根时的答案了，我们如何求全局最小值，我们考虑暴力地把每个根都跑一遍，时间复杂度是$O(n^2)$，我们就考虑换根dp的思路去做，用换根dp的思路去维护这种转移即可。
代码实现难度比较大，我写了一个最小次小的封装类，然后维护不同的信息即可。

双倍经验！
代码的大致思路类似于1778E，可以参考我之前写的博文。

代码

#include <iostream>
#include <cmath>
#include <algorithm>
#include <cstring>
#include <bits/stdc++.h>

#define x first
#define y second 

#define int long long 

using namespace std ;

int read(){
	int res = 0 , flag = 1 ;
	char c = getchar() ;
	while(!isdigit(c)){
		if(c == '-') flag = -1 ;
		c = getchar() ;
	}
	while(isdigit(c)){
		res = (res << 1) + (res << 3) + (c ^ 48) ;
		c = getchar() ;
	}
	return res * flag ; 
}

void write(int x){
	if(x < 0) {
		putchar('-') ;
		x = - x ;
	}
	if(x >= 10) write(x / 10) ;
	putchar('0' + x % 10) ;
}

void write(int x , char c){
	write(x) ;
	putchar(c) ; 
}

const int N = 2e5 + 10 ;
typedef pair<int , int> pii ;
typedef pair<double ,double> pdd ;
const int mod = 998244353 ;
const int inf = 1e9 + 10 ;
const int M = 2 * N ;

struct T{
	int a[2] = {inf , inf} ;
	void insert(int x){
		if(a[0] >= x) a[1] = a[0] , a[0] = x ;
		else a[1] = min(a[1] , x) ;   		
	}
	void r(){
		if(a[0] > a[1]) swap(a[0] , a[1]) ; 
	}
	T operator+(T& b)const{
		T c ;
		c.a[0] = a[0] ;
		c.a[1] = a[1] ;	
		c.insert(b.a[0]) ;
		c.insert(b.a[1]) ;
		return c;
	}
	T(){
		
	}
	T(int x , int y){
		a[0] = x ,  a[1] = y ;
	}
} ;

int h[N] , e[M] , ne[M] , idx ;

void add(int a , int b){
	e[idx] = b , ne[idx] = h[a] , h[a] = idx ++ ; 
}

pii dp[N] , f[N] ;

void dfs(int u , int v){
	T t ;  
	int res = inf ; 
	for(int i = h[u] ; ~i ; i = ne[i]){
		int j = e[i] ;
		if(j == v) continue ;
		dfs(j , u) ;
		t.insert(dp[j].x) ; 
		res = min(res , dp[j].y) ;
	}
	if(t.a[0] == inf) dp[u].x = 1 ;
	else dp[u].x = t.a[0] + 1 ;
	dp[u].y = min(t.a[1] , res) ; 
}

int ans ;

void dfs1(int u , int v){
	T t ;
	// cout << u << " " << v << " " << f[v].x << " " << f[v].y << endl ;
	int res = inf ;
	for(int i = h[u] ; ~i ; i = ne[i]){
		int j = e[i] ;
		if(j == v) continue ;
		t.insert(dp[j].x) ;
		res = min(res , dp[j].y) ;
	}
	t.insert(f[v].x) ;
	res = min(res , f[v].y) ;
	// cout << "res" << res << endl ;
	ans = max(ans , min(t.a[0] + 1 , min(res , t.a[1]))) ;
	
	vector<T> pre(1) , suf(1) ;
	vector<int> p(1 , inf) , s(1 , inf) ; 
	int cnt = 0 ;
	for(int i = h[u] ; ~i ; i = ne[i]){
		int j = e[i] ;
		if(j == v) continue ;
		++ cnt ; 
		p.push_back(dp[j].y) ;
		s.push_back(dp[j].y) ;
		pre.push_back(T(dp[j].x , inf)) ;
		suf.push_back(T(dp[j].x , inf)) ; 
	}
	pre.push_back(T(inf , inf)) ;
	suf.push_back(T(inf , inf)) ;
	p.push_back(inf) ;
	s.push_back(inf) ;
	for(int i = 1 ; i <= cnt ; i ++){
		pre[i] = pre[i] + pre[i - 1] ;
		p[i] = min(p[i] , p[i - 1]) ;
	}
	for(int i = cnt ; i ; i --){
		suf[i] = suf[i + 1] + suf[i] ;
		s[i] = min(s[i] , s[i + 1]) ; 
	}
	cnt = 0 ; 
	for(int i = h[u] ; ~i ; i = ne[i]){
		int j = e[i] ;
		if(j == v) continue ; 
		++ cnt ;
		T tt ;
		int rr = inf ;
		rr = min(rr , f[v].y) ;
		rr = min(p[cnt - 1] , rr) ;
		rr = min(s[cnt + 1] , rr) ;
		tt.insert(f[v].x) ;
		tt = tt + pre[cnt - 1] ;
		tt = tt + suf[cnt + 1] ;
		rr = min(tt.a[1] , rr) ;
		if(tt.a[0] == inf) f[u] = {1 , rr} ;
		else
			f[u] = {tt.a[0] + 1 , rr} ; 
		dfs1(j , u) ; 
	}
	
}
void solve() {
	int n = read() ;
	for(int i = 1 ; i <= n ; i ++) h[i] = -1 ; 
	idx = 0 ;
	for(int i = 1 ; i < n ; i ++){
		int a = read() , b = read() ;
		add(a , b) , add(b , a) ; 
	}
	dfs(1 , 1) ; 
	f[0] = {inf , inf} ;
	ans = 0 ; 
	dfs1(1 , 0) ; 
	// cout << min(dp[1].x , dp[1].y) << endl ;
	write(ans , '\n') ;
}

signed main(void){
	int T = read() ;
	while(T --)
		solve() ; 
}