数学知识
文章目录
- 数学知识
- 一、质数
- 一、试除法判定质数
- 二、试除法分解质因数
- 三、朴素筛法求素数
- 四、线性筛法求素数
- 二、约数
- 一、试除法求所有约数
- 二、约数个数约数之和
- 三、欧几里得算法
- 三、欧拉函数
- 一、欧拉函数的定义
- 二、筛法求欧拉函数
- 四、快速幂
- 一、快速幂
- 二、快速幂求逆元
- 扩展欧几里得
- 一、扩展欧几里得算法
- 二、线性同余方程
- 高斯消元
- 一、高斯消元解线性方程组
- 二、高斯消元解异或线性方程组
- 组合数
- 一、求组合数 I
- 二、组合数 II
- 三、求组合数 III
- 四、求组合数 IV
- 五、卡特兰数
- 容斥原理
一、质数
在大于1的整数中,如果只包含1和本身这两个约数,就称为质数,或者叫素数。
一、试除法判定质数
bool is_prime(int x)
{
if (x < 2) return false;
for (int i = 2; i <= x / i; i ++ )
if (x % i == 0)
return false;
return true;
}
二、试除法分解质因数
//x中最多只包含一个大于sqrt(x)的质因子
void divide(int x)
{
for (int i = 2; i <= x / i; i ++ )
if (x % i == 0) //一定是质数
{
int s = 0;
while (x % i == 0) x /= i, s ++ ;
cout << i << ' ' << s << endl;
}
if (x > 1) cout << x << ' ' << 1 << endl;
cout << endl;
}
三、朴素筛法求素数
思想
//埃氏筛法(nloglogn)
int primes[N], cnt; // primes[]存储所有素数
bool st[N]; // st[x]存储x是否被筛掉
void get_primes(int n)
{
for (int i = 2; i <= n; i ++ )
{
if (st[i]) continue;
primes[cnt ++ ] = i;
for (int j = i + i; j <= n; j += i)
st[j] = true;
}
}
四、线性筛法求素数
多用
//n只会被最小质因子筛掉
//1.i%pj==0
// pj一定是i的最小质因子,pj一定是pj*i的最小质因子
//2.i%pj!=0
pj一定小于i的所有质因子,pj也一定是pj*i的最小质因子
//对于一个合数x,假设pj是x的最小质因子,当i枚举到x/pj的时候,就一定会筛掉
int primes[N], cnt; // primes[]存储所有素数
bool st[N]; // st[x]存储x是否被筛掉
void get_primes(int n)
{
for (int i = 2; i <= n; i ++ )
{
if (!st[i]) primes[cnt ++ ] = i;
for (int j = 0; primes[j] <= n / i; j ++ )
{
st[primes[j] * i] = true;
if (i % primes[j] == 0) break; //primes[j]一定是i的最小质因子
}
}
}
二、约数
一、试除法求所有约数
vector<int> get_divisors(int x)
{
vector<int> res;
for (int i = 1; i <= x / i; i ++ )
if (x % i == 0)
{
res.push_back(i);
if (i != x / i) res.push_back(x / i);
}
sort(res.begin(), res.end());
return res;
}
二、约数个数约数之和
//int范围内约数个数最多的数有约数1500左右
如果 N = p1^c1 * p2^c2 * ... *pk^ck //pi为质因数
约数个数: (c1 + 1) * (c2 + 1) * ... * (ck + 1)
约数之和: (p1^0 + p1^1 + ... + p1^c1) * ... * (pk^0 + pk^1 + ... + pk^ck)
三、欧几里得算法
int gcd(int a,int b)
{
return b?gcd(b,a%b):a;
}
int gcd(int a,int b)
{
if(a%b==0) return b;
return gcd(b,a%b);
}
三、欧拉函数
欧拉定理:若a与n互质,则a^ϕ(n)≡1(mod n)
一、欧拉函数的定义
1∼N 中与 N 互质的数的个数被称为欧拉函数,记为 ϕ(N)。
若在算数基本定理中,N=p1a1p2a2…pm^am,则:
ϕ(N) = N×(1-1/p1)×(1−1/p2)×…×(1−1/pm)
输入格式
第一行包含整数 n。
接下来 n 行,每行包含一个正整数 ai。
输出格式
输出共 n 行,每行输出一个正整数 ai 的欧拉函数。
数据范围
1≤n≤100,
1≤ai≤2×10^9
输入样例:
3
3
6
8
输出样例:
2
2
4
//容斥原理
//从1~N中去掉p1,p2...pk的所有倍数
//加上pi*pj的倍数
//减去pi*pj*pk的倍数
//以此类推
#include<iostream>
using namespace std;
int main()
{
int n;
cin>>n;
while(n--)
{
int a;
cin>>a;
int res=a;
for(int i=2;i<=a/i;i++)
{
if(a%i==0)
{
while(a%i==0) a/=i;
res=res/i*(i-1); //res=res*(1-1/i);
}
}
if(a>1) res=res/a*(a-1);
cout<<res<<endl;
}
return 0;
}
二、筛法求欧拉函数
给定一个正整数 n,求 1∼n 中每个数的欧拉函数之和。
输入格式
共一行,包含一个整数 n。
输出格式
共一行,包含一个整数,表示 1∼n中每个数的欧拉函数之和。
数据范围
1≤n≤106
输入样例:
6
输出样例:
12
#include<iostream>
using namespace std;
typedef long long LL;
const int N=1000010;
int prime[N],cnt;
int phi[N];
bool st[N];
LL get_eulars(int n)
{
phi[1]=1;
for(int i=2;i<=n;i++)
{
if(!st[i])
{
prime[cnt++]=i;
phi[i]=i-1; //i为质数,则与i互质的个数为i-1
}
for(int j=0;prime[j]<=n/i;j++)
{
st[prime[j]*i]=true;
if(i%prime[j]==0)
{
phi[prime[j]*i]=phi[i]*prime[j]; //pi与pj*i的质因子的种类是相同的
break;
}
phi[prime[j]*i]=phi[i]*(prime[j]-1); //pj*pi的质因子种类比pi多一个pj
}
}
LL res=0;
for(int i=1;i<=n;i++) res+=phi[i];
return res;
}
int main()
{
int n;
cin>>n;
cout<<get_eulars(n)<<endl;
return 0;
}
四、快速幂
一、快速幂
给定 n组 ai,bi,pi,对于每组数据,求出 ai^bi mod pi的值。
//O(logn)
typedef long long LL;
LL qmi(int a, int b, int p)
{
LL res = 1 % p;
while (b)
{
if (b & 1) res = res * a % p;
a = a * (LL)a % p;
b >>= 1;
}
return res;
}
二、快速幂求逆元
给定 n 组 ai,pi,其中 pi 是质数,求 ai 模 pi 的乘法逆元,若逆元不存在则输出 impossible。
注意:请返回在 0∼p−1之间的逆元。
乘法逆元的定义
若整数 b,m互质,并且对于任意的整数 a,如果满足 b|a,则存在一个整数 x,使得 a/b≡a×x(mod m),则称 x为 b的模 m 乘法逆元,记为 b^-1(mod m)。
b 存在乘法逆元的充要条件是 b 与模数 m 互质。当模数 m 为质数时,b^m−2 即为 b的乘法逆元。
输入格式
第一行包含整数 n。
接下来 n 行,每行包含一个数组 ai,pi,数据保证 pi是质数。
输出格式
输出共 n 行,每组数据输出一个结果,每个结果占一行。
若 ai模 pi 的乘法逆元存在,则输出一个整数,表示逆元,否则输出 impossible。
数据范围
1≤n≤10^5,
1≤ai,pi≤2∗10^9
输入样例:
3
4 3
8 5
6 3
输出样例:
1
2
impossible
//费马小定理
//b与m互质,则b^m-1 ≡ 1 (mod m)
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
LL qmi(int a, int b, int p)
{
LL res = 1;
while (b)
{
if (b & 1) res = res * a % p;
a = a * (LL)a % p;
b >>= 1;
}
return res;
}
int main()
{
int n;
scanf("%d", &n);
while (n -- )
{
int a, p;
scanf("%d%d", &a, &p);
if (a % p == 0) puts("impossible");
else printf("%lld\n", qmi(a, p - 2, p));
}
return 0;
}
扩展欧几里得
一、扩展欧几里得算法
给定 n 对正整数 ai , bi,对于每对数,求出一组 xi,yi,使其满足 ai×xi+bi×yi=gcd(ai,bi)。
输入格式
第一行包含整数 n。
接下来 n行,每行包含两个整数 ai,bi。
输出格式
输出共 n 行,对于每组 ai,bi,求出一组满足条件的 xi,yi,每组结果占一行。
本题答案不唯一,输出任意满足条件的 xi,yi 均可。
数据范围
1≤n≤10^5,
1≤ai,bi≤2×10^9
输入样例:
2
4 6
8 18
输出样例:
-1 1
-2 1
#include<iostream>
using namespace std;
int exgcd(int a,int b,int &x,int &y)
{
if(!b)
{
x=1,y=0;
return a;
}
int d=exgcd(b,a%b,y,x);
y-=a/b*x;
return d;
}
int main()
{
int n;
cin>>n;
while(n--)
{
int a,b,x,y;
cin>>a>>b;
exgcd(a,b,x,y);
cout<<x<<" "<<y<<endl;
}
return 0;
}
二、线性同余方程
给定 n组数据 ai,bi,mi,对于每组数求出一个 xi,使其满足 ai × xi≡bi (mod mi),如果无解则输出 impossible。
输入格式
第一行包含整数 n。
接下来 n 行,每行包含一组数据 ai,bi,mi。
输出格式
输出共 n 行,每组数据输出一个整数表示一个满足条件的 xi,如果无解则输出 impossible。
每组数据结果占一行,结果可能不唯一,输出任意一个满足条件的结果均可。
输出答案必须在 int 范围之内。
数据范围
1≤n≤105,
1≤ai,bi,mi≤2×109
输入样例:
2
2 3 6
4 3 5
输出样例:
impossible
-3
#include<iostream>
using namespace std;
typedef long long LL;
int exgcd(int a,int b,int &x,int &y)
{
if(b==0)
{
x=1,y=0;
return a;
}
int d=exgcd(b,a%b,y,x);
y-=a/b*x;
return d;
}
int main()
{
int n;
cin>>n;
while(n--)
{
int a,b,m;
cin>>a>>b>>m;
int x,y;
int d=exgcd(a,m,x,y);
if(b%d) puts("impossible");
else cout<<(LL)b/d*x%m<<endl;
}
return 0;
}
高斯消元
一、高斯消元解线性方程组
输入一个包含 n个方程 n 个未知数的线性方程组。
方程组中的系数为实数。
求解这个方程组。
下图为一个包含 m 个方程 n 个未知数的线性方程组示例:
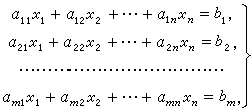
输入格式
第一行包含整数 n。
接下来 n 行,每行包含 n+1 个实数,表示一个方程的 n 个系数以及等号右侧的常数。
输出格式
如果给定线性方程组存在唯一解,则输出共 n 行,其中第 i 行输出第 i 个未知数的解,结果保留两位小数。
如果给定线性方程组存在无数解,则输出 Infinite group solutions。
如果给定线性方程组无解,则输出 No solution。
数据范围
1≤n≤100,
所有输入系数以及常数均保留两位小数,绝对值均不超过 100。
输入样例:
3
1.00 2.00 -1.00 -6.00
2.00 1.00 -3.00 -9.00
-1.00 -1.00 2.00 7.00
输出样例:
1.00
-2.00
3.00
//1.枚举每一列c
//2.找到绝对值最大的一行
//3.将该行交换到最上面
//4.将该行第一个数变成1
//5.将下面的所有行的第c列消成0
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
using namespace std;
const int N=110;
const double eps=1e-6;
double a[N][N];
int n;
int guass()
{
int r,c;
for(r=c=0;c<n;c++)
{
int t=r;
for(int i=r;i<n;i++)
if(fabs(a[i][c])>fabs(a[t][c]))
t=i;
if(fabs(a[t][c])<eps) continue;
for(int i=c;i<n+1;i++) swap(a[t][i],a[r][i]); //交换两行
for(int i=n;i>=c;i--) a[r][i]/=a[r][c]; //将该行第一个数变成1
for(int i=r+1;i<n;i++)
if(fabs(a[i][c])>eps)
for(int j=n;j>=c;j--)
a[i][j]-=a[r][j]*a[i][c]; //将下面的所有行的第c列消成0
r++;
}
if(r<n)
{
for(int i=r;i<n;i++)
if(fabs(a[i][n])>eps) return 2;
return 1;
}
for(int i=n-1;i>=0;i--)
for(int j=i+1;j<n;j++)
a[i][n]-=a[i][j]*a[j][n];
return 0;
}
int main()
{
cin>>n;
for(int i=0;i<n;i++)
for(int j=0;j<n+1;j++)
cin>>a[i][j];
int t=guass();
if(t==0)
{
for(int i=0;i<n;i++) printf("%.2lf\n",a[i][n]);
}
else if(t==1) puts("Infinite group solutions");
else puts("No solution");
return 0;
}
二、高斯消元解异或线性方程组
输入一个包含 n 个方程 n 个未知数的异或线性方程组。
方程组中的系数和常数为 0 或 1,每个未知数的取值也为0或 1。
求解这个方程组。
异或线性方程组示例如下:
M[1][1]x[1] ^ M[1][2]x[2] ^ … ^ M[1][n]x[n] = B[1]
M[2][1]x[1] ^ M[2][2]x[2] ^ … ^ M[2][n]x[n] = B[2]
…
M[n][1]x[1] ^ M[n][2]x[2] ^ … ^ M[n][n]x[n] = B[n]
其中 ^ 表示异或(XOR),M[i] [j]表示第 i个式子中 x[j] 的系数,B[i]是第 ii个方程右端的常数,取值均为 0或 1。
输入格式
第一行包含整数 n。
接下来 n 行,每行包含 n+1 个整数 0或 1,表示一个方程的 n 个系数以及等号右侧的常数。
输出格式
如果给定线性方程组存在唯一解,则输出共 n 行,其中第 i 行输出第 i 个未知数的解。
如果给定线性方程组存在多组解,则输出 Multiple sets of solutions。
如果给定线性方程组无解,则输出 No solution。
数据范围
1≤n≤100
输入样例:
3
1 1 0 1
0 1 1 0
1 0 0 1
输出样例:
1
0
0
#include<iostream>
using namespace std;
const int N=110;
int n;
int a[N][N];
int guass()
{
int r,c;
for(r=c=0;c<n;c++)
{
int t=r;
for(int i=r;i<n;i++)
if(a[i][c])
t=i;
if(!a[t][c]) continue;
for(int i=c;i<n+1;i++) swap(a[t][i],a[r][i]);
for(int i=r+1;i<n;i++)
if(a[i][c])
for(int j=n;j>=c;j--)
a[i][j]^=a[r][j];
r++;
}
if(r<n)
{
for(int i=r;i<n;i++)
if(a[i][n])
return 2;
return 1;
}
for(int i=n-1;i>=0;i--)
for(int j=i+1;j<n;j++)
a[i][n]^=a[i][j]*a[j][n];
return 0;
}
int main()
{
cin>>n;
for(int i=0;i<n;i++)
for(int j=0;j<n+1;j++)
cin>>a[i][j];
int t=guass();
if(t==0)
{
for(int i=0;i<n;i++) cout<<a[i][n]<<endl;
}
else if(t==1) puts("Multiple sets of solutions");
else puts("No solution");
return 0;
}
组合数
一、求组合数 I
// 递推(n^2)
for(int i=0;i<N;i++)
for(int j=0;j<=i;j++)
if(!j) c[i][j]=1;
else c[i][j]=(c[i-1][j]+c[i-1][j-1])%MOD;
二、组合数 II
给定 n 组询问,每组询问给定两个整数 a,b,请你输出 Ca bmod(109+7)的值。
输入格式
第一行包含整数 n。
接下来 n 行,每行包含一组 a 和 b。
输出格式
共 n 行,每行输出一个询问的解。
数据范围
1≤n≤10000,
1≤b≤a≤10^5
输入样例:
3
3 1
5 3
2 2
输出样例:
3
10
1
//预处理/逆元(nlogn)
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 100010, mod = 1e9 + 7;
int fact[N], infact[N];
int qmi(int a, int k, int p)
{
int res = 1;
while (k)
{
if (k & 1) res = (LL)res * a % p;
a = (LL)a * a % p;
k >>= 1;
}
return res;
}
int main()
{
fact[0] = infact[0] = 1;
for (int i = 1; i < N; i ++ )
{
fact[i] = (LL)fact[i - 1] * i % mod;
infact[i] = (LL)infact[i - 1] * qmi(i, mod - 2, mod) % mod;
}
int n;
scanf("%d", &n);
while (n -- )
{
int a, b;
scanf("%d%d", &a, &b);
printf("%d\n", (LL)fact[a] * infact[b] % mod * infact[a - b] % mod);
}
return 0;
}
三、求组合数 III
给定 n组询问,每组询问给定三个整数 a,b,p,其中 p 是质数,请你输出 Ca bmodp 的值。
输入格式
第一行包含整数 n。
接下来 n 行,每行包含一组 a,b,p。
输出格式
共 n 行,每行输出一个询问的解。
数据范围
1≤n≤20,
1≤b≤a≤10^18,
1≤p≤105
输入样例:
3
5 3 7
3 1 5
6 4 13
输出样例:
3
3
2
//卢卡斯定理
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
int qmi(int a, int k, int p)
{
int res = 1;
while (k)
{
if (k & 1) res = (LL)res * a % p;
a = (LL)a * a % p;
k >>= 1;
}
return res;
}
int C(int a, int b, int p)
{
if (b > a) return 0;
int res = 1;
for (int i = 1, j = a; i <= b; i ++, j -- )
{
res = (LL)res * j % p;
res = (LL)res * qmi(i, p - 2, p) % p;
}
return res;
}
int lucas(LL a, LL b, int p)
{
if (a < p && b < p) return C(a, b, p);
return (LL)C(a % p, b % p, p) * lucas(a / p, b / p, p) % p;
}
int main()
{
int n;
cin >> n;
while (n -- )
{
LL a, b;
int p;
cin >> a >> b >> p;
cout << lucas(a, b, p) << endl;
}
return 0;
}
四、求组合数 IV
输入 a,b,求 Ca b的值。
注意结果可能很大,需要使用高精度计算。
输入格式
共一行,包含两个整数 a 和 b。
输出格式
共一行,输出 Ca b的值。
数据范围
1≤b≤a≤5000
输入样例:
5 3
输出样例:
10
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
const int N = 5010;
int primes[N], cnt;
int sum[N];
bool st[N];
void get_primes(int n)
{
for (int i = 2; i <= n; i ++ )
{
if (!st[i]) primes[cnt ++ ] = i;
for (int j = 0; primes[j] <= n / i; j ++ )
{
st[primes[j] * i] = true;
if (i % primes[j] == 0) break;
}
}
}
int get(int n, int p)
{
int res = 0;
while (n)
{
res += n / p;
n /= p;
}
return res;
}
vector<int> mul(vector<int> a, int b)
{
vector<int> c;
int t = 0;
for (int i = 0; i < a.size(); i ++ )
{
t += a[i] * b;
c.push_back(t % 10);
t /= 10;
}
while (t)
{
c.push_back(t % 10);
t /= 10;
}
return c;
}
int main()
{
int a, b;
cin >> a >> b;
get_primes(a);
for (int i = 0; i < cnt; i ++ )
{
int p = primes[i];
sum[i] = get(a, p) - get(a - b, p) - get(b, p);
}
vector<int> res;
res.push_back(1);
for (int i = 0; i < cnt; i ++ )
for (int j = 0; j < sum[i]; j ++ )
res = mul(res, primes[i]);
for (int i = res.size() - 1; i >= 0; i -- ) printf("%d", res[i]);
puts("");
return 0;
}
五、卡特兰数
给定 n 个 0 和 n 个 1,它们将按照某种顺序排成长度为 2n 的序列,求它们能排列成的所有序列中,能够满足任意前缀序列中 0 的个数都不少于 1 的个数的序列有多少个。
输出的答案对 109+7 取模。
输入格式
共一行,包含整数 n。
输出格式
共一行,包含一个整数,表示答案。
数据范围
1≤n≤10^5
输入样例:
3
输出样例:
5
#include<iostream>
using namespace std;
const int MOD=1e9+7;
typedef long long LL;
int qmi(int a,int k,int p)
{
int res=1;
while(k)
{
if(k&1) res=(LL)res*a%MOD;
a=(LL)a*a%MOD;
k>>=1;
}
return res;
}
int main()
{
int n;
cin>>n;
int res=1;
for(int i=2*n;i>n;i--) res=(LL)res*i%MOD;
for(int i=1;i<=n;i++) res=(LL)res*qmi(i,MOD-2,MOD)%MOD;
res=(LL)res*qmi(n+1,MOD-2,MOD)%MOD;
cout<<res<<endl;
return 0;
}
容斥原理
给定一个整数 n 和 m 个不同的质数 p1,p2,…,pm。
请你求出 1∼n中能被 p1,p2,…,pm中的至少一个数整除的整数有多少个。
输入格式
第一行包含整数 n 和 m。
第二行包含 m 个质数。
输出格式
输出一个整数,表示满足条件的整数的个数。
数据范围
1≤m≤16
1≤n,pi≤10^9
输入样例:
10 2
2 3
输出样例:
7
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 20;
int p[N];
int main()
{
int n, m;
cin >> n >> m;
for (int i = 0; i < m; i ++ ) cin >> p[i];
int res = 0;
for (int i = 1; i < 1 << m; i ++ )
{
int t = 1, s = 0;
for (int j = 0; j < m; j ++ )
if (i >> j & 1)
{
if ((LL)t * p[j] > n)
{
t = -1;
break;
}
t *= p[j];
s ++ ;
}
if (t != -1)
{
if (s % 2) res += n / t;
else res -= n / t;
}
}
cout << res << endl;
return 0;
}