1. 概述
XGBoost本身的核心是基于梯度提升树实现的集成算法,整体来说可以有三个核心部分:集成算法本身,用于集成的弱评估器,以及应用中的其他过程。
1.1 提升集成算法:
XGBoost的基础是梯度提升算法,因此我们必须先从了解梯度提升算法开始。梯度提升(Gradient boosting)是构建预测模型的最强大技术之一,它是集成算法中提升法(Boosting)的代表算法。集成算法通过在数据上构建多个弱评估器,汇总所有弱评估器的建模结果,以获取比单个模型更好的回归或分类表现。
集成不同弱评估器的方法有很多种。有像我们曾经在随机森林的课中介绍的,一次性建立多个平行独立的弱评估器的装袋法。也有像我们今天要介绍的提升法这样,逐一构建弱评估器,经过多次迭代逐渐累积多个弱评估器的方法。提升法的中最著名的算法包括Adaboost和梯度提升树,XGBoost就是由梯度提升树发展而来的。梯度提升树中可以有回归树也可以有分类树,两者都以CART树算法作为主流,XGBoost背后也是CART树,这意味着XGBoost中所有的树都是二叉的。
XGB vs GBDT 核心区别1:求解预测值 的方式不同
GBDT中预测值是由所有弱分类器上的预测结果的加权求和,其中每个样本上的预测结果就是样本所在的叶子节点的均值。而XGBT中的预测值是所有弱分类器上的叶子权重直接求和得到,计算叶子权重是一个复杂的过程。

1.2简单建模测试
from xgboost import XGBRegressor as XGBR
from sklearn.ensemble import RandomForestRegressor as RFR
from sklearn.linear_model import LinearRegression as LinearR
from sklearn.datasets import load_boston#用于回归的数据集
from sklearn.model_selection import KFold, cross_val_score as CVS, train_test_split as TTS
from sklearn.metrics import mean_squared_error as MSE
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from time import time
import datetime
#加载数据集信息
data = load_boston()
#波士顿数据集非常简单,但它所涉及到的问题却很多
X = data.data
y = data.target
print(X.shape)
print(y.shape)
#划分数据集信息
Xtrain,Xtest,Ytrain,Ytest = TTS(X,y,test_size=0.3,random_state=420)
reg = XGBR(n_estimators=100).fit(Xtrain,Ytrain) #训练
reg.predict(Xtest) #传统接口predict
R2 = reg.score(Xtest,Ytest) #你能想出这里应该返回什么模型评估指标么?利用shift+Tab可以知道,R^2评估指标
print('R2',R2)
print(y.mean())#输出y的平均值,
MSE_score = MSE(Ytest,reg.predict(Xtest))#可以看出均方误差是平均值y.mean()的1/3左右,结果不算好也不算坏
print('MSE_score',MSE_score)
#可以查看到模型特征的贡献数
feature_im = reg.feature_importances_ #树模型的优势之一:能够查看模型的重要性分数,可以使用嵌入法(SelectFromModel)进行特征选择
#xgboost可以使用嵌入法进行特征选择
reg = XGBR(n_estimators=100) #交叉验证中导入的没有经过训练的模型
cvs_socre = CVS(reg,Xtrain,Ytrain,cv=5).mean()
#这里应该返回什么模型评估指标,还记得么? 返回的是与reg.score相同的评估指标R^2(回归),准确率(分类)
print('cvs_socre',cvs_socre)
cvs_mse = CVS(reg,Xtrain,Ytrain,cv=5,scoring='neg_mean_squared_error').mean()
#查看sklearn总所有的模型评估指标
import sklearn
print(sorted(sklearn.metrics.SCORERS.keys()))
#使用随机森林和线性回归进行一个对比
rfr = RFR(n_estimators=100)#随机森林模型
cvs_socre_r2 = CVS(rfr,Xtrain,Ytrain,cv=5).mean()#0.7975497480638329
CVS(rfr,Xtrain,Ytrain,cv=5,scoring='neg_mean_squared_error').mean()#-16.998723616338033
lr = LinearR()#线性回归模型
CVS(lr,Xtrain,Ytrain,cv=5).mean()#0.6835070597278085
CVS(lr,Xtrain,Ytrain,cv=5,scoring='neg_mean_squared_error').mean()#-25.34950749364844
#如果开启参数slient:在数据巨大,预料到算法运行会非常缓慢的时候可以使用这个参数来监控模型的训练进度
reg = XGBR(n_estimators=10,silent=True)#xgboost库silent=True不会打印训练进程,只返回运行结果,默认是False会打印训练进程
#sklearn库中的xgbsoost的默认为silent=True不会打印训练进程,想打印需要手动设置为False
CVS(reg,Xtrain,Ytrain,cv=5,scoring='neg_mean_squared_error').mean()#-92.67865836936579
def plot_learning_curve(estimator, title, X, y,
ax=None, # 选择子图
ylim=None, # 设置纵坐标的取值范围
cv=None, # 交叉验证
n_jobs=None # 设定索要使用的线程
):
from sklearn.model_selection import learning_curve
import matplotlib.pyplot as plt
import numpy as np
train_sizes, train_scores, test_scores = learning_curve(estimator, X, y
, shuffle=True
, cv=cv
, random_state=420
, n_jobs=n_jobs)
if ax == None:
ax = plt.gca()
else:
ax = plt.figure()
ax.set_title(title)
if ylim is not None:
ax.set_ylim(*ylim)
ax.set_xlabel("Training examples")
ax.set_ylabel("Score")
ax.grid() # 绘制网格,不是必须
ax.plot(train_sizes, np.mean(train_scores, axis=1), 'o-'
, color="r", label="Training score")
ax.plot(train_sizes, np.mean(test_scores, axis=1), 'o-'
, color="g", label="Test score")
ax.legend(loc="best")
return ax
cv = KFold(n_splits=5, shuffle = True, random_state=42) #交叉验证模式
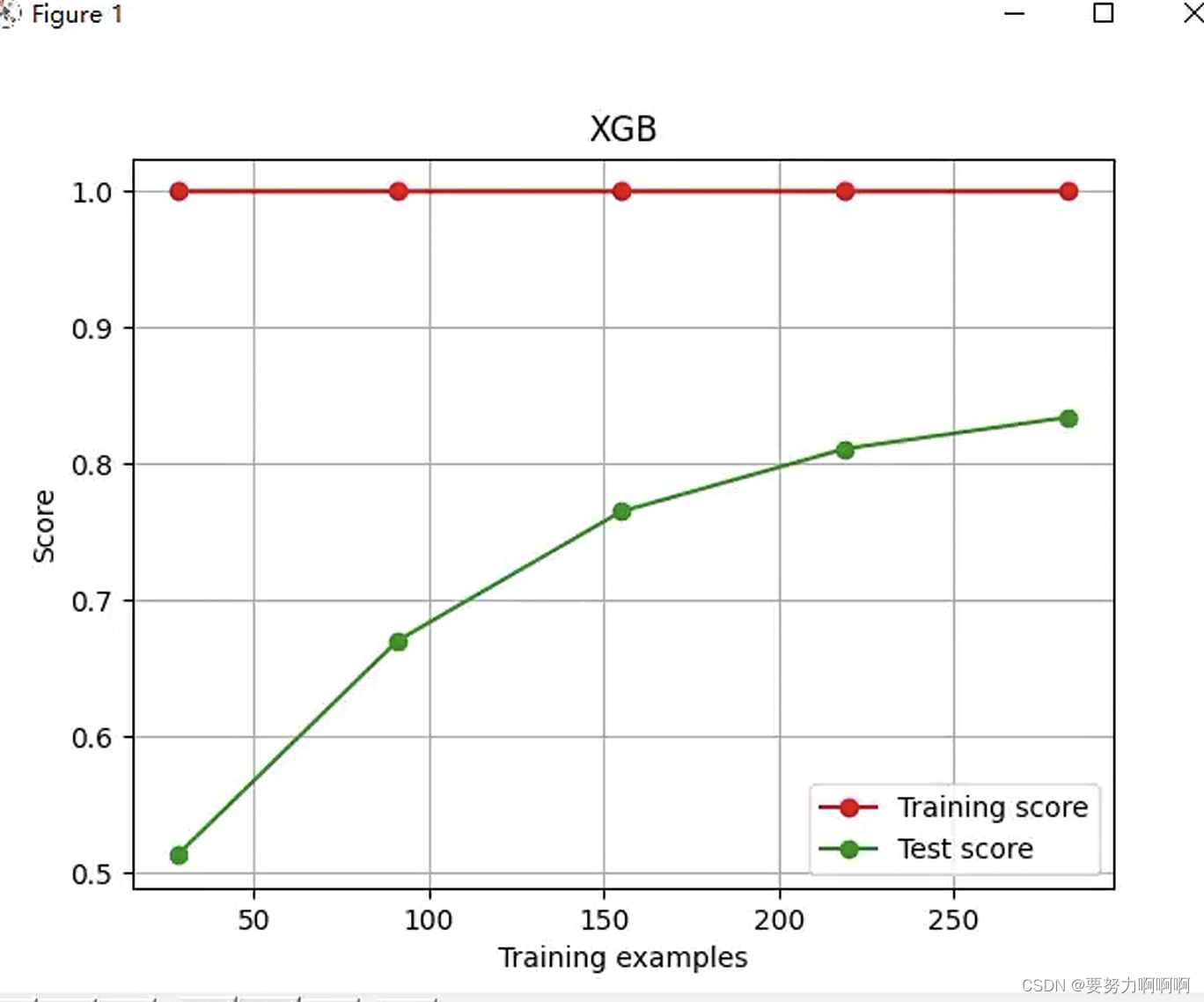
plot_learning_curve(XGBR(n_estimators=100,random_state=420)
,"XGB",Xtrain,Ytrain,ax=None,cv=cv)
plt.show()
#=====【TIME WARNING:25 seconds】=====#
axisx = range(10,1010,50)
rs = []
for i in axisx:
reg = XGBR(n_estimators=i,random_state=420)#也就是说,当n_estimators的时候,XGBR得到最好的结果。
rs.append(CVS(reg,Xtrain,Ytrain,cv=cv).mean())#R2取值最大的时候的K
print(axisx[rs.index(max(rs))],max(rs))
plt.figure(figsize=(20,5))
plt.plot(axisx,rs,c="red",label="XGB")
plt.legend()
plt.show()
1.3有放回随机抽样:
建立了众多的树,怎么就能够保证模型整体的效果变强呢?集成的目的是为了模型在样本上能表现出更好的效果,所以对于所有的提升集成算法,每构建一个评估器,集成模型的效果都
会比之前更好。也就是随着迭代的进行,模型整体的效果必须要逐渐提升,最后要实现集成模型的效果最优。
我们训练模型之前,必然会有一个巨大的数据集。我们都知道树模型是天生过拟合的模型,并且如果数据量太过巨大,树模型的计算会非常缓慢,因此,我们要对我们的原始数据集进行有放回抽样(bootstrap)。有放回的抽样每次只能抽取一个样本,若我们需要总共N个样本,就需要抽取N次。每次抽取一个样本的过程是独立的,这一次被抽到的样本会被放回数据集中,下一次还可能被抽到,因此抽出的数据集中,可能有一些重复的数据。
在梯度提升树中,我们每一次迭代都要建立一棵新的树,因此我们每次迭代中,都要有放回抽取一个新的训练样本。不过,这并不能保证每次建新树后,集成的效果都比之前要好。因此我们规定,在梯度提升树中,每构建一个评估器,都让模型更加集中于数据集中容易被判错的那些样本。
首先我们有一个巨大的数据集,在建第一棵树时,我们对数据进行初次又放回抽样,然后建模。建模完毕后,我们对模型进行一个评估,然后将模型预测错误的样本反馈给我们的数据集,一次迭代就算完成。紧接着,我们要建立第二棵决策树,于是开始进行第二次又放回抽样。但这次有放回抽样,和初次的随机有放回抽样就不同了,在这次的抽样中,我们加大了被第一棵树判断错误的样本的权重。