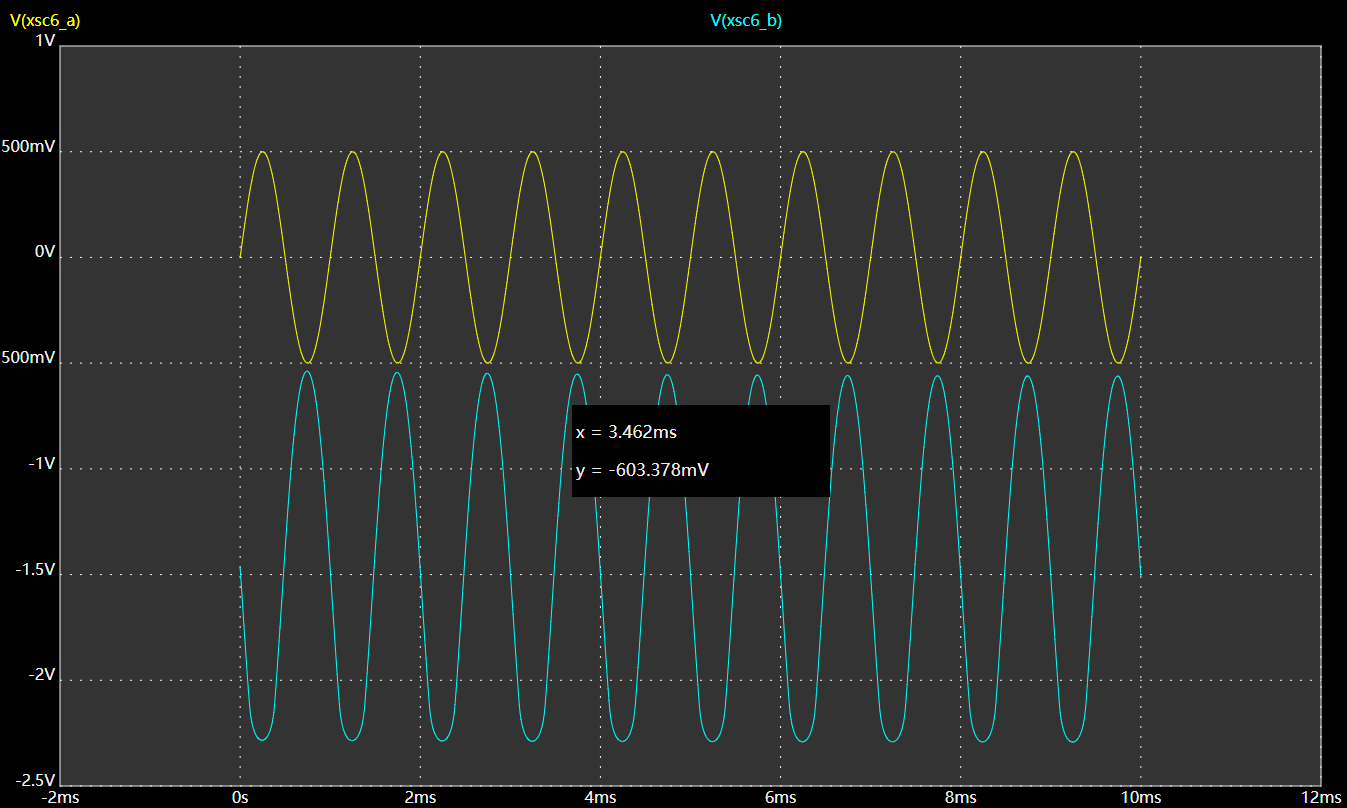
积分的积分区域及被积表达式

重点：积分的结果均为数值，仅与被积表达式和积分区间有关！！！

1.如何一下子区分一重积分，二重积分，三重积分？

看积分区间和被积表达式：
一重积分积分区间是长度，一段长度，被积表达式是关于x的函数。
二重积分积分区间是区域，一片区域，被积表达式是关于x,y的函数。
三重积分积分区间是空间，一块空间，被积表达式是关于x,y,z的函数。

2.一重积分（定积分）

一重积分积分区域是一段长度，对1积分就是一段线的长度。 被积表达式就是常见的初等函数。

一重积分的基础应用（本职工作）：
可以用于求平面面积，曲线弧长（这个弧长积分是平面上的x,y轴，后面的第一类曲线积分是三维的x,y,z不要弄混，当然后者相当于前者升维）

一重积分的特殊应用，拓展业务（可以做二重积分，曲面积分做的事）：
可用于求旋转体体积，旋转体侧面积。

注：这里只是看似相当于二重积分和曲面积分的应用，实质上还是一重积分的方法（积分区间和被积表达式本质没有改变，还是一段长度和关于x的函数）。之所以可以求是因为旋转体体积是规则的，某个面积公式是知道的，所以我们可以让无数个面积叠加，叠加长度就是区间长度。

用一重积分求旋转体体积：
如下面这个：对πr^2叠加，叠加长度为区间长度。叠加面积半径f(x)求出

用二重积分求旋转体体积：
可以看到如果二重积分求，那本质就改变了，积分区域变成了区域Dxy,被积函数变成了关于x,y的函数也就是r(x,y)

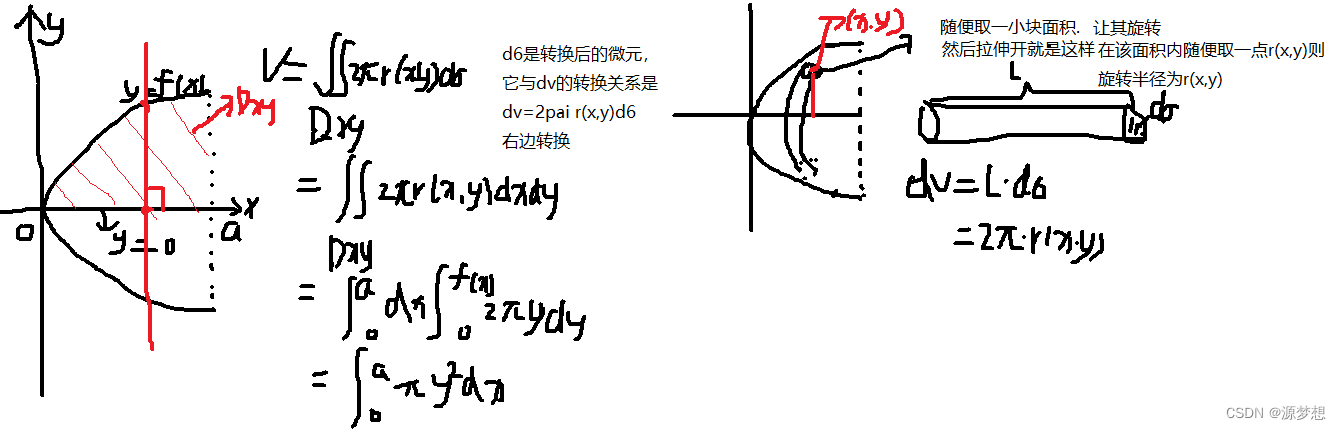
3.二重积分

二重积分积分区域是一片区域，对1积分就是区域的面积。

二重积分的基础应用：
求不规则，规则体积，质心，形心，质量，转动惯量等
在二重积分计算中一般只关注积分区域D如何转换成X，Y型，极坐标，
在三重积分计算中比较关注求体积问题
没有讲扩展业务

4.三重积分

三重积分积分区域是一块空间，对1积分就是空间体积。

三重积分的应用：
求体积，质量，质心，形心，转动惯量等
扩展：若三重积分求几何度量，那就是四维几何意义。
没有讲扩展业务

5.二重积分，三重积分为何不能直接带入积分区域？

如下场景1：∭x²+y²+z²dv. 积分空间为欧米噶为x²+y²+z²<=1
哎，你看我这样原式=∭1dv = 圆的体积 做完了。（错^N>一个亿）

如下场景2：∬x²+y²dσ. 积分区域为D：x²+y²=R².
哎，你看看，原式=∬R²dσ=R²∬1dσ=R²x圆的面积 做完了，完全没有难度。

以上两个场景大错特错，为何呢？
结论：二重积分，三重积分不可以 将积分区域,空间的不等式， 当作等式带入被积表达式。
错误1：不等式怎么能变成等式带入呢？

错误2：二三重积分的区域都是一个范围，且在该范围不同地方被积表达式式变化的（也就是说被积表达式是一个变量），等式带入，相当于将被积表达式钉死在范围边界成立的地方，即无论在范围哪个地方，都是边界成立时的被积表达式。

错误3：根据积分定理，积分是一个数值，仅与被积函数和积分区间有关，将等式带入，相当于改变了被积表达式，不是原来的积分了。

6.什么情况下能直接带入积分区域？

1.一重积分（定积分）
定积分可以带入，但是一般不会给出被积表达式的等式，都是直接给出被积表达式

2.二类曲面积使用高斯公式转换前可以带入
转换之前可以带入：因为对曲面积分，积分区域时曲面，曲面是由无数个点组成的，这无数个点在曲面表达式都是成立的，故可以直接带入。

转换之后不能带入：高斯公式之后，积分区域由曲面变成曲面所围成的空间，这时候，这无数个点不仅仅时曲面上等式成立的点，还包含曲面所围成的空间里面等式不成立的点，故不能带入。

3.二类曲线积分使用格林公式前可以带入
同理：
转换之前：曲线上无数个点，在曲线方程等式都成立，可以带入。
转换之后：积分区间：由线变成线所包含的域，在线内部点曲线方程等式不成立。

3.二类空间曲线积分使用斯托克斯公式之前可以带入
斯托克斯公式可以将三维曲线积分转成第一，二类曲面积分
转换之后，积分区域由线变成面，曲线方程只有在边界成立，故不可以带入。
当然如果转换之后的曲面方程可以表示出来，曲面方程是可以直接带入的。