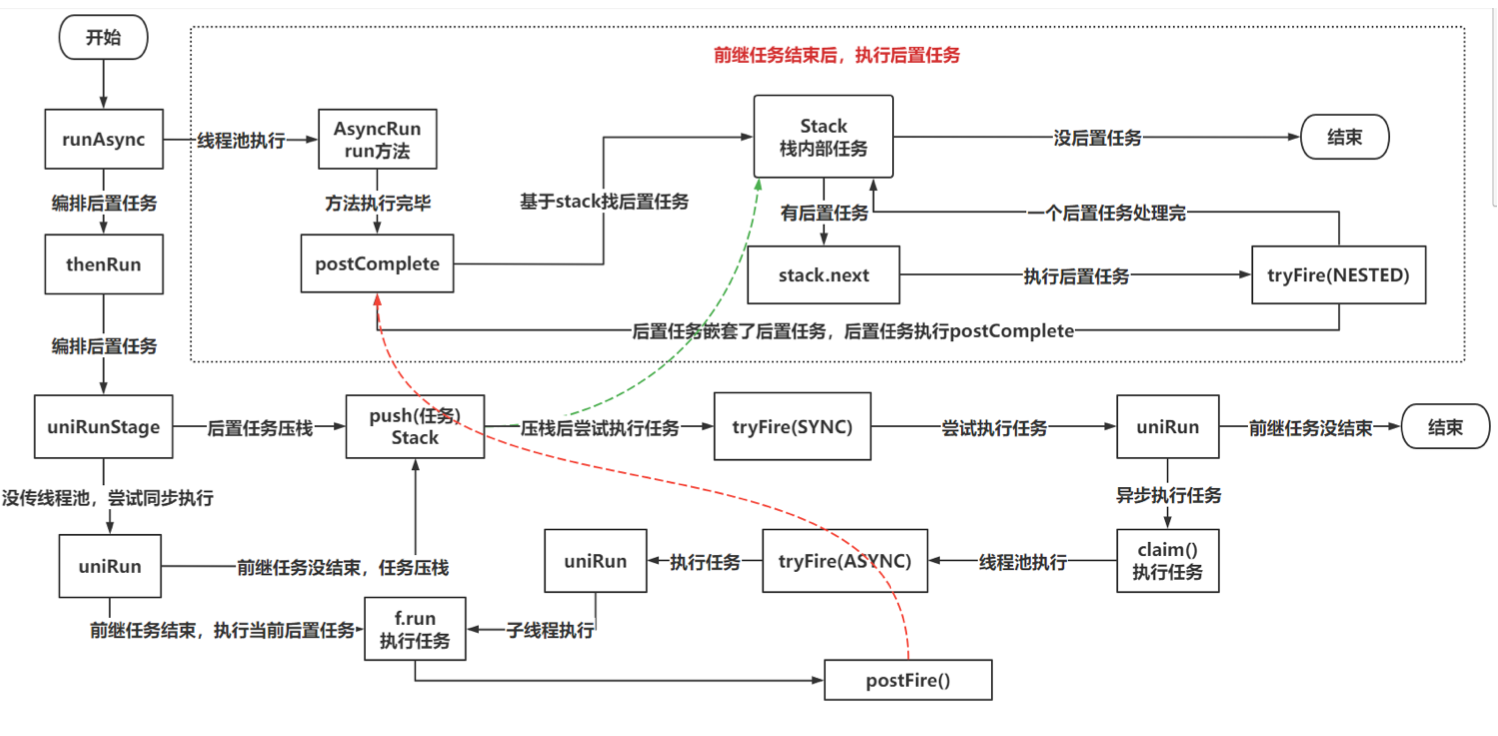
排序算法稳定性

假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次序保持不变，即在原序列中，r[i]=r[j]，且r[i]在r[j]之前，而在排序后的序列中，r[i]仍在r[j]之前，则称这种排序算法是稳定的；否则称为不稳定的。

冒泡排序（bubble sort）

列表中每相邻的两个数进行比较，如果前面比后面大，则交换这两个数。

一趟排序完成后，无序区减少了一个数，有序区增加了一个数。

代码关键点：总趟数（n-1），每一趟无序区范围,每一趟下标最大值为(n-i-1)

代码关键点分析：

总趟数（n-1）

无序列表：arr[n] = {val0, val1, ..., val(n-1)};

n = 1时，即无序列表只有1个元素，只要进行比较0趟

n = 2 时，即无序列表有2个元素，只要进行比较1趟

n = 3 时，即无序列表有3个元素，只要进行比较2趟

n = n 时，即无序列表有n个元素，只要进行比较 n - 1 趟

每一趟下标最大值为(n-i-1)

n = 3 时，即无序列表有3个元素，只要进行比较2趟，趟数从0开始，那么第0趟下标的最大值为n-i-1即3-0-1 = 2；

代码：

#include <iostream>

using namespace std;

template<typename T>
void bubble_sort(T *arr, int n)
{
    T temp;
    bool exchange;

    for (int i = 0; i < n-1; i++) //总趟数：n-1
    {
        exchange = false;
        for (int j = 0; j < n-i-1; j++) //每一趟下标最大值（即j+1这个下标的最大值）为：n-i-1
        {
            if (arr[j] > arr[j+1])
            {
                temp = arr[j];
                arr[j] = arr[j+1];
                arr[j+1] = temp;
                
                exchange = true;
            }
        }

        if (!exchange) //一趟中，没有发生任何元素的交换，说明列表已排好序
            break;
    }
}

int main(int argc, char *argv[])
{
    int arr[] = {3,5,2,1,4};
    int n = sizeof(arr)/sizeof(*arr);
    
    cout << "---before bubble sort---" << endl;
    for (int i = 0; i < n; i++)
    {
            cout << arr[i] << " ";
    }
    cout << endl;

    bubble_sort(arr, n);
    cout << "---after bubble sort---" << endl;
    for (int i = 0; i < n; i++)
    {
            cout << arr[i] << " ";
    }
    cout << endl;

    return 0;
}

结果：