引言

从本节开始，将介绍狄利克雷过程。

回顾：高斯混合模型

高斯混合模型( $\text{Gaussian Mixture Model,GMM}$ )是针对无监督学习中聚类任务的混合模型。
基于 $N$ 个样本的样本集合 $\mathcal X = \{x^{(i)}\}_{i=1}^N$ ，关于模型参数 $\theta$ 的学习过程，使用的底层逻辑是极大似然估计( $\text{Maximum Likelihood Estimate,MLE}$ )：
$\mathop{\arg\max}\limits_{\theta} \left[\log \mathcal P(\mathcal X)\right] = \mathop{\arg\max}\limits_{\theta} \left[\sum_{i=1}^N \log \sum_{k=1}^{\mathcal K} \alpha_{k} \cdot \mathcal N(x^{(i)} \mid \mu_k,\Sigma_{k})\right]$
它的模型参数 $\theta$ 具体包含三个部分：
当然， $\alpha$ 一共包含 $\mathcal K$ 个离散信息，但如果求解出 $\alpha_1,\cdots,\alpha_{\mathcal K-1}$ ,那么最后一个 $\alpha_{\mathcal K} = 1 - (\alpha_1 + \cdots + \alpha_{\mathcal K - 1})$ 即可。
$\theta = \{\mu_1,\cdots,\mu_{\mathcal K},\Sigma_1,\cdots,\Sigma_{\mathcal K},\alpha_1,\cdots,\alpha_{\mathcal K-1}\}$
关于高斯混合模型的概率图结构表示如下：
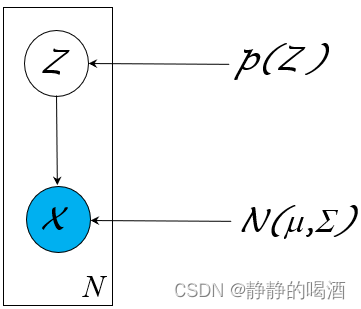
高斯混合模型——概率图结构
由于概率图结构简单，并且 $\mathcal Z$ 是一维的、离散型随机变量； $\mathcal X \mid \mathcal Z$ 服从高斯分布，因而该模型是特殊的、直接使用 $\text{EM}$ 算法就可求解模型参数的模型结构。

狄利克雷过程——引出

关于某一个聚类任务，如果集合 $\mathcal X$ 在样本空间中的分布结构简单、易于观察聚类数量，我们可以轻易地定义聚类数量 $\mathcal K$ 的取值；

但如果处于某些原因，导致样本空间中的样本分布无法容易地观察出来。如：

样本数量较少；
聚类情况过于琐碎，聚类效果不明显；
样本的特征维度过高，导致无法通过观察得到样本的聚类数量。

这导致我们没有办法确定聚类数量 $\mathcal K$ 。一种想法是：如果将聚类数量 $\mathcal K$ 也作为模型参数 $\theta$ 的一部分：
$\theta' = \{\mu_1,\cdots,\mu_{\mathcal K},\Sigma_1,\cdots,\Sigma_{\mathcal K},\alpha_1,\cdots,\alpha_{\mathcal K-1},\mathcal K\}$

从而使用极大似然估计去求解 $\mathcal K$ 。但真实情况下，这种方式可能是不可取的。我们首先观察对数似然函数 $\log \mathcal P(\mathcal X)$ ：
$\log \mathcal P(\mathcal X) = \sum_{i=1}^N \log \sum_{k=1}^{\mathcal K} \alpha_{k} \cdot \mathcal N(x^{(i)} \mid \mu_k,\Sigma_k)$
连加项中的核心构成是由聚类概率 $\alpha_k$ 与对应高斯分布的概率密度函数 $\mathcal N(\mu_k,\Sigma_k)$ 构成。可能出现如下情况：

当 $\mathcal K = N$ 时，即任意一个样本自身归为一类。那么某样本在基于该样本产生的高斯分布中，对应的概率密度函数结果一定是最大值。如果样本数量较少， $\alpha_{k}(k=1,2,\cdots,\mathcal K)$ 没有被划分的过于细碎，最终这种方法对应的 $\log \mathcal P(\mathcal X)$ 可能会脱颖而出。

这种做法所划分出来的聚类结果，对于聚类任务来说是没有意义的。

针对这种聚类模糊的样本分布，我们可以尝试：

针对每一个样本 $x^{(i)}(i=1,2,\cdots,N)$ 构建一个对应的参数 $\theta^{(i)}(i=1,2,\cdots,N)$ ；
其中 $\theta^{(i)}(i=1,2,\cdots,N)$ 的具体意义依然是描述对应样本 $x^{(i)}(i=1,2,\cdots,N)$ 的聚类信息;只不过 $\theta^{(i)}$ 仅仅对 $x^{(i)}$ 一个样本负责。
此时，已经有了 $N$ 个参数 $\theta$ ，对于每一个参数 $\theta^{(i)}$ ，它均会服从某个分布 $\mathcal H(\theta)$ ：
$\theta^{(i)} \sim \mathcal H(\theta) \quad i=1,2,\cdots,N$
需要对分布 $\mathcal H(\theta)$ 进行限制，假设 $\mathcal H(\theta)$ 是一个连续分布( $\text{Continuous Distribution}$ )，那会出现什么样的情况？

假设各样本之间独立同分布( $\text{Independent Identical Distribution,IID}$ )，并且样本之间不存在重复。对于数据集合中任意两个样本 $x^{(i)},x^{(j)} \in \mathcal X$ ，其对应的 $\theta^{(i)},\theta^{(j)}$ 不相同的概率无限接近于 $0$ 。这导致的直接后果是：任意两个样本对应的概率分布均不相同。
$\theta^{(i)},\theta^{(j)} \sim \mathcal H(\theta) \Rightarrow \mathcal P(\theta^{(i)} = \theta^{(j)}) = 0$

此时又回到了上面的问题：每个样本的分布均不相同，意味着 $\mathcal K = N$ 。这样的聚类结果自然没有意义。
但实际上，由于样本 $x^{(i)}$ 之间的差异性，对应参数 $\theta^{(i)}$ 之间同样存在差异。因而 $\mathcal H(\theta)$ 确实是一个关于 $\theta$ 的连续分布。但因为上面的问题，不能从 $\mathcal H(\theta)$ 中直接采样。因而需要找到一个和 $\mathcal H(\theta)$ 相似的离散分布。该离散分布记作 $\mathcal G$ ，具体表示如下：
$\mathcal G \sim \text{DP}(\alpha,\mathcal H)$

其中 $\text{DP}$ 是指狄利克雷过程( $\text{Dirichlet Process,DP}$ )； $\alpha$ 表示产生分布 $\mathcal G$ 离散型程度的标量( $\text{Scalar}$ )参数：
$\alpha$ 自身是一个大于 $0$ 的标量。

如果 $\alpha$ 的数值越大，通过狄利克雷过程 $\text{DP}(\alpha,\mathcal H)$ 产生的分布 $\mathcal G$ 越不离散。

一个分布越离散是指该分布对特征选择的种类越少。最离散的效果就是分布对某种类别选择的概率是1，没有其他选择。
相反，越不离散是指该分布对特征选择的种类很多，对每一个种类的选择均有相应的概率结果。如果 $\alpha$ 的取值是无穷大，那么该分布就变成了连续分布 $\mathcal H(\theta)$ 。
相反， $\alpha$ 的数值很小，那么产生的分布 $\mathcal G$ 会非常的离散。

举个例子。下图的蓝色点表示关于 $\mathcal H(\theta)$ 的二维高斯分布：
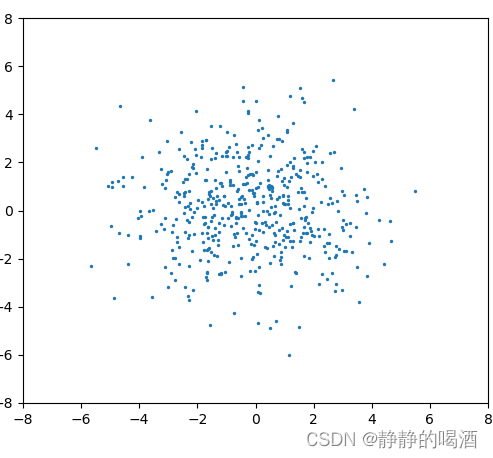
二维高斯分布——示例
这明显是一个连续型分布。我们想通过狄利克雷过程 $\text{DP}(\alpha,\mathcal H)$ 去构建一个离散分布 $\mathcal G$ ，使 $\mathcal G$ 能够近似分布 $\mathcal H$ 。

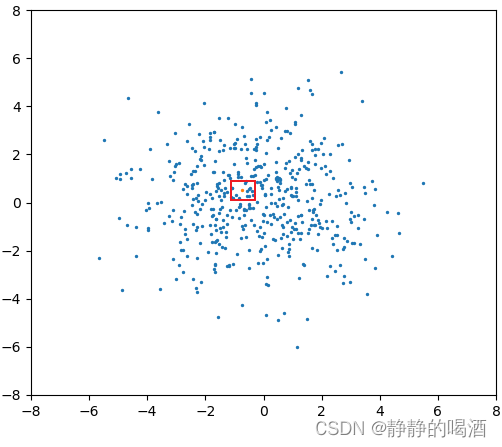
根据上面的描述，如果 $\alpha$ 取值为 $0$ ，产生 $\mathcal G$ 分布的样本点表示如下(橙色点)：
此时属于‘最离散的状态’,无论怎样去随机采样，最终得到的只有一种选取结果，红色框标注。
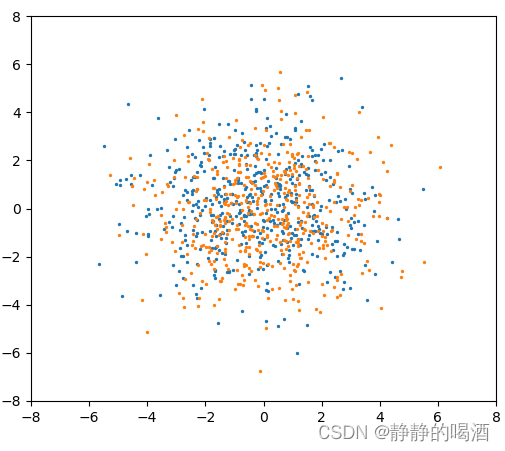
相反，如果 $\alpha$ 的取值足够高，对应产生 $\mathcal G$ 分布的样本点表示如下(依然是橙色点)：
此时，它的离散分布状态足够多，每种状态都能分到对应的概率结果，当 $\alpha \Rightarrow \infty$ 时，此时的离散分布 $\mathcal G$ 等于连续分布 $\mathcal H$ 。

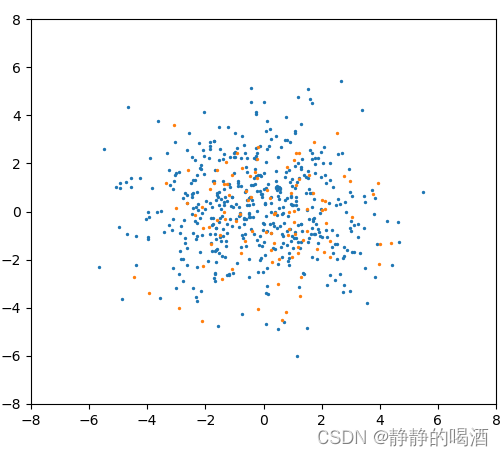
当然，无论是上述哪种极端情况，都是不可取的：

如果样本分布过于离散，就如上述一个橙色样本表示整个概率分布一样，那么样本分布表达的准确性是较差的；
相反，如果样本更偏于连续，产生的分布可能会产生过拟合的现象，并且对于采样过程也存在较大的负担。
因而我们需要一个尽可能地将分布 $\mathcal H$ 的信息表示出来的离散分布(效果图)：

相关参考：
徐亦达机器学习：Dirichlet Process Part 1