本文属于「征服LeetCode」系列文章之一，这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁，本系列将至少持续到刷完所有无锁题之日为止；由于LeetCode还在不断地创建新题，本系列的终止日期可能是永远。在这一系列刷题文章中，我不仅会讲解多种解题思路及其优化，还会用多种编程语言实现题解，涉及到通用解法时更将归纳总结出相应的算法模板。

为了方便在PC上运行调试、分享代码文件，我还建立了相关的仓库。在这一仓库中，你不仅可以看到LeetCode原题链接、题解代码、题解文章链接、同类题目归纳、通用解法总结等，还可以看到原题出现频率和相关企业等重要信息。如果有其他优选题解，还可以一同分享给他人。

由于本系列文章的内容随时可能发生更新变动，欢迎关注和收藏征服LeetCode系列文章目录一文以作备忘。

Given a callable function f(x, y) with a hidden formula and a value z, reverse engineer the formula and return all positive integer pairs x and y where f(x,y) == z. You may return the pairs in any order.

While the exact formula is hidden, the function is monotonically increasing, i.e.:

• f(x, y) < f(x + 1, y)
• f(x, y) < f(x, y + 1)

The function interface is defined like this:

interface CustomFunction {
public:
  // Returns some positive integer f(x, y) for two positive integers x and y based on a formula.
  int f(int x, int y);
};

We will judge your solution as follows:

• The judge has a list of 9 hidden implementations of CustomFunction, along with a way to generate an answer key of all valid pairs for a specific z.
• The judge will receive two inputs: a function_id (to determine which implementation to test your code with), and the target z.
• The judge will call your findSolution and compare your results with the answer key.
• If your results match the answer key, your solution will be Accepted.

题意：给你一个函数  f(x, y) 和一个目标结果 z，函数公式未知，计算方程 f(x,y) == z 所有可能的正整数 数对 x 和 y。满足条件的结果数对可以按任意顺序返回。尽管函数的具体式子未知，但它是单调递增函数，也就是说：

• f(x, y) < f(x + 1, y)
• f(x, y) < f(x, y + 1)

---

解法1 双重循环

由于数据不大，可以直接暴力循环。

• 时间复杂度：$O(n^2)$
• 空间复杂度：$O(1)$

class Solution {
public:
    vector<vector<int>> findSolution(CustomFunction& customfunction, int z) {
        vector<vector<int>> ans;
        for (int x = 1; x <= 1000; ++x) {
            for (int y = 1; y <= 1000; ++y) {
                if (customfunction.f(x, y) == z) ans.push_back({x, y});
            }
        }
        return ans;
    }
};

---

解法2 二分

类似LeetCode 15 三数之和，循环遍历 $x$ ，然后对单调递增的 $y$ 进行二分搜索。

• 时间复杂度：$O(n\log n)$ 。
• 空间复杂度：$O(1)$

class Solution {
public:
    vector<vector<int>> findSolution(CustomFunction& customfunction, int z) {
        vector<vector<int>> ans;
        for (int x = 1; x <= 1000; ++x) {
            int yl = 1, yh = 1000;
            while (yl <= yh) {
                int mid = (yl + yh) / 2, tz = customfunction.f(x, mid);
                if (tz == z) {
                    ans.push_back({x, mid});
                    break;
                } 
                else if (tz > z) yh = mid - 1; // 说明y太大了
                else yl = mid + 1;
            }
        }
        return ans;
    }
};

---

解法3 抽象BST

官解告诉我们这是240题搜索二维矩阵II的变形题，如果题目读不懂，不妨看看本题前身240题搜索二维矩阵II是一道怎样的题目——这道题的题目含义就非常清晰了。最关键的信息在于，对于给定的 $m\times n$ 矩阵 matrix ，存在以下性质：

• 每行的元素从左到右升序排列
• 每列的元素从上到下升序排列

用数学语言来表达的话，就是对于下标为 $(x,y)$ 的元素 $matrix[x][y]$ ，（在不越界的情况下）一定存在以下两个关系：

• $matrix[x][y]<matrix[x][y+1]$ ，即同一行的元素从左往右单调递增
• $matrix[x][y]<matrix[x+1][y]$ ，即同一列的元素从上往下单调递增
  
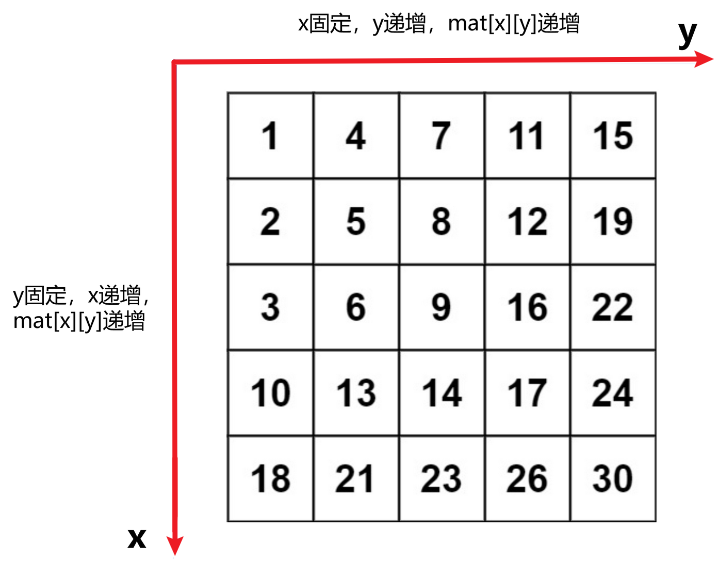
  我们对240题的搜索过程如下所示：
  
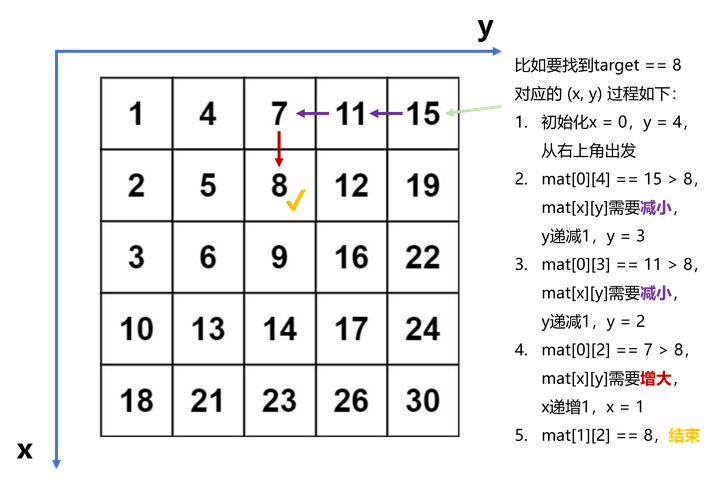
  如果我们把整个矩阵 matrix 看作是一棵二叉树，每一个值都是一个节点，把起始点 $(0,n-1)$ 看作根节点，左边的值看作是左节点，下面的值看作是右节点，那么这个二维矩阵可以抽象成一颗二叉搜索树BST。我们的搜寻过程，其实也遵循BST的搜索原则。

从而对于本题，我们也可以这么做：

1. 把解也就是 x 和 y 类似上图一样，看做一个二维矩阵，高宽均是1000（取值范围）
2. 从二维数组右上角开始，即 $x=1,y=1000$ 为起始点，将这个起始点看为二叉搜索树的根节点
3. 由于函数方程具有单调性，也就是任一点向左 $(y-1)$ 结果递减，任一点向下 $(x+1)$ 结果递增
4. 从起始点来看，向左对应二叉搜索树的左子结点，向下对应二叉搜索树的右子结点
5. 从起始点逐个得到当前 $x$ 和 $y$ 的方程结果，比目标值大则向左移动，比目标值小则向下移动
6. 特别处理：如果已经找到了当前方程的解之一，怎么移动都可以，往左或往下或往左下都行。

完整代码如下所示：

• 时间复杂度：$O(n)$ 。
• 空间复杂度：$O(1)$ 。

class Solution {
public:
    vector<vector<int>> findSolution(CustomFunction& customfunction, int z) {
        vector<vector<int>> ans;
        int x = 1, y = 1000; // x向右,f=(x,y)递增,y向下,f(x,y)递减
        while (x <= 1000 && y >= 1) {
            int tz = customfunction.f(x, y);
            if (tz == z) { // x,y合适
                ans.push_back({x, y});
                ++x; // 或者--y
            } else if (tz < z) ++x; // tz太小,增加x以增加tz
            else --y; // tz太大,减少y以减少tz
        }
        return ans;
    }
};