题目

剑指 Offer 33. 二叉搜索树的后序遍历序列【中等】

题解

二叉搜索树性质：左<根，右>根
后序遍历序：左右根

递归分治

利用递归求解，[ i,j ]区间中找到第一个比根节点大的元素，下标为m，则[i,m-1]为左子树 ，[m,j-1]为右子树，下标 j 为根。
指针为p，返回值为 p==j && dfs(i,m-1) && dfs(m,j-1)。

class Solution {
    public boolean verifyPostorder(int[] postorder) {
        int n=postorder.length;
        return dfs(postorder,0,n-1);
    }
    public boolean dfs(int[] postorder,int i,int j){
        if(i>=j)
            return true;
        int p=i;
        //找到第一个比根节点大的元素
        while(postorder[p]<postorder[j])
            p++;
        int m=p;
        while(postorder[p]>postorder[j])
            p++;
        return p==j&&dfs(postorder,i,m-1)&&dfs(postorder,m,j-1);            
    }
}

时间复杂度：$O(n^2)$

空间复杂度：$O(n)$

单调栈

观察下面这棵树，

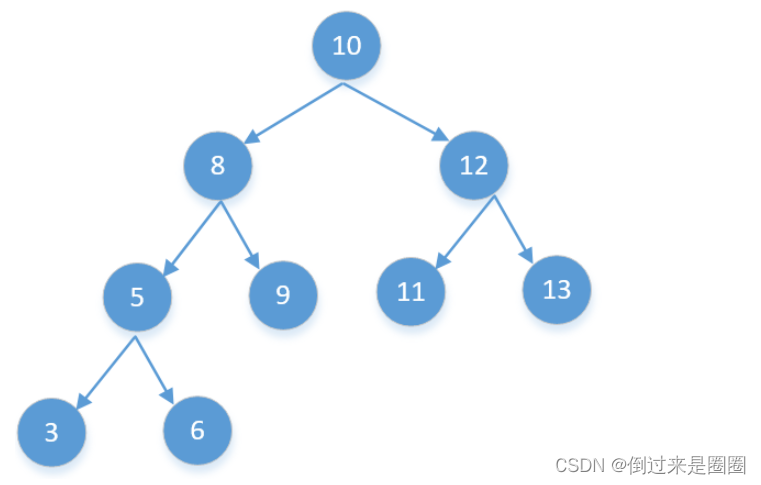
它的后序遍历序：[3,6,5,9,8,11,13,12,10]，如果倒序过来就会变成：[10,12,13,11,8,9,5,6,3]

两个规律：

• 如果arr[i]<arr[i+1]，那么arr[i+1]一定是arr[i]的右子节点
• 如果arr[i]>arr[i+1]，那么arr[i+1]一定是arr[0]……arr[i]中某个节点的左子节点，并且这个值是大于arr[i+1]中最小的（如8号root右子中的最左子11号）

根据以上规律，建升序的单调栈

class Solution {
    public boolean verifyPostorder(int[] postorder) {
        int n=postorder.length,parent=Integer.MAX_VALUE;
        Deque<Integer>stack=new LinkedList<>();
        for(int i=n-1;i>=0;i--){
            int cur=postorder[i];
            //当如果前节点小于栈顶元素，说明栈顶元素和当前值构成了倒序
            //说明当前节点是前面某个节点的左子节点，我们要找到他的父节点
            while(!stack.isEmpty()&&cur<stack.peek()){
                parent=stack.pop();
            }
            if(cur>parent)
                return false;
            stack.push(cur);
        }
        return true;
    }
}

时间复杂度：$O(n)$

空间复杂度：$O(n)$