一、为什么Transformer需要对输入进行位置编码
因为Transformer的输入并没有内涵位置信息,同样的词在不同位置,或者同一个序列以不同顺序输入,对应的词间都会得到相同的注意力权重和输出,但是在NLP领域,词的顺序会极大地影响句子的含义。
句子1:小明喜欢上了小红
句子2:小红喜欢上了小明
对于这两个句子,分词、embedding处理后得到的词向量是相同的,都是“小红”、“小明”、“喜欢”、“上”、“了” 对应的词向量,它们会以下图的方式计算self-attention

图一
在输入Transformer模型时,只是词向量的顺序不同,但是在计算self-attention时(以“小红”为例,用小红的q,分别与其他token的k相乘,计算相关性a,然后在呈上相应的v的到向量)

图二
所以,哪怕是顺序不同,每个token对应的词向量b 依旧不变,这个问题RNN就不需要考虑,因为在RNN模型中,token是一个接一个进入其中的,它们进入的顺序已经隐含了位置信息。
二、Transformer的Positional Encoding是如何进行确定位置信息的呢?
首先说一下Transformer中位置编码是使用正余弦函数进行编码的,公式如下:

看到这个,肯定会有小伙伴提出疑问了,为什么是sin()、cos()函数呢?为什么里面是10000呢?小小脑袋,大大问号❓❓❓ 别急别急,咱们一个一个来。
1、为什么是sin()、cos()函数呢?
正如图二所示,在求self-attention时,先求qi与kj相乘,求贡献力度aj,然后再用贡献力度aj 乘 vj,之后在相加,得出第i个输入对应的encoder输出。(艾玛,太抽象了,建议看图二)

可以看到,q * k展开之后的第二项,可以理解为绝对位置,就是token(i)和token(j)分别对应的位置P(i)、P(j),,,最后一项,既包括pi也包括pj,和两个位置都有关。
这能说明式子展开之后,已经具备了绝对位置信息,还没有具备相对位置信息,但是有一项表达式和两个位置都有关(最后一项),那我们能不能将最后一项通过人为设定P(x)的表达式,让其隐含相对信息呢?(为什么要希望同时具备绝对位置、相对位置?因为这样更能表示两个变量之间的具体位置呀)
答案是肯定的,这就是位置编码的由来,也就是上面那个公式,具体推导如下:

那么如何才能实现简化之后的式子呢??? 主要是这个g(x)函数怎么构造呢,当时的研究人员就绞尽脑汁的想啊想啊,突然灵光一现,想到了正余弦函数:

这样使用正余弦函数,恰好能满足g(x)的需求,能完成我们的设想。这就是正余弦函数的由来。👏👏👏
那对于多维的编码来说呢,由于内积满足叠加性,更高维度的编码可以看成两两一组的结合:

为什么里面是
 呢?
呢?

那么通过一个相似公式,我们就把问题转换为积分的渐进估计问题了,把这积分的图像画出来,观察一下:

随着(m-n)的增大,也就是相对距离的增大,积分结果逐渐下降。
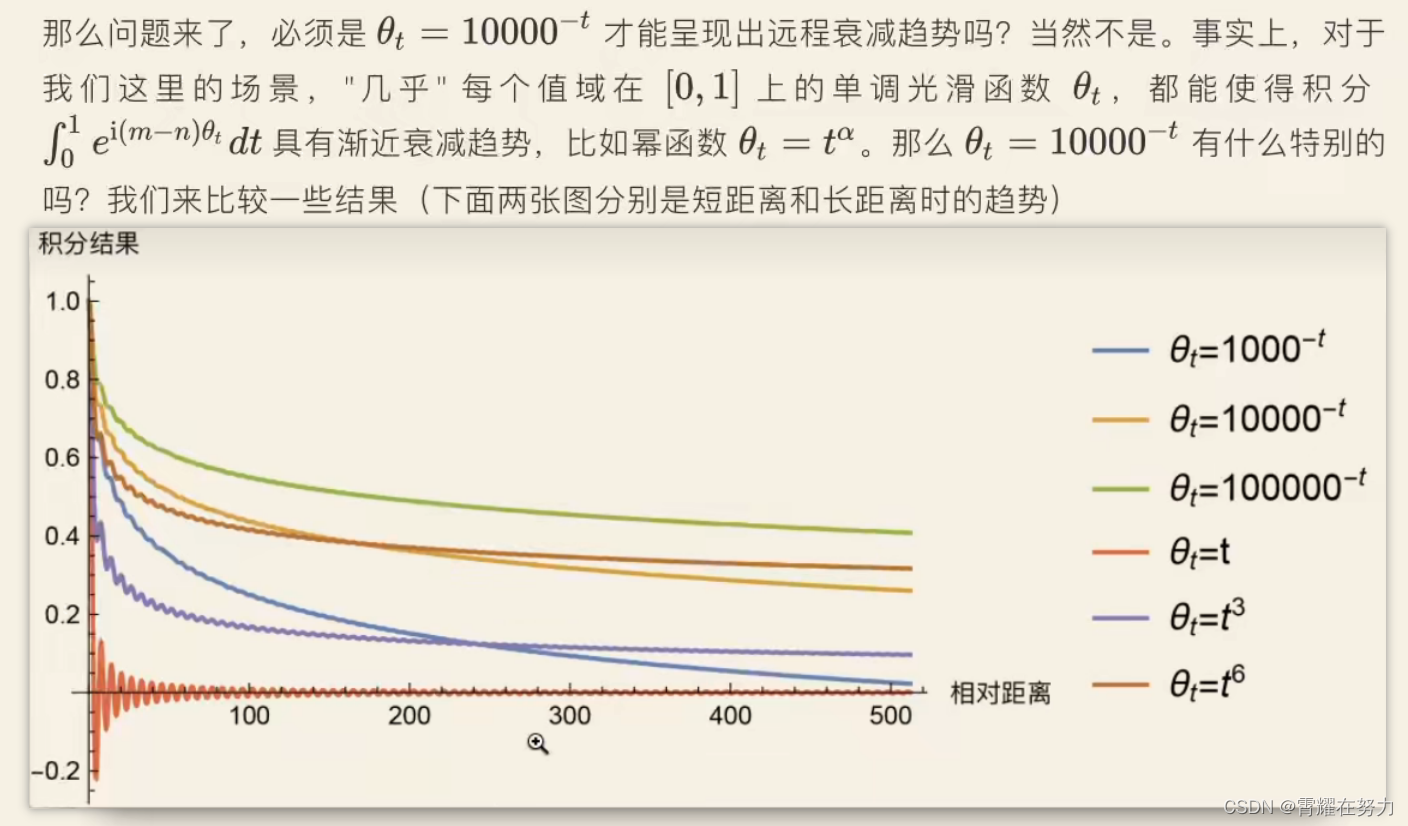
可以看到,这里做了很多实验,验证那个数值比较好一些,但是像10000对应的橙色的曲线一定是最好的吗?好像并不是,,,如果让我们选的话,好像1000对应的 蓝线 更好一些。 随意这个就是研究人员选取的,没必要太过于纠结为什么是10000.