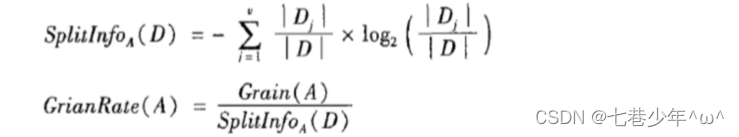第六章.决策树(Decision Tree)
6.1 ID3算法,C4.5算法
1.决策树适用的数据类型
比较适合分析离散数据,如果是连续数据要先转换成离散数据再做分析
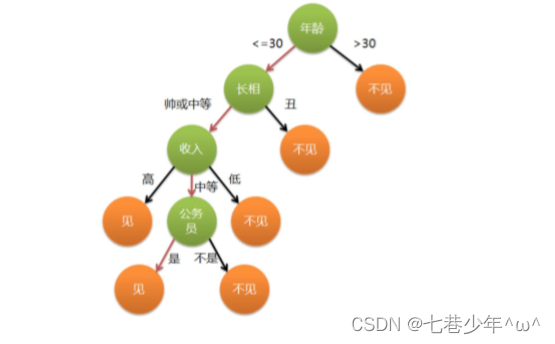
2.信息熵
1).概念:
- 一条信息的信息量大小和它的不确定性有直接的关系,要搞清楚一件非常不确定的事情(或者是我们一无所知的事情),需要了解大量信息->信息量的度量就等于不确定性的多少
2).公式:
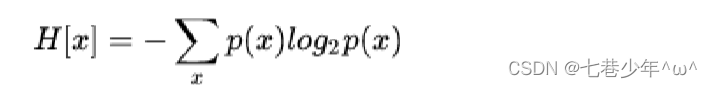
3).示例:
-
示例1:
假设有一个普通骰子A,扔出1-6的概率都是1/6;骰子B,扔出1-5的概率为10%,扔出6的概率为50%,骰子C,扔出6的概率为100% -
计算:
①.骰子A:

②.骰子B:
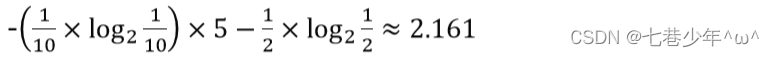
③.骰子C:

3.ID3算法
决策树会选择最大化信息增益来对结点进行划分。
1).信息增益计算公式:
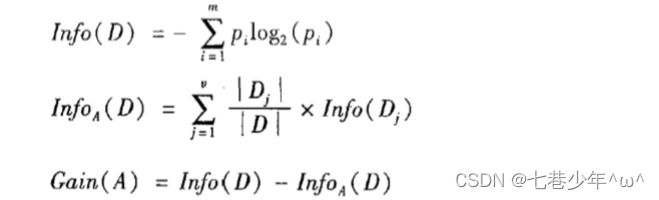
2).公式示例:
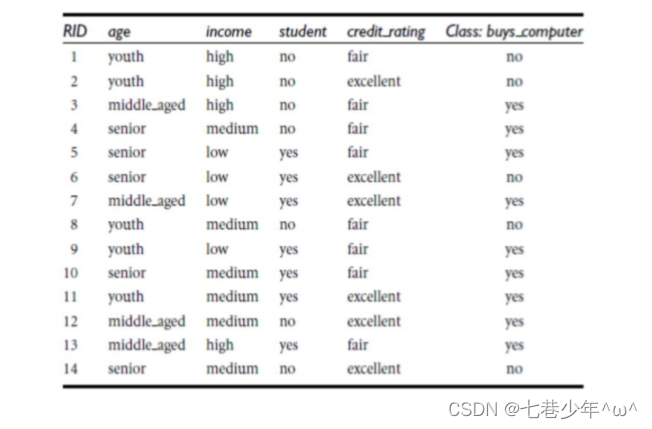
- 分析:
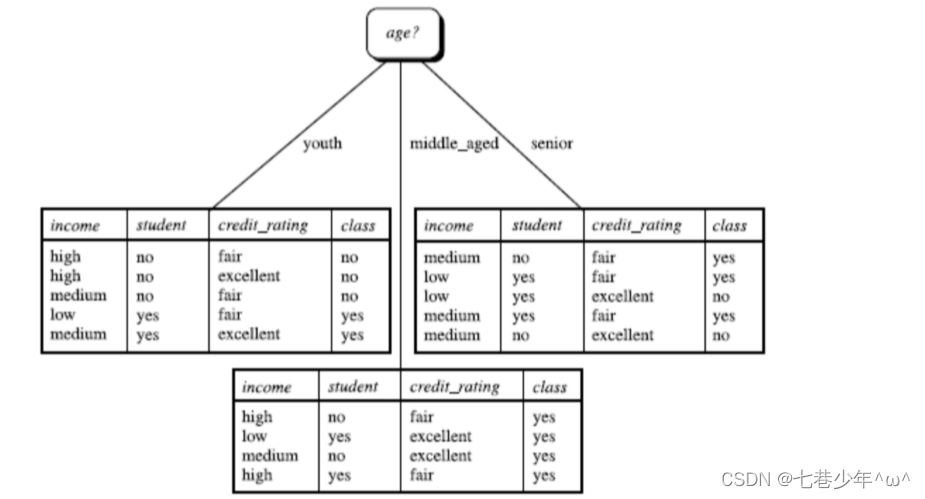
- 计算:

说明:
①.9/14,5/14对应Class:buys_computer那一列。
3).ID3算法示例:
·AllElectronics.csv中的数据:
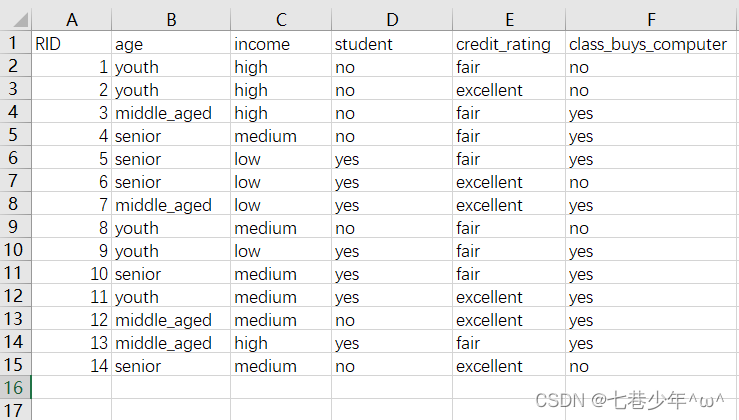
·代码:
from sklearn.feature_extraction import DictVectorizer
from sklearn import tree
from sklearn import preprocessing
import graphviz
import csv
# 导入数据
DTree = open(r'D:\\data\\AllElectronics.csv', 'r')
reader = csv.reader(DTree)#使用import csv是因为表格中含有很多字符
# 获取第一行数据
headers = reader.__next__()
# print(headers)
# 定义两个列表
featureList = []
labelList = []
for row in reader:
# 把Label存入List
labelList.append(row[-1])
rowDict = {}
for i in range(1, len(row) - 1):
# 建立一个数据字典
rowDict[headers[i]] = row[i]
featureList.append(rowDict)
# print(featureList)
# 把数据转换成01表示
vec = DictVectorizer()
x_data = vec.fit_transform(featureList).toarray()
# print('x_data:'+ str(x_data))
# 打印属性名称
feature_names = vec.get_feature_names_out()
# print(feature_names)
# 打印标签
# print('labelList:'+ str(labelList))
# 把标签转换成01表示
lb = preprocessing.LabelBinarizer()
y_data = lb.fit_transform(labelList)
# print('y_data'+str(y_data))
# 创建并拟合模型
DTree_model = tree.DecisionTreeClassifier(criterion='entropy')
DTree_model.fit(x_data, y_data)
# 测试
x_test = x_data[0]
print('x_test:' + str(x_test))
predictions = DTree_model.predict(x_test.reshape(1, -1))#变成二维数据
print('predict:' + str(predictions))
# 导出决策树
dot_data = tree.export_graphviz(DTree_model, out_file=None, feature_names=feature_names, class_names=lb.classes_,
filled=True, rounded=True, special_characters=True)
graph = graphviz.Source(dot_data)
graph.render('computer')
·结果展示: (文件会保存在运行目录下)
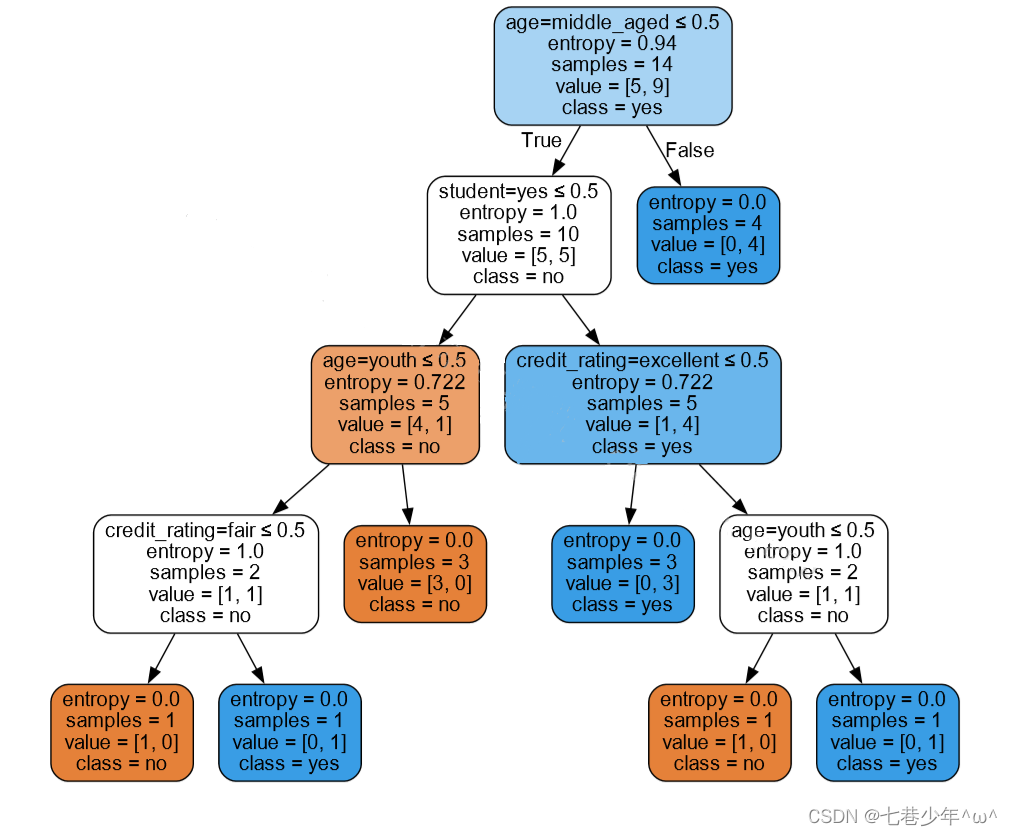
4.C4.5算法
ID3算法存在的缺陷:信息增益的方法倾向于首先选择因子数较多的变量。C4.5算法是ID3算法的优化版本。
1).信息增益的改进-增益率: