数据结构(C++)[B树(B-树)插入与中序遍历,效率分析]、B+树、B*树、B树系列应用
文章目录
- 1. B树
- B树的插入与删除流程
- 2. B+树(MySQL)
- 3. B+树与B树对比
- 4. C++实现B树插入,中序遍历
1. B树
B树类似于二叉排序树,B树可以理解为多叉排序树。
B树和二叉排序树相类似,查找效率取决于树的高度。
因为二搜索树每个节点只能存一个数据。而B树每一个节点可以储存多个值(这些值在这个节点内部按照顺序排序)。
所以一般情况下,B树的高度小于搜索二叉树,效率高。
注意:如果B树的每个节点只保存一个数据,B树就退化为搜索二叉树
- 所以为了避免这种情况,规定除了根节点外,任意m叉树中每一个节点规定至少有[m/2]向上取整,个分叉,至少含有[m/2]-1个数据。
- 多叉树在插入后,高度退化为线性查找,所以规定m叉树任意一个节点的高度相同。
B树的定义:
B树,又称多路平衡查找树,B树中所有结点的孩子个数的最大值称为B树的阶,通常用m表示。一棵m阶B树或为空树,或为满足如下特性的m叉树:
- 树中每个结点至多有m棵子树,即至多含有m-1个关键字。
- 若根结点不是终端结点,则至少有两棵子树(绝对平衡)。
- 除根结点外的所有非叶结点至少有「m/2]棵子树,即至少含有[m/2]-1个关键字。
- 所有的叶结点都出现在同一层次上,并且不带信息(可以视为外部结点或类似于折半查找判定树的查找失败结点,实际上这些结点不存在,指向这些结点的指针为空)
- 每个非叶结点的结构为:(n,A0,K1,A1,K2,A2,… ,Kn,An)其中,Ki(1≤i≤n)为关键字,且Ki<Ki+1(1≤i≤n-1)。Ai(0≤i≤n)为指向子树根结点的指针。且Ai所指子树所有结点中的关键字均小于Ki+1。n为结点中关键字的个数,满足ceil(m/2)-1≤n≤m-1。(关键字按照升序排列,同时保证A0<K1<A1<K2<A2)(多叉搜索树)
需要注意的是计算B树的高度不包括失败节点层
含有n个关键字的m阶B树
最小高度:
每一个节点填满关键字,每一个节点放m-1个关键字
n≤(m-1)(1+m+m^2+...+m^(h-1)),最小高度为logm(n+1)
最大高度:
每一个节点储存最小关键字(分叉数最小),根节点最小有2个分叉,其他节点最小有m/2个分叉
第一层最少有1个节点,第二次有两个,第三次有2(m/2),第四层有2(m/2)*(m/2)...第n层2(m/2)^(h-2)
第n+1层是失败节点,最少有2(m/2)^(h-1)个节点。而n个关键字的B树一定有n+1个叶节点,失败节点
所以n+1≥2(m/2)^(h-1),求解h即可得出最大高度。

B树的插入与删除流程
B树的插入:
连续插入key,在插入key后,若导致原结点关键字数超过上限。则从中间位置_([m/2])将其中的关键字分为两部分。
左部分包含的关键字放在原结点中,右部分包含的关键字放到新结点中,中间位置[m/2]的结点插入原结点的父结点
eg:三阶B树插入关键字(53, 139, 75, 49, 145, 36, 50, 47, 101)
节点最多保存2个关键字,最少保存1个关键字。根节点单独看
- 根节点最多可以保存2个关键字,为了简化插入操作,开辟三个关键字大小,当插入后发现已经满了时再进行分裂。同时多开辟一个空间也有助于在插入时进行排序。
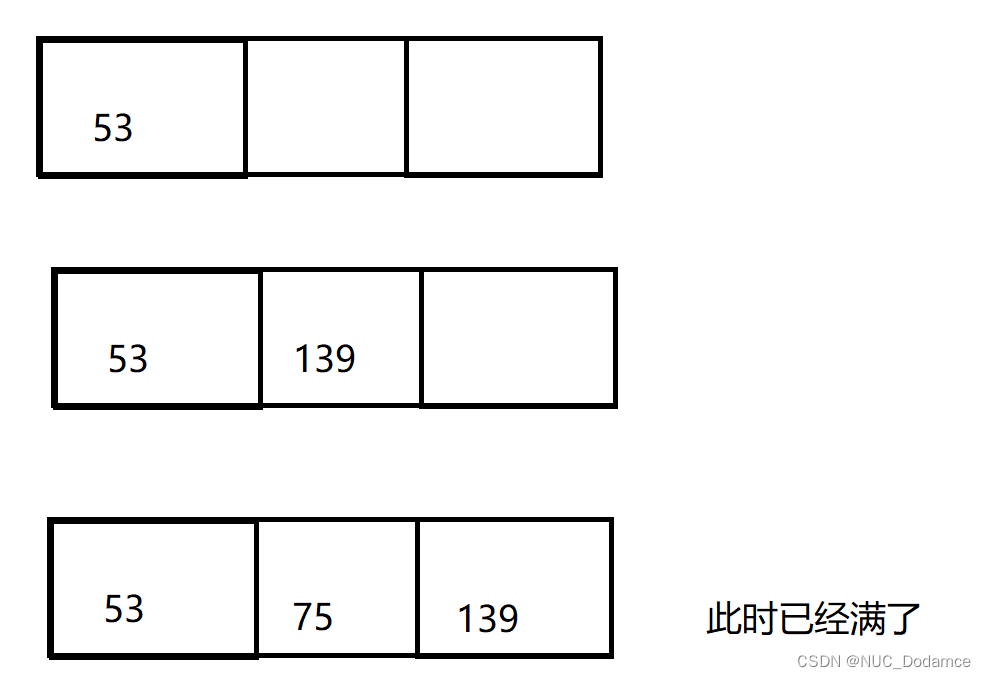
- 如果节点满了,分裂右边一半关键字个数的一般给兄弟节点。提取中位数给父亲,没有父亲就创建新的根节点
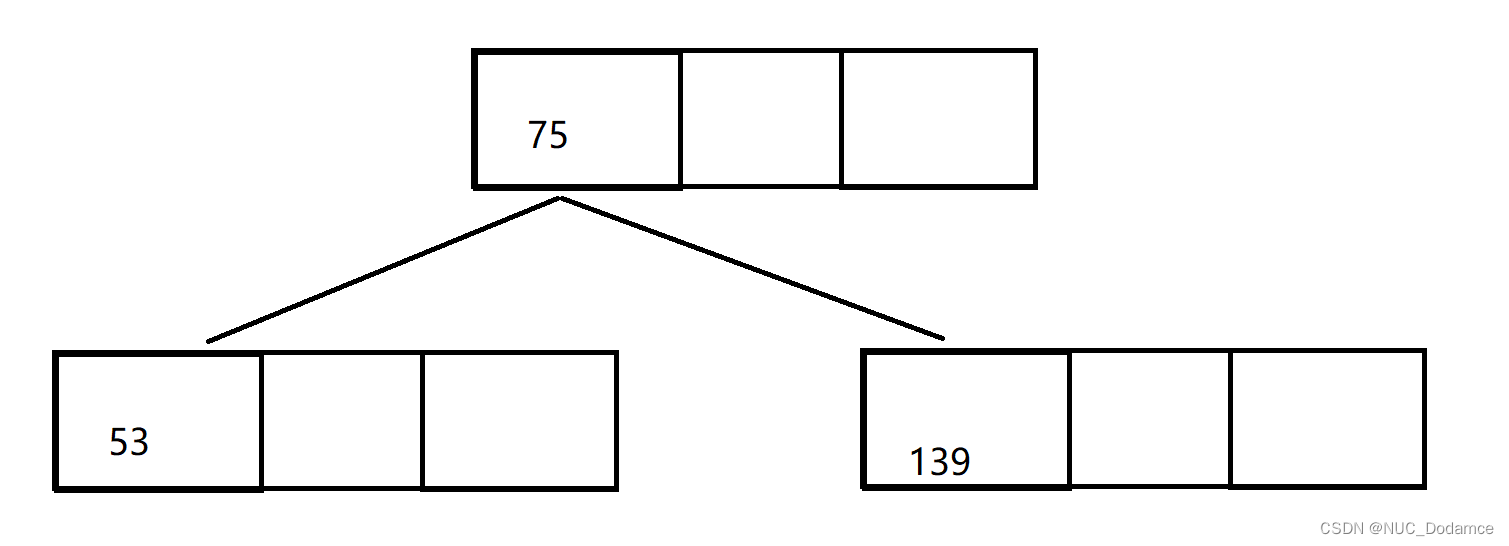
- 继续插入49等后续关键字。
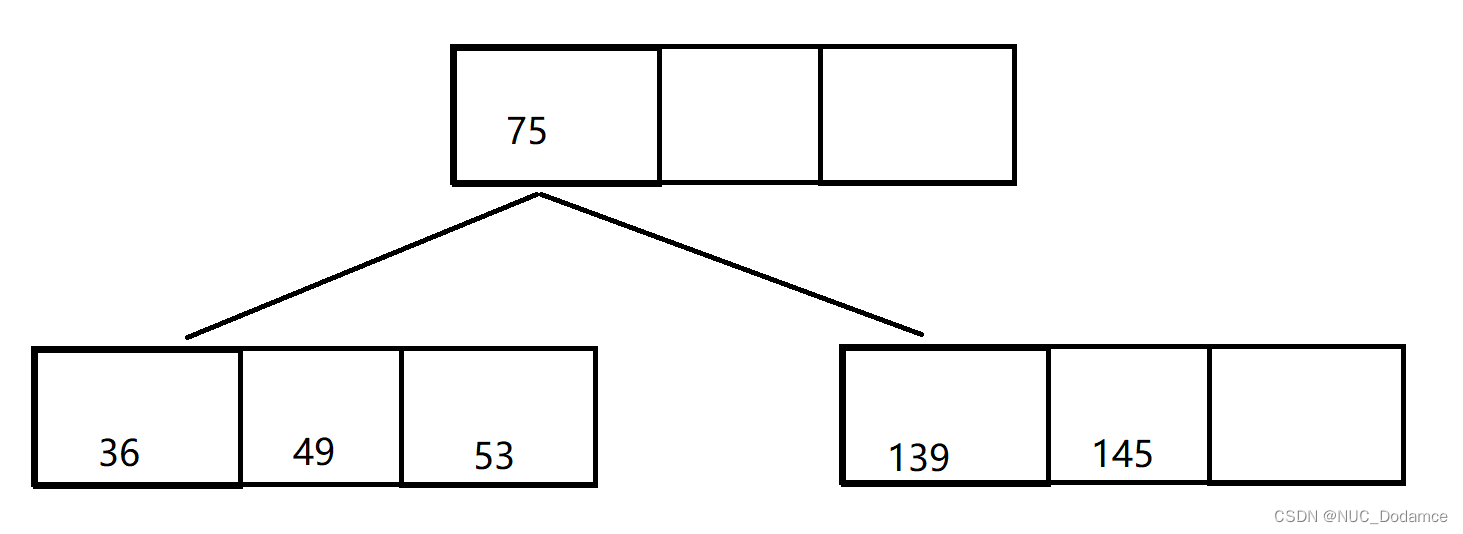
此时节点又满了,需要进行分裂。
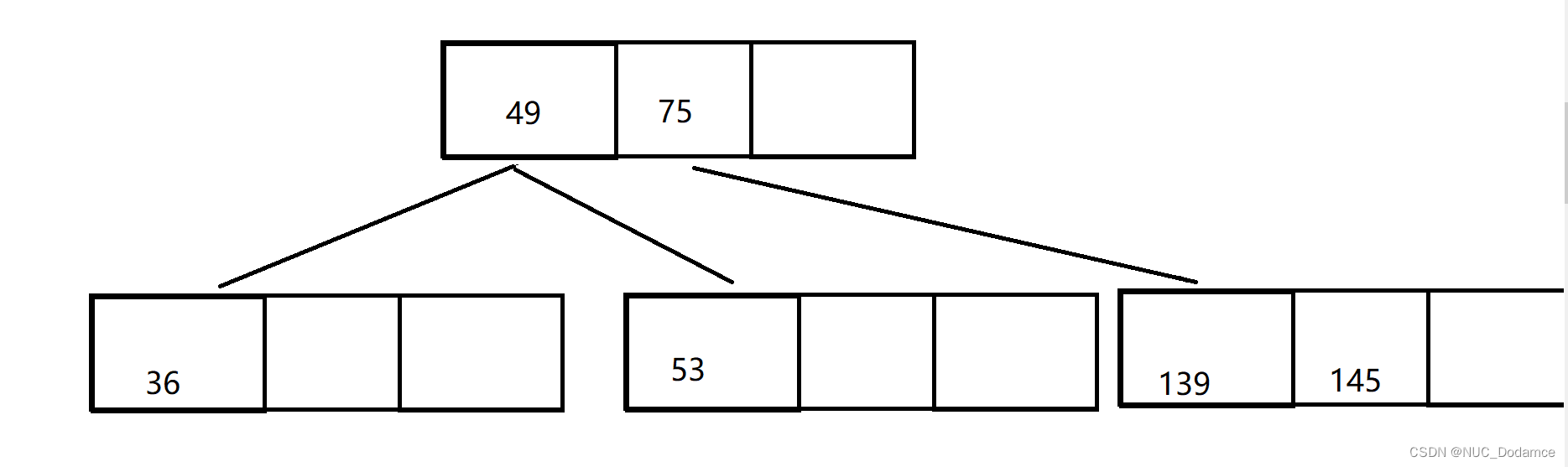
- 继续插入50和47这两个关键字。
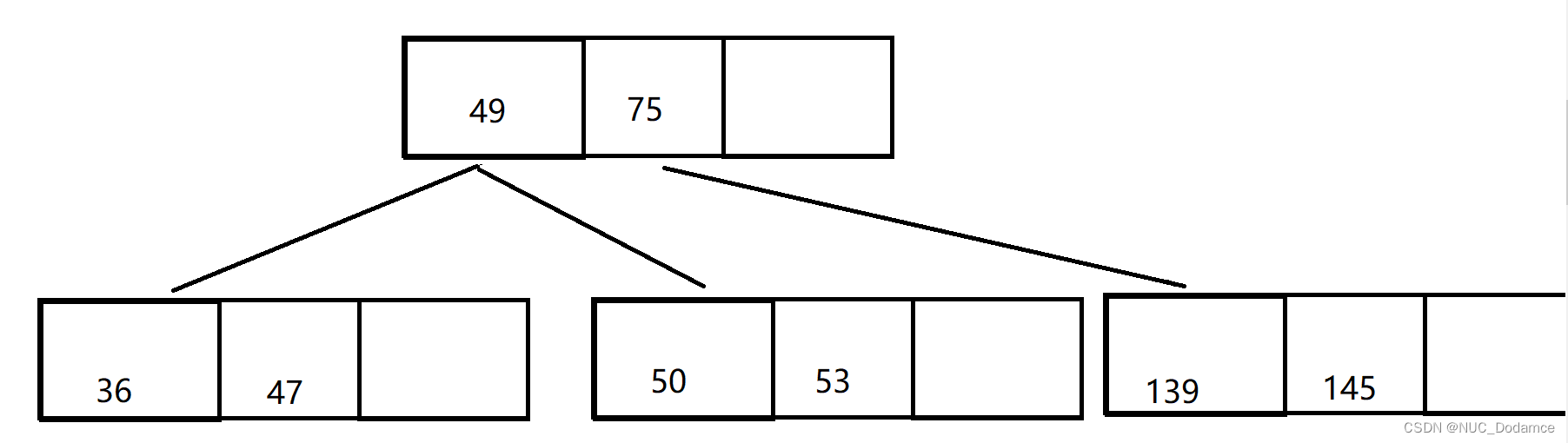
- 最后插入101,导致叶子节点满,需要进行分裂
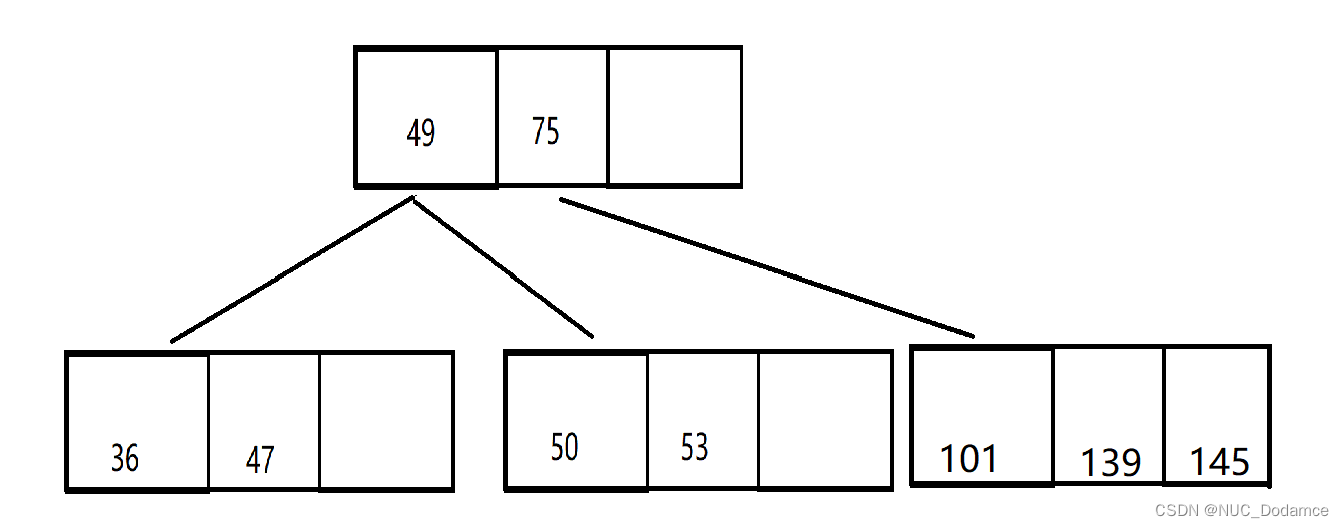
这次分裂会导致两次连续分裂
第一次分裂导致根节点满
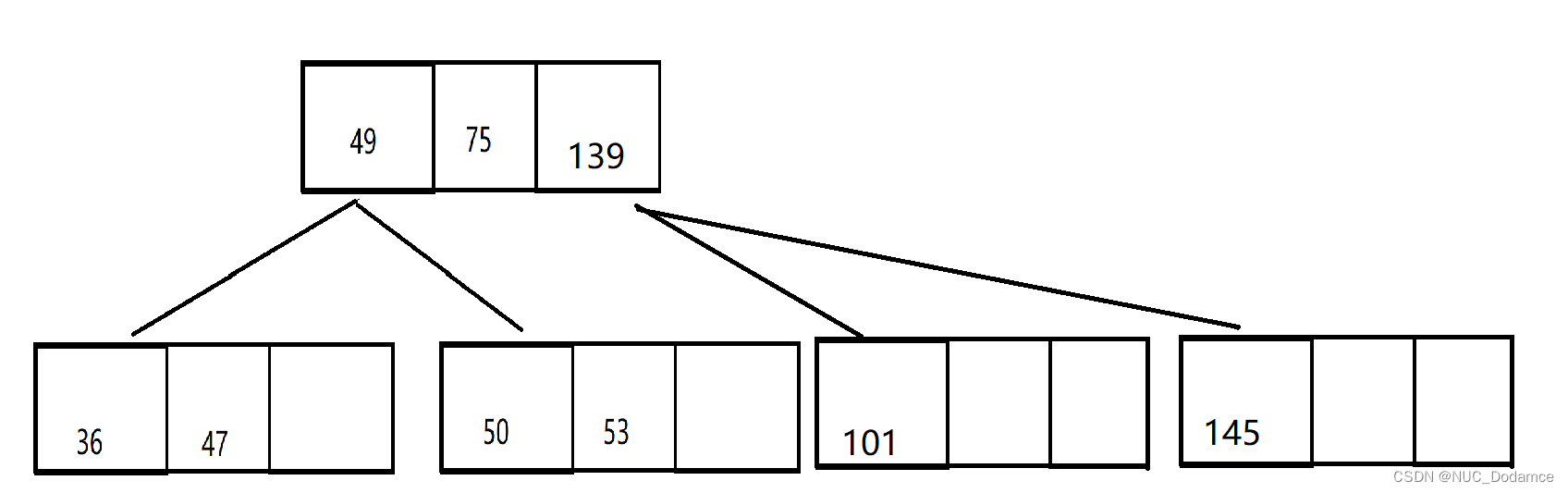
继续分裂根节点,产生新的根节点
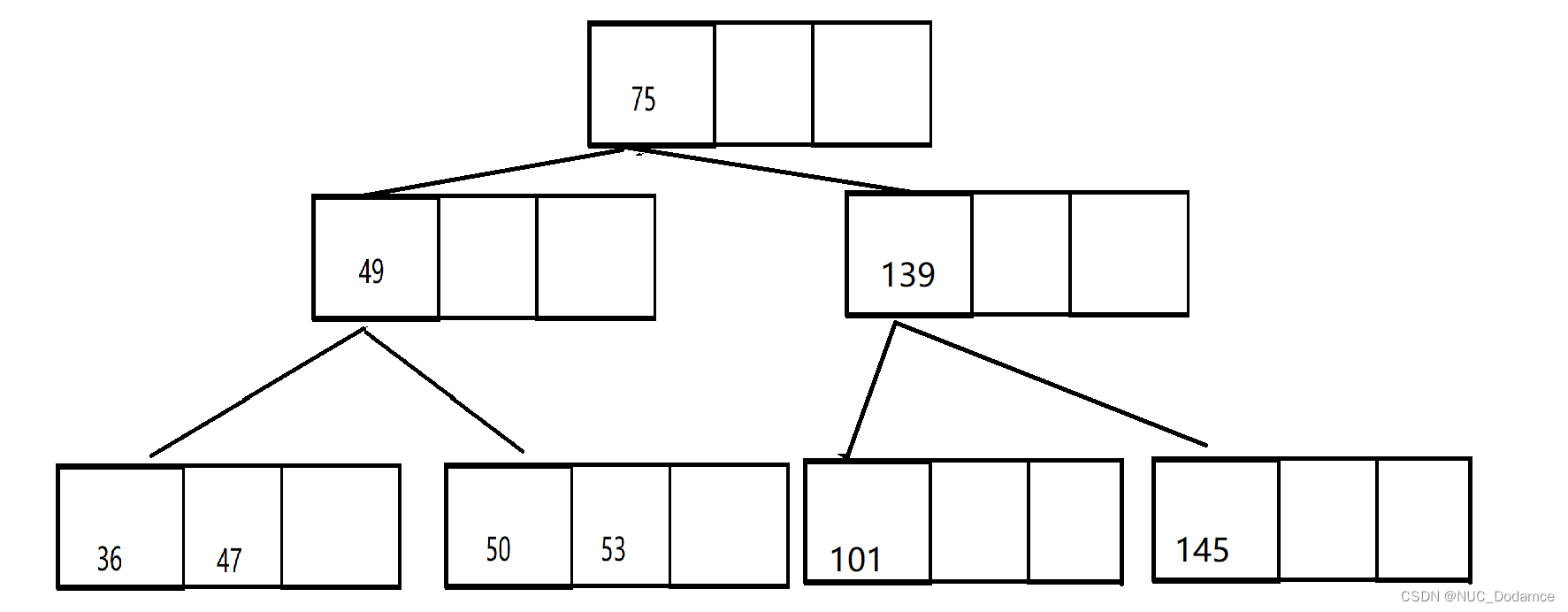
插入完毕
特点
- B树天然平衡,B树是先横向扩展,再竖直生长。所以B树天然平衡
- 新插入的节点一定在叶子插入,叶子节点没有孩子,不影响关键字和孩子的关系
- 叶子节点满了,分裂出一个兄弟,提取中位数,向父亲插入一个值和孩子
- 根节点分裂会增加一层
- 对于B树的每一个节点,这个节点的孩子个数比关键字个数多一个。
B树的删除:
-
若被删除关键字在终端节点,则直接删除该关键字(要注意节点关键字个数是否低于下限[m/2] -1)
-
若被删除关键字在非终端节点,则用直接前驱或直接后继来替代被删除的关键字。这样就转化为对终端节点的删除了。
直接前驱:当前关键字左侧指针所指子树中“最右下”的元素
特别注意:如果删除终端节点到下线,这是需要进行分类处理
-
这个节点的兄弟节点可以借出一个元素时:
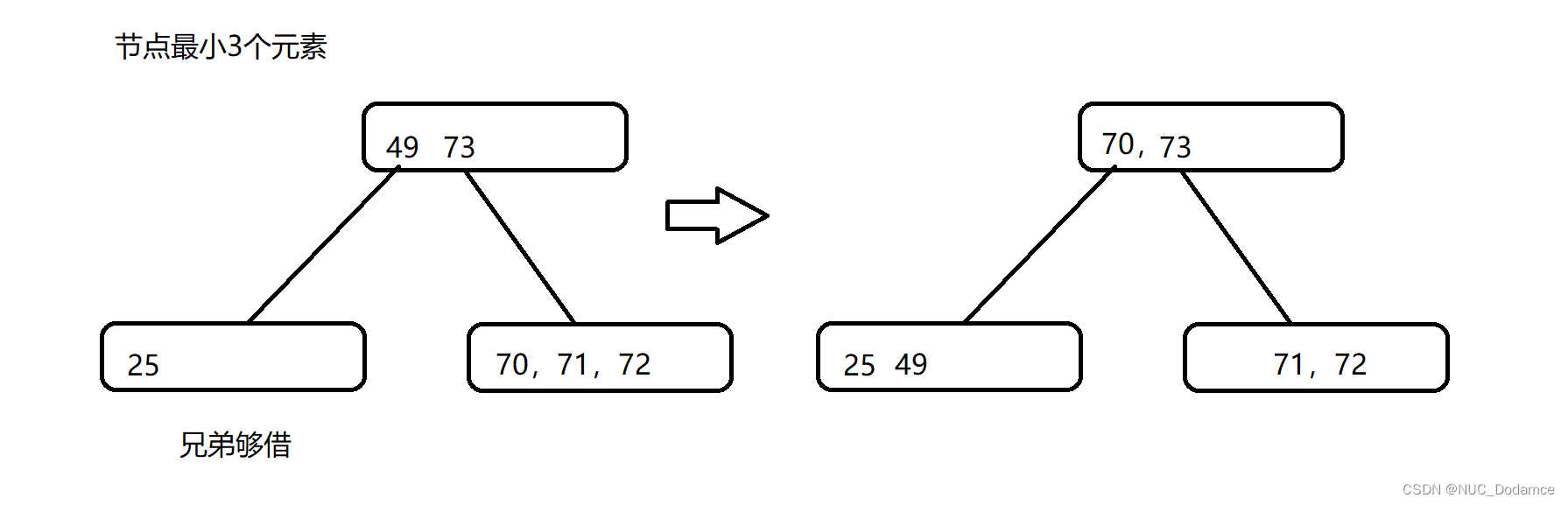

-
兄弟节点不够借用:这个节点和兄弟节点进行合并
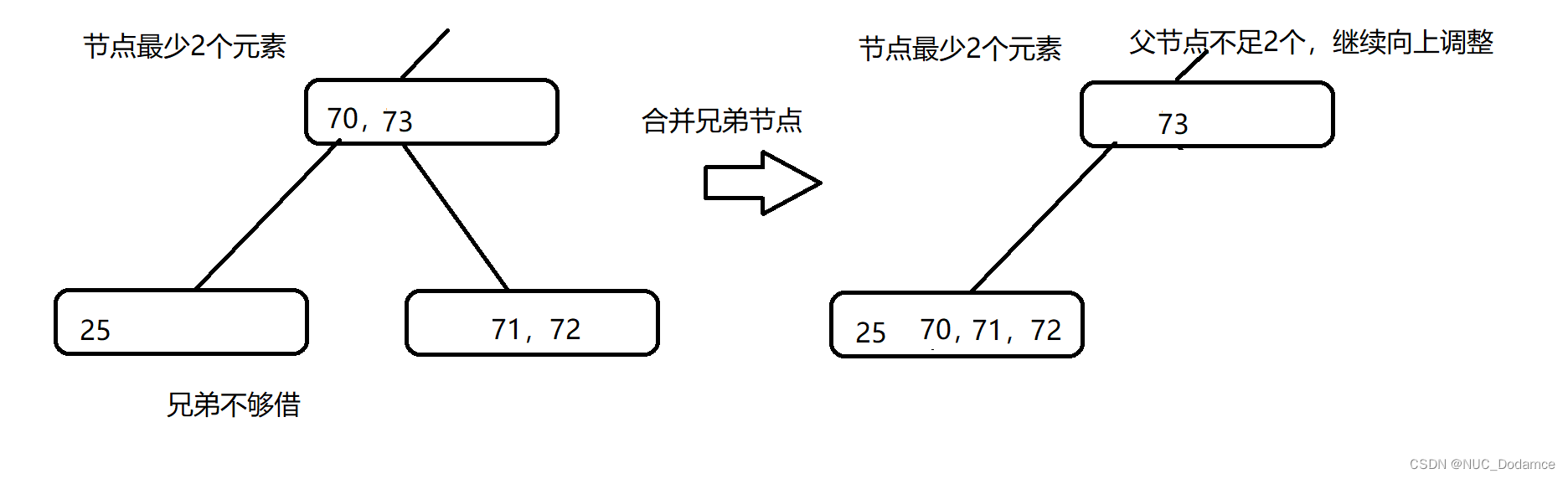
2. B+树(MySQL)
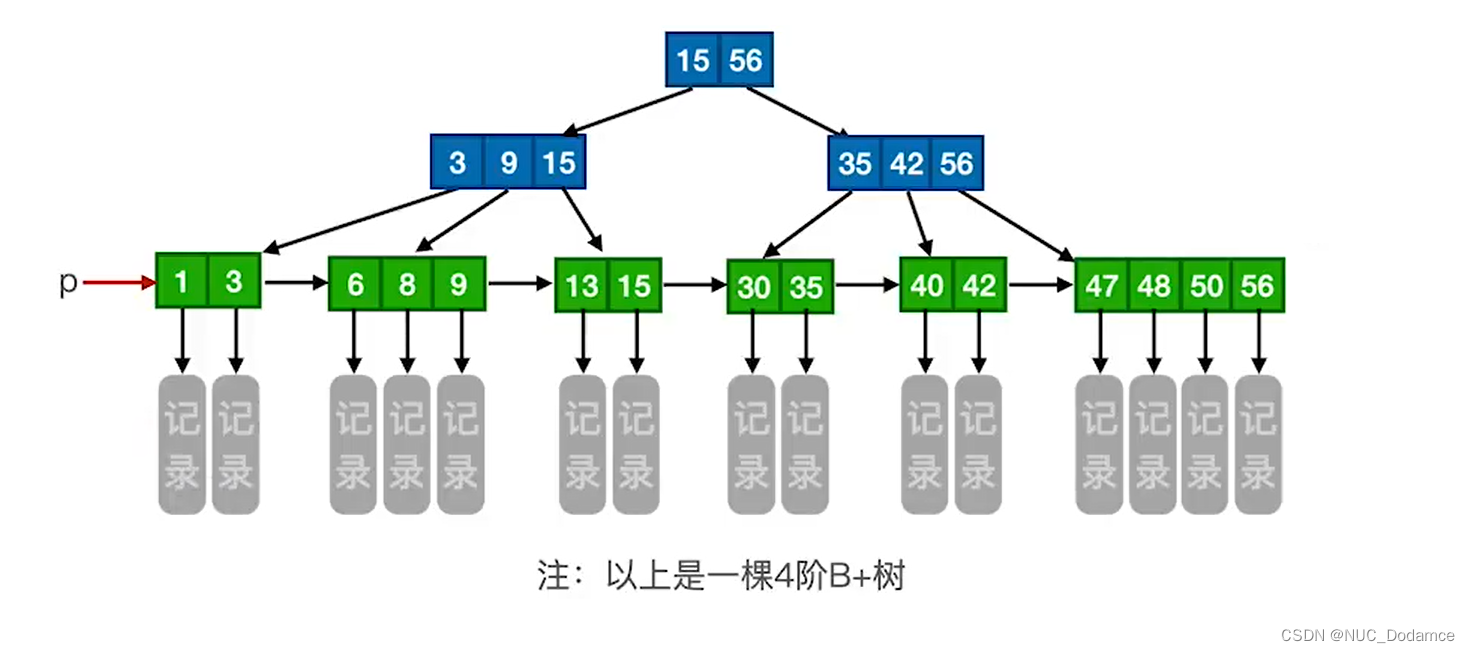
类似于分块查找,一棵m阶的B+树需满足下列条件:
-
每个分支结点最多有m棵子树(孩子结点)。
-
根结点不是叶子节点时至少有两棵子树,其他每个分支结点至少有[m/2]棵子树。
B+树绿色的节点称为叶子节点。蓝色节点(分支节点)又称为"索引"
-
结点的子树个数与关键字个数相等(B树节点两个分支,说明这个节点有三个关键字)
-
所有叶结点包含全部关键字及指向相应记录的指针,叶结点中将关键字按大小顺序排列,并且相邻叶结点按大小顺序相互链接起来。
-
分支节点只包括子节点关键字的最大值和指向子节点的指针。
3. B+树与B树对比
-
m阶B+树节点n个分叉对应n个关键字,m阶B树节点n个分叉对应n-1个关键字
-
m阶B树节点关键字个数范围[(m/2)-1,m-1](根节点[1,m-1])
m阶B+树节点关键字个数范围[m/2,m](根节点[1,m])
-
B+树中,叶节点包含全部关键字,非叶节点出现的关键字也会在叶子节点出现。
B树中,各个节点的关键字不会重复。
-
B+树中,叶结点包含信息,所有非叶结点仅起索引作用,非叶结点中的每个索引项只含有对应子树的最大关键字和指向该子树的指针,不含有该关键字对应记录的存储地址。(查找元素需要一直找到叶节点)
B树的结点中都包含了关键字对应的记录的存储地址(如果中间节点找到了关键字元素,可以直接找到储存地址,无需到叶子节点上)
4. C++实现B树插入,中序遍历
#include <iostream>
#include <vector>
// order阶B树,节点最多order-1个元素,但是需要开辟order大小的空间,因为我是先插入后在判断扩容的
template <class ValueType, size_t order>
struct TreeNode
{
std::vector<ValueType> _value; // 存放节点值
std::vector<TreeNode<ValueType, order> *> _subs; // 存放节点的子树,空间大小为order+1
TreeNode<ValueType, order> *_parent; // 父指针
size_t _size; // 记录实际存储关键字个数
TreeNode()
{
_value.resize(order);
_subs.resize(order + 1);
for (size_t i = 0; i < order; i++)
{
_value[i] = ValueType();
_subs[i] = nullptr;
}
_subs[order] = nullptr;
_parent = nullptr;
_size = 0;
}
};
template <class ValueType, size_t order>
class BTree
{
typedef TreeNode<ValueType, order> TreeNode;
private:
TreeNode *_root = nullptr;
public:
BTree(const std::vector<ValueType> &vet)
{
for (auto &val : vet)
{
insert(val);
}
}
BTree() = default;
bool insert(const ValueType &value)
{
if (_root == nullptr)
{
_root = new TreeNode;
_root->_value[0] = value;
_root->_size += 1;
return true;
}
else
{
// 找要插入的位置
std::pair<TreeNode *, int> ret = _findPos(value);
if (ret.second >= 0)
{
// 不允许冗余
return false;
}
TreeNode *cur = ret.first; // 要插入的节点
int insert_value = value;
TreeNode *child = nullptr;
while (true)
{
_insert(cur, insert_value, child);
if (cur->_size == order)
{
// 节点放满了需要分裂
int mid = order / 2;
TreeNode *node = new TreeNode; // node存放[mid+1,order-1]的数据
size_t pos = 0;
for (size_t i = mid + 1; i < order; i++)
{
node->_value[pos] = cur->_value[i];
node->_subs[pos] = cur->_subs[i];
// 更新父节点
if (cur->_subs[i] != nullptr)
{
cur->_subs[i]->_parent = node;
}
pos += 1;
// 将cur移出的位置清空
cur->_value[i] = ValueType();
cur->_subs[i] = nullptr;
}
// node节点中,新插入的值的孩子节点指针没处理
node->_subs[order] = cur->_subs[order];
if (cur->_subs[order] != nullptr)
{
// 更新父节点
cur->_subs[order]->_parent = node;
}
cur->_subs[order] = nullptr;
node->_size = pos;
cur->_size -= pos + 1; // cur还提取了一个值作为这两个节点父亲,下面的代码会操作
ValueType midValue = cur->_value[mid];
cur->_value[mid] = ValueType();
if (cur->_parent == nullptr)
{
// 新创建父节点,这个节点是cur和node的父亲
_root = new TreeNode;
_root->_value[0] = midValue;
_root->_subs[0] = cur;
_root->_subs[1] = node;
_root->_size = 1;
cur->_parent = _root;
node->_parent = _root;
break;
}
// 转划为向cur->_parent这个位置插入midValue问题,可以通过while循环解决
insert_value = midValue;
child = node;
cur = cur->_parent;
}
else
{
// 节点没有插满,插入结束
return true;
}
}
}
return true;
}
// 删除指定元素
void erase(const ValueType &value)
{
std::pair<TreeNode *, int> ret = _findPos(value);
if (ret.second == -1)
{
// 没有找到删除的元素
return;
}
else
{
TreeNode *del = ret.first;
if (!_isLeave(del))
{
// 如果删除的节点不是终端节点,转化为终端节点后在删除
TreeNode *prev = del->_subs[ret.second]; // 找直接前继节点(左子树的最右节点)
while (prev->_subs[ret.second + 1] != nullptr)
{
prev = prev->_subs[ret.second + 1];
}
// 交换节点,转化为删除终端节点
ValueType delValue = del->_value[ret.second];
del->_value[ret.second] = prev->_value[prev->_size - 1];
prev->_value[prev->_size - 1] = delValue;
erase(delValue);
}
else
{
// 是终端节点,找其兄弟节点
/**
* @brief 考研对B树的代码不怎么考核,而删除的代码比较复杂,需要找这要删除这个节点的兄弟节点
* 出于时间考虑,这里先空开。
* 我认为删除节点操作需要找到删除节点的B树节点指针才行,这样才能准确的找到删除节点的兄弟B树节点的位置
*/
}
}
}
void disPlayInorder()
{
_disPlay(_root);
}
private:
bool _isLeave(TreeNode *node)
{
bool ret = true;
for (int i = 0; i < node->_size; i++)
{
if (node->_subs[i] != nullptr)
{
ret = false;
break;
}
}
return ret && node->_subs[node->_size] == nullptr;
}
void _disPlay(TreeNode *node)
{
if (node == nullptr)
return;
for (size_t i = 0; i < node->_size; i++)
{
_disPlay(node->_subs[i]);
std::cout << node->_value[i] << " ";
}
// 最后剩余右子树
_disPlay(node->_subs[node->_size]);
}
void _insert(TreeNode *node, int value, TreeNode *child)
{
// 在数组中找value插入的位置,需要移动数组
int endPos = node->_size - 1;
while (endPos >= 0)
{
if (value < node->_value[endPos])
{
// 挪动数据
node->_value[endPos + 1] = node->_value[endPos];
node->_subs[endPos + 2] = node->_subs[endPos + 1];
endPos -= 1;
}
else
{
break;
}
}
// endPos位置是第一个值小于value的位置,value要插入到其后边
node->_value[endPos + 1] = value;
node->_subs[endPos + 2] = child;
if (child != nullptr)
{
child->_parent = node;
}
node->_size += 1;
}
// 查找要插入的叶子节点以及数组下标
std::pair<TreeNode *, int> _findPos(const ValueType &value)
{
TreeNode *par = nullptr;
TreeNode *cur = _root;
while (cur != nullptr)
{
int pos = 0; // 先从数组下标为0处开始
while (pos < cur->_size)
{
if (value < cur->_value[pos])
{
//_value[pos]左子树
break;
}
else if (value > cur->_value[pos])
{
pos += 1;
}
else
{
return std::make_pair(cur, pos);
}
}
par = cur;
cur = cur->_subs[pos];
}
return std::make_pair(par, -1);
}
};
#include "BTree.h"
using namespace std;
int main(int argc, char const *argv[])
{
vector<int> ret = {2, 4, 1, 5, 7, 6, 0, 9, 3, 8};
BTree<int, 5> tree(ret); // 5阶B树
tree.disPlayInorder();
// tree.erase(6);
return 0;
}
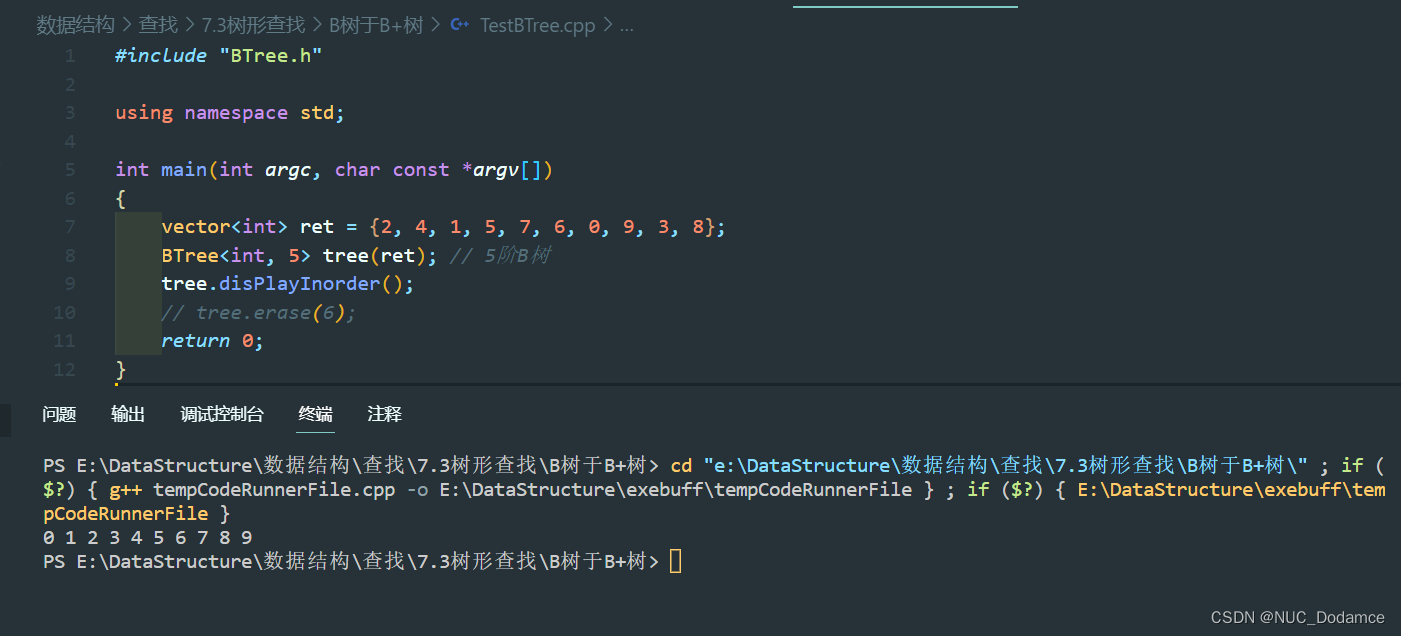
代码仓库