🍎 博客主页：🌙@披星戴月的贾维斯
🍎 欢迎关注：👍点赞🍃收藏🔥留言
🍇系列专栏：🌙 蓝桥杯
🌙我与杀戮之中绽放，亦如黎明的花朵🌙
🍉一起加油，去追寻、去成为更好的自己！
蓝桥杯倒计时 39天

提示：以下是本篇文章正文内容，下面案例可供参考

---

🍎、递推

🍉、递推的简单定义

递推算法是一种用若干步可重复运算来描述复杂问题的方法。递推是序列计算中的一种常用算法。通常是通过计算前面的一些项来得出序列中的指定项的值。

🍉、递推问题分析的四个步骤

1、确定递推变量
2、建立递推关系
3、确定初始（边界）条件
4、对递推过程进行控制

🍉、递推改变一个位置的通用模板函数

void turn(char &c)
{
    if(c == 'W') c = 'B'; //这个状态需要根据每一题题目具体分析
    else c = 'W';
}

对递归结果和测试用例的看法：有时候我们的答案和样例会不一样，这是很正常的，我们只要输出一个正确的答案就ok了。

---

🍎、例题分析

🍇、（AcWing）砖块

本题链接: 砖块

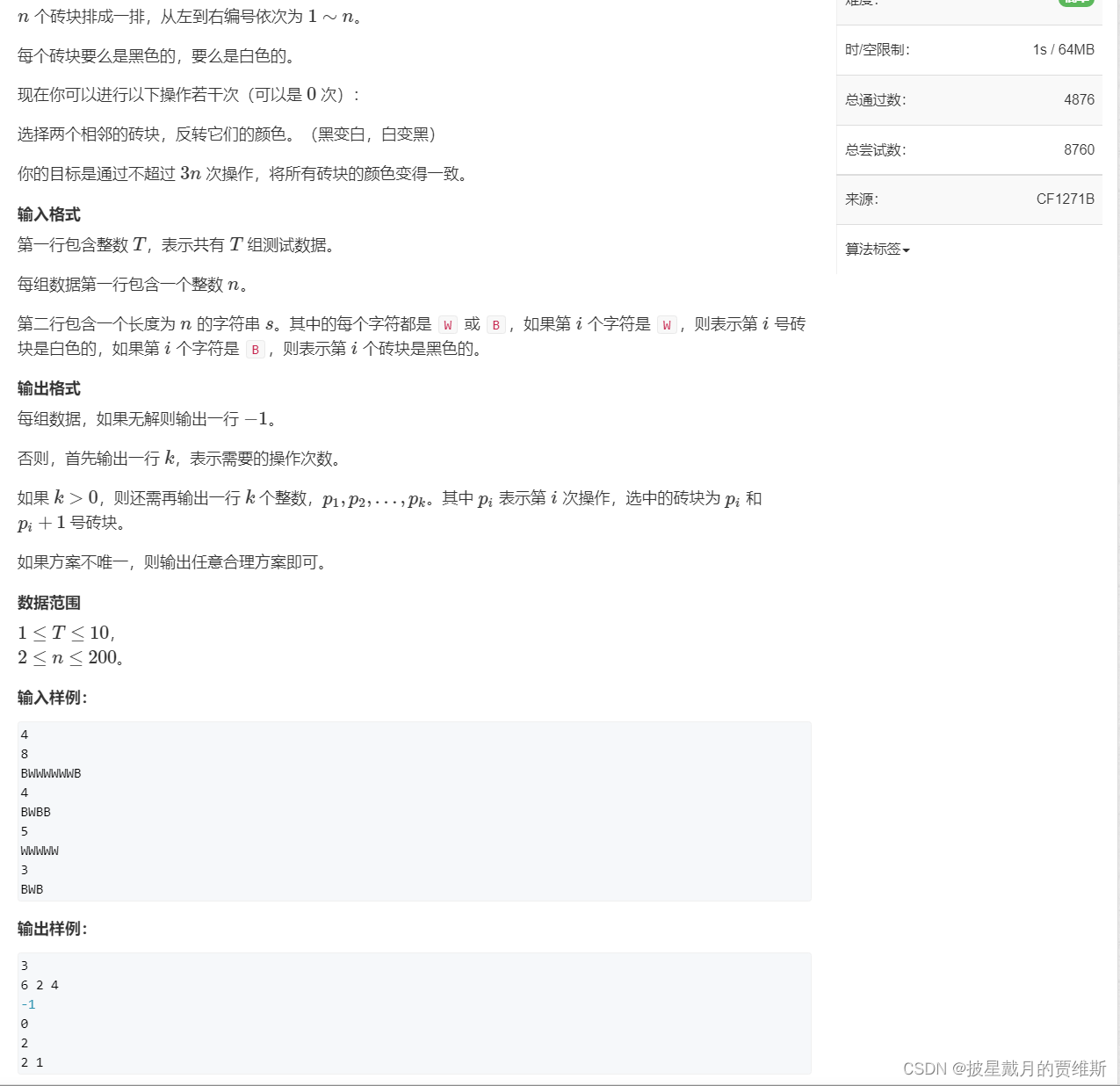
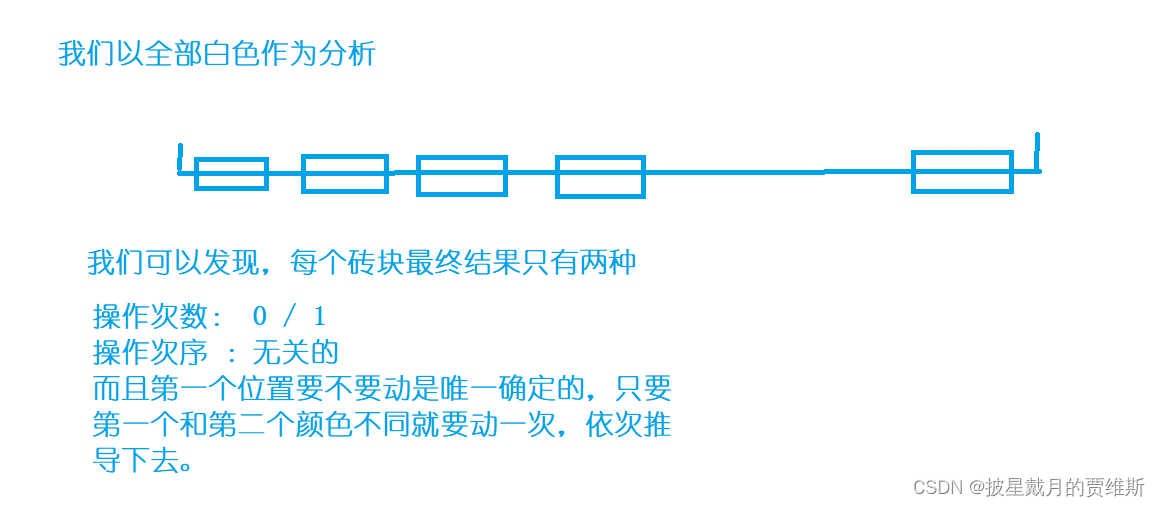
代码示例：

#include<iostream>
#include<algorithm>
#include<string>
#include<vector>
using namespace std;
const int N  = 203;
int t, n;
string str;
void update(char &c)
{
    if(c == 'W') c = 'B';
    else c = 'W';
}
bool cheak(char c)
{
    vector<int> res; // 存所有的方案
    string s = str; //设置s字符串拷贝原str
    for(int i = 0; i + 1 < n; i++)
    {
        if(s[i] != c)
        {
            update(s[i]);
            update(s[i + 1]);
            res.push_back(i);//说明那个位置要被操作一下，要把这个方案记录到res里
        }
    }
    if(s.back() != c) return false;
    
    cout << res.size() << endl;
    for(int x : res) cout << x + 1 << " ";
    if(res.size()) cout << endl; // 如果方案数为0，直接输出一个回车
    return true;
}
int main ()
{
    
    cin >> t;
    while(t --)
    {
        cin >> n >> str;
        if(!cheak('W') && !cheak('B')) puts("-1");
    }
    
    return 0;
}

🍇、（AcWing）翻硬币

本题链接: 翻硬币

分析解题思路：

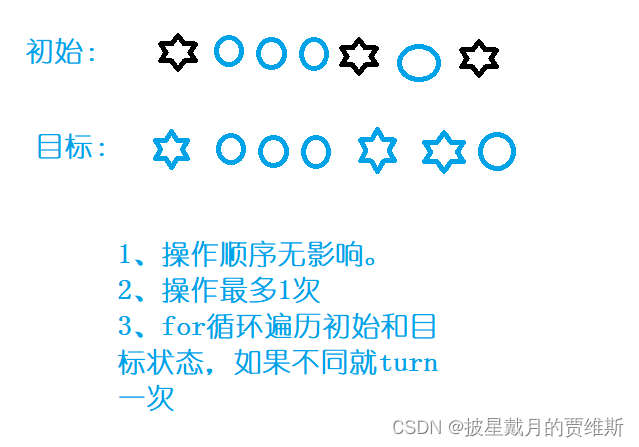
代码示例：

#include<iostream>
#include<algorithm>
#include<string>
using namespace std;

string a, b;
void turn(char &c)
{
    if(c == 'o') c = '*';
    else c = 'o';
}
int main ()
{
    cin >> a >> b;
    int res = 0;
    for(int i = 0; i + 1<  a.size(); i++ )
    {
        if(a[i] != b[i])
        {
            turn(a[i]);
            turn(a[i + 1]);
            res++;
        }
    }
    cout << res << endl;
    
    return 0;
}

🍇、（AcWing）费解的开关

本题链接: 费解的开关

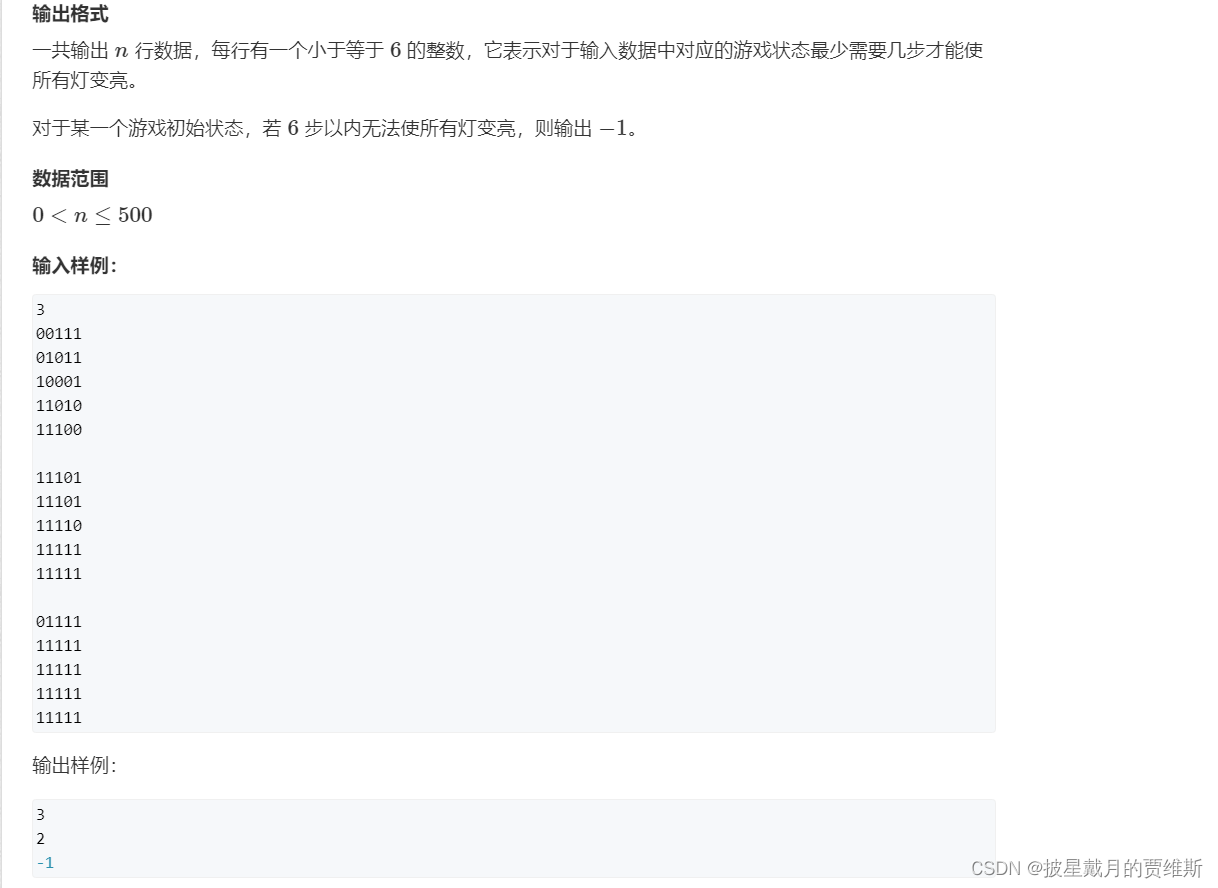
解题分析：
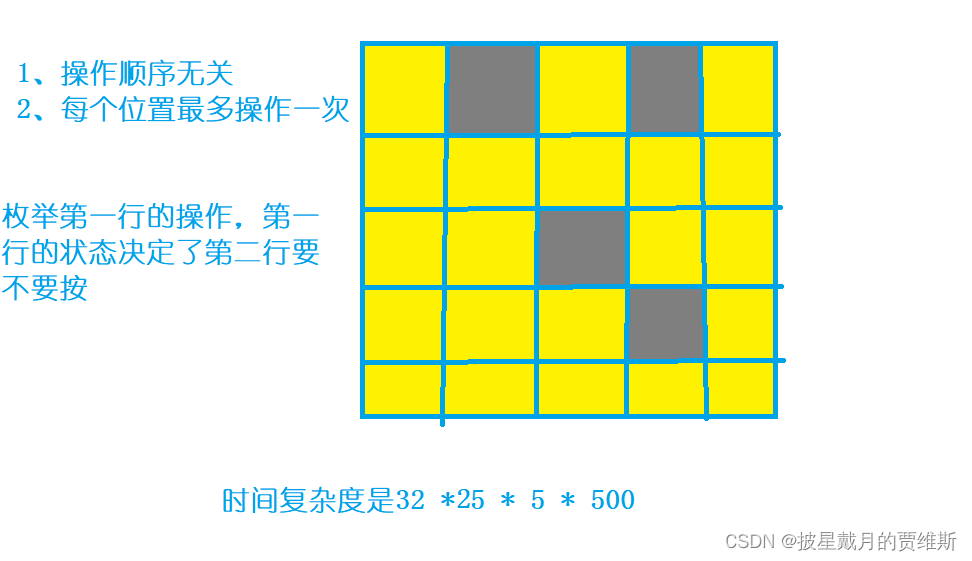代码示例：

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;

const int INF = 1000000;
const int N = 6;
char g[N][N], backcup[N][N];
int dx[5] = { 0, -1, 0, 1, 0}, dy[5] = { 0, 0, 1, 0, -1};
void turn(int x, int y)
{
    for(int i = 0; i < 5; i++)
    {
        int a = dx[i] + x, b = dy[i] + y;
        if(a >= 0 && a < 5 && b >= 0 && b < 5)
        {
            g[a][b] ^= 1;
        }
    }
}
int work()
{
    int ans = INF;
    for(int k = 0 ; k < 32; k++) //k从0枚举到32，是枚举每个位置对应的状态，是不是turn过
    {
        int res = 0; // 当前方案操作数的最小值
        char backcup[N][N];
        memcpy(backcup, g, sizeof g);
        for(int j = 0; j < 5; j++)//针对第一层的操作
            if(k >> j & 1) //位运算
            {
                res ++;
                turn(0, j);
            }
            
        for(int i = 0; i < 4; i++)
            for(int j = 0; j < 5; j++)
            if(g[i][j] == '0')
            {
                res++;
                turn(i + 1, j);
            }
        bool is_successful = true;
        for(int j = 0; j < 5; j++)
            if(g[4][j] == '0')
            {
                is_successful = false;
                break;
            }
        if(is_successful) ans = min(ans, res);    
        memcpy(g, backcup, sizeof g);
    }
    if(ans > 6) ans = -1;
    return ans;
    
}


int main ()
{
    int T;
    cin >> T;
    while(T--)
    {
        for(int i = 0; i < 5; i++) cin >> g[i];
        cout << work() << endl;
    }
    
    return 0;
}

---

🍎、总结

    本文简要介绍了递推算法的简要概念和几道递推算法的经典例题，希望大家读后能有所收获！