递归算法的两个特点（很重要）

调用自身

要有结束条件

void func1(int x)
{
    printf("%d\n", x);
    func1(x - 1);
}

func1会一直死循环，没有使其结束的条件，所以不是递归

void func2(int x)
{
    if (x > 0)
    {
        printf("%d\n", x);
        func2(x + 1);
    }
}

func2当传入的x > 0时，会一直死循环，此时没有使其结束的条件，所以不是递归

void func3(int x)
{
    if (x > 0)
    {
        printf("%d\n", x);
        func3(x - 1);
    }
}

func3是递归，满足递归的两个特点，调用自身，有结束条件

输出结果为：3 2 1

void func4(int x)
{
    if (x > 0)
    {
        func4(x - 1);
        printf("%d\n", x);
    }
}

func4是递归，满足递归的两个特点，调用自身，有结束条件

输出结果为：1 2 3

递归实例:汉诺塔问题

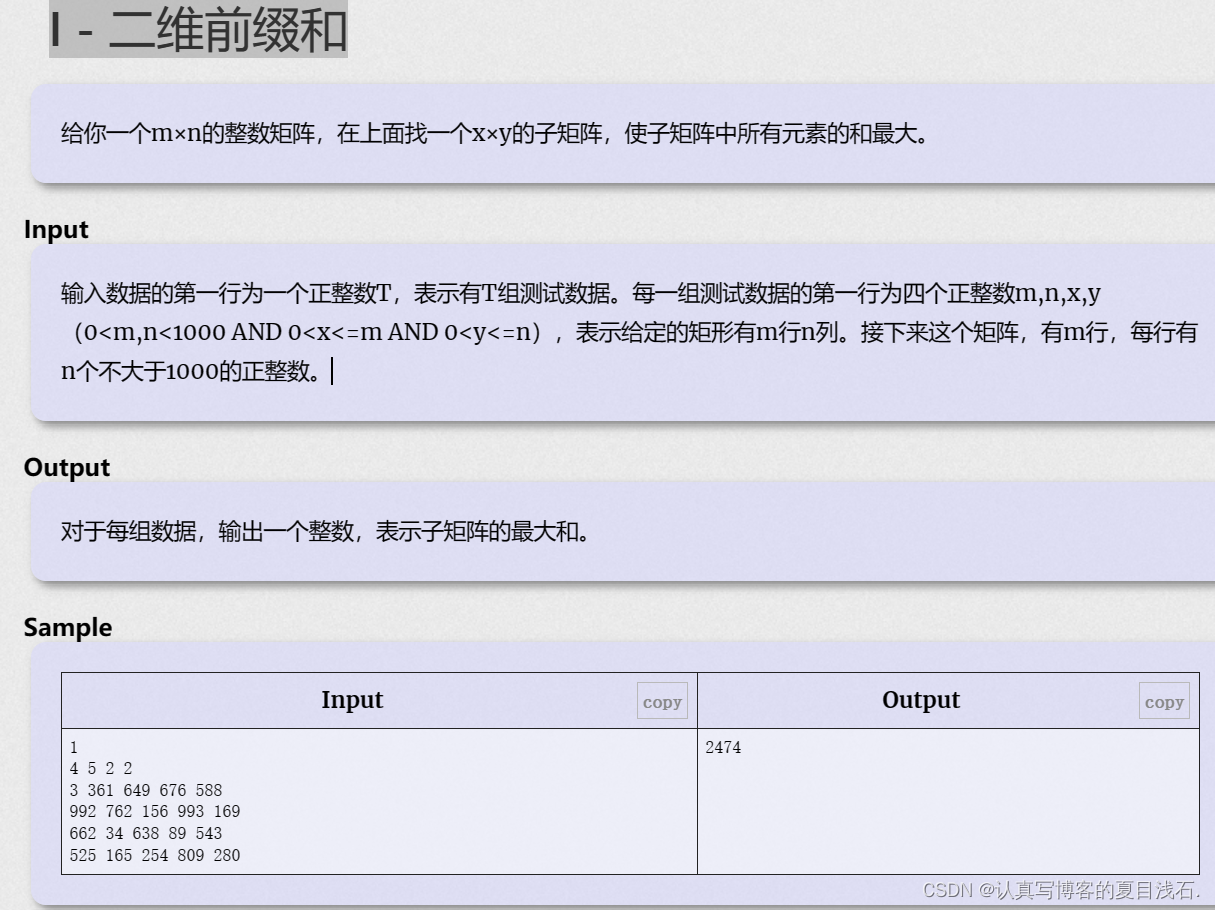
汉诺塔（Tower of Hanoi），又称河内塔，是一个源于印度古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。

分析：

当A柱子只有1个盘子时

A移动到B

当A柱子有2个盘子时

A移动到C

A移动到B

C移动到A

当A柱子有n个盘子时，将A柱子中的第n个盘子看作一个整体，A柱子中的1, 2, ..., n-1看作一个整体

hanoi(n - 1)从A移动到C

A移动到B

hanoi(n - 1)从C移动到B

源码：

#include <stdio.h>

long long g_counter = 0;
void move(int n, char a, char b)
{
    g_counter++;
    printf("第%d次移动，将第%d个盘子从%c移动到%c\n", g_counter, n, a, b);
}
void hanoi(int n, char a, char b, char c)
{    
    if (n == 1)
    {
        move(n, a, b);
    }
    else
    {
        hanoi(n-1, a, b, c);
        move(n, a, b);
        hanoi(n-1, c, a, b);
    }
}

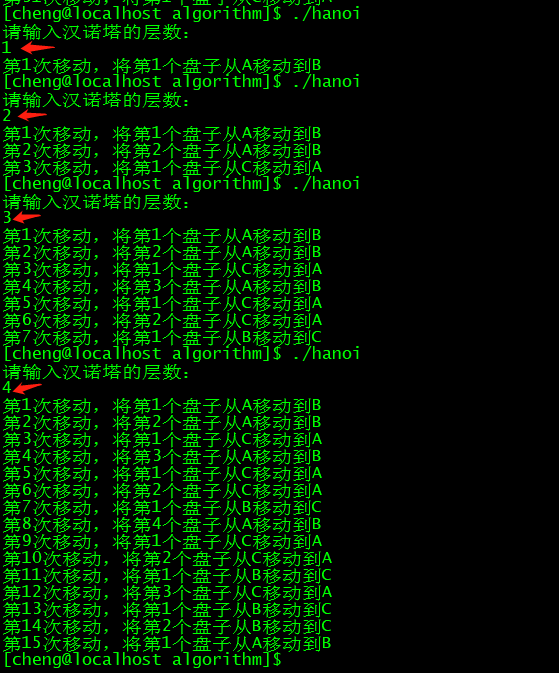
int main(int argc, char *argv[])
{
    int n = 3;
    printf("请输入汉诺塔的层数：\n");
    scanf("%d", &n);
    hanoi(n, 'A', 'B', 'C');

    return 0;
}

结果