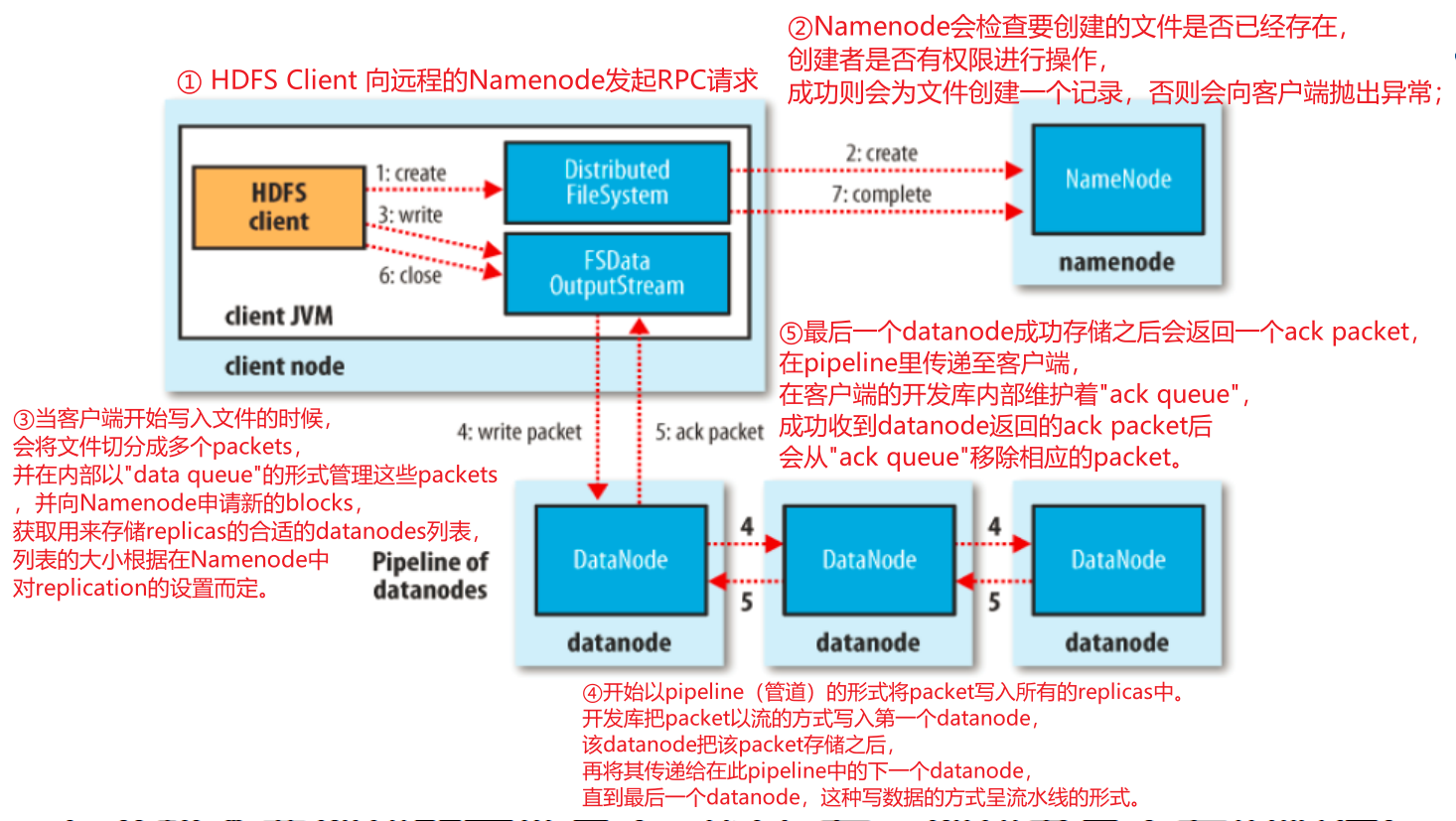
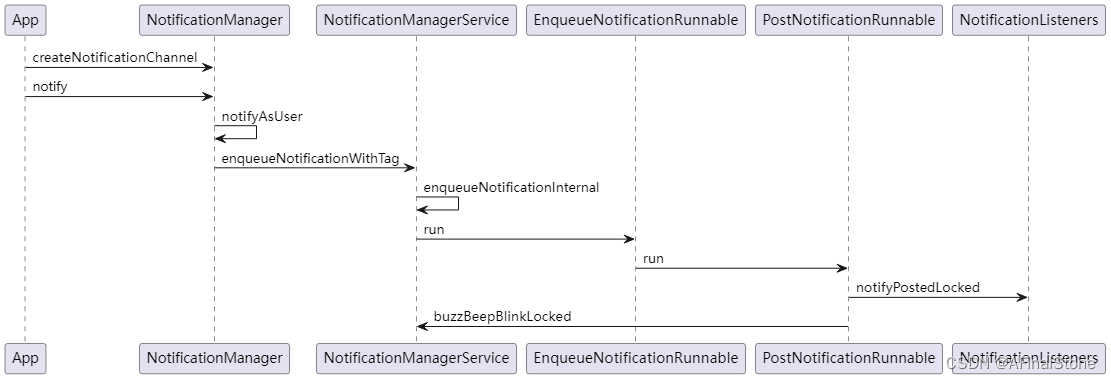
原教程地址:KalmanFilter.NET
卡尔曼滤波广泛应用在雷达系统(目标跟踪)中,但是其实它还可以应用在任何需要估算和预测的领域。
一、一维卡尔曼滤波
通过8个数值例子介绍卡尔曼滤波,涉及平均数、方差、标准差等,最终可以自行设计出一个一维的卡尔曼滤波算法。
1.1 背景知识
平均值、期望值、方差、标准差
对于一个跟踪和控制系统,最大的问题计时在存在不确定性的前提下提供一个准确的有用信息。
卡尔曼滤波就是一种常用且重要的估算方法,它在预估时默认输入信息不准确,同时也根据上一次系统的预估值来预估下一次的系统状态,测量噪声和处理噪声的存在可能使得动态模型(描述输入与输出关系的方法)估算出来的结果与真实值相差甚远,因此需要对噪声进行处理。
平均值和期望值的区别在于,用可观测状态计算出的是均值,一般用 μ \mu μ 表示,而对于无法获得真实值的隐变量,平均多次测量值估计的结果称为期望值,一般用 E E E 表示。
方差和标准差,方差 Variance 用来衡量一组结果的离散程度,标准差 Standard Deviation 则是方差的算数平方根,两者分别用
σ
2
\sigma^2
σ2 和
σ
\sigma
σ 表示。
方差、标准差在完全样本中的计算和在抽样样本中的计算是有区别的
在完全样本中:
σ
2
=
1
N
∑
n
=
1
N
(
x
n
−
μ
)
2
,
σ
=
1
N
∑
n
=
1
N
(
x
n
−
μ
)
2
\sigma^2=\frac{1}{N}\sum^{N}_{n=1}(x_n-\mu)^2,\sigma=\sqrt{\frac{1}{N}\sum^{N}_{n=1}(x_n-\mu)^2}
σ2=N1n=1∑N(xn−μ)2,σ=N1n=1∑N(xn−μ)2
在抽样样本中:
σ
2
=
1
N
−
1
∑
n
=
1
N
(
x
n
−
μ
)
2
,
σ
=
1
N
−
1
∑
n
=
1
N
(
x
n
−
μ
)
2
\sigma^2=\frac{1}{N-1}\sum^{N}_{n=1}(x_n-\mu)^2,\sigma=\sqrt{\frac{1}{N-1}\sum^{N}_{n=1}(x_n-\mu)^2}
σ2=N−11n=1∑N(xn−μ)2,σ=N−11n=1∑N(xn−μ)2
正太分布
很多自然现象都遵循正太分布,也称为高斯分布,可以通过以下等式描述:
f
(
x
;
μ
,
σ
2
)
=
1
2
π
σ
2
e
−
(
x
−
μ
)
2
2
σ
2
f(x;\mu,\sigma^2)=\frac{1}{\sqrt{2\pi\sigma^2}}e^{\frac{-(x-\mu)^2}{2\sigma^2}}
f(x;μ,σ2)=2πσ21e2σ2−(x−μ)2
高斯曲线也被称为正太分布的概率密度函数,如下图所示,以及正太分布在
μ
±
σ
\mu\pm\sigma
μ±σ、
μ
±
2
σ
\mu\pm2\sigma
μ±2σ、
μ
±
3
σ
\mu\pm3\sigma
μ±3σ 的比例,通常,测量误差呈正太分布。


随机变量分为连续随机变量和离散随机变量,所有的测量值都是连续随机变量。
估计的准确度与精密度
估计用来估算系统的不可见状态,可以通过雷达等传感器估计飞机位置,并通过使用多个传感器和高级估计及追踪算法(如卡尔曼滤波)来显著提升估计精度。
准确度表示测量结果与真实值的接近程度。精密度表示测量结果的再现性。

随机误差导致方差,高/低精密度系统表示系统方差/不确定性的大小,而高/低精度系统表示系统系统性误差(偏差)的大小。对测量值进行平均或平滑处理可以显著降低方差影响,但是无法修复固定的系统误差,教程中案例都假设为无偏系统。
以一张图进行总结

1.2 α − β − γ \alpha-\beta-\gamma α−β−γ 滤波器
静态模型案例-金条称重
估计一个静态模型的状态,
x
^
n
,
n
=
1
n
(
z
1
+
z
2
+
.
.
.
+
z
n
−
1
+
z
n
)
=
1
n
∑
i
=
1
n
(
z
i
)
\hat{x}_{n,n}=\frac{1}{n}(z_1+z_2+...+z_{n-1}+z_n)=\frac{1}{n}\sum^{n}_{i=1}(z_i)
x^n,n=n1(z1+z2+...+zn−1+zn)=n1i=1∑n(zi)
符号说明:
x x x 是测量值
z n z_n zn 是第 n n n 次的测量值
x ^ n , n \hat{x}_{n,n} x^n,n 是第 n n n 次测量后的估计值
x ^ n , n − 1 \hat{x}_{n,n-1} x^n,n−1 是 n − 1 n-1 n−1 次测量后对 n n n 时刻作出的先验估计值
x ^ n + 1 , n \hat{x}_{n+1,n} x^n+1,n 是 n n n 次测量后对 n + 1 n+1 n+1 时刻作出的先验估计值
因为案例中的动态模型是定值,因此 x ^ n + 1 , n = x ^ n , n \hat{x}_{n+1,n}=\hat{x}_{n,n} x^n+1,n=x^n,n
经过计算可以得到
x
^
n
,
n
=
x
^
n
−
1
,
n
−
1
+
1
n
(
z
n
−
x
^
n
−
1
,
n
−
1
)
\hat{x}_{n,n}=\hat{x}_{n-1,n-1}+\frac{1}{n}(z_n-\hat{x}_{n-1,n-1})
x^n,n=x^n−1,n−1+n1(zn−x^n−1,n−1),这就是一个状态更新方程,可以将其总结为:
当前状态估计
=
当前状态估计的先验估计值
+
F
a
c
t
o
r
×
(
测量值
−
当前状态估计的先验估计值
)
当前状态估计=当前状态估计的先验估计值+Factor\times(测量值-当前状态估计的先验估计值)
当前状态估计=当前状态估计的先验估计值+Factor×(测量值−当前状态估计的先验估计值)
这里的
F
a
c
t
o
r
Factor
Factor在卡尔曼滤波中被称为卡尔曼增益,记为
K
n
K_n
Kn ,这里暂以
α
n
\alpha_n
αn 代替
K
n
K_n
Kn,状态更性方程可以写为如下,其中的
(
z
n
−
x
n
,
n
−
1
)
(z_n-x_{n,n-1})
(zn−xn,n−1)为观测残差/更新,包含了新的观测信息。
x
^
n
,
n
=
x
^
n
,
n
−
1
+
α
n
(
z
n
−
x
^
n
,
n
−
1
)
\hat{x}_{n,n}=\hat{x}_{n,n-1}+\alpha_n(z_n-\hat{x}_{n,n-1})
x^n,n=x^n,n−1+αn(zn−x^n,n−1)
下面是整个估计过程:
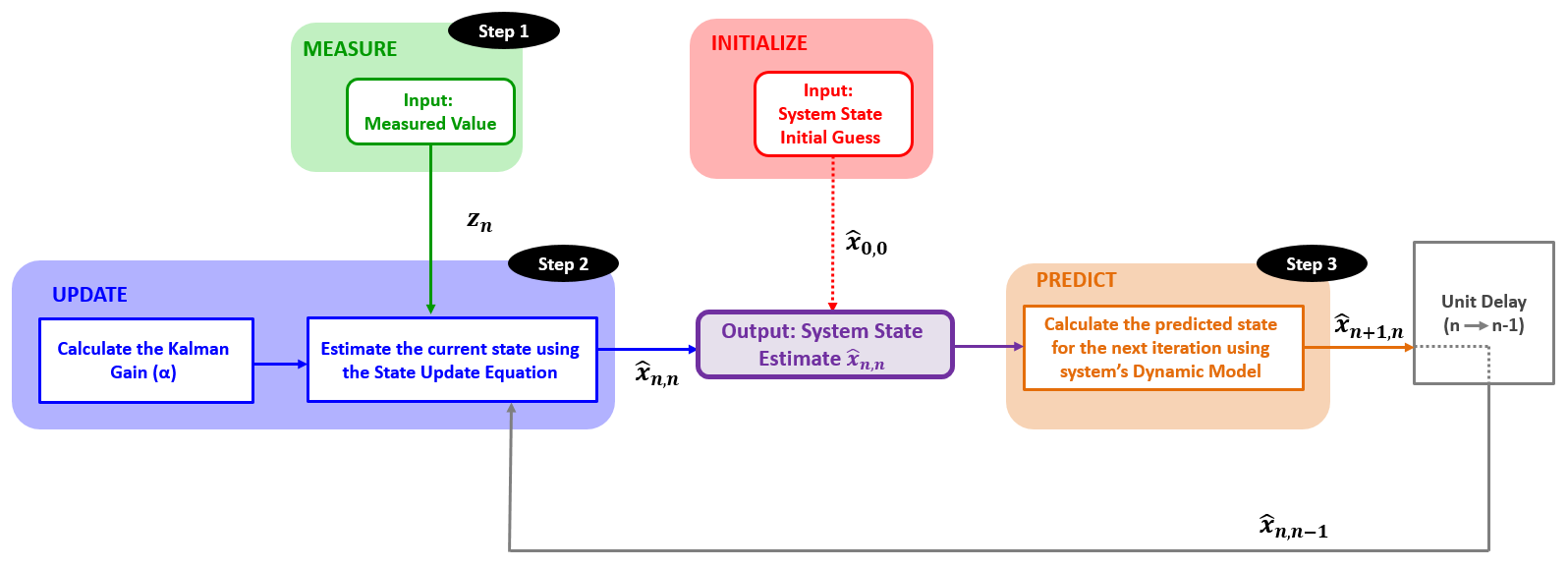
一维空间追踪匀速飞行器
假设一个一维空间,一架飞行器向远离/接近雷达方向恒速飞行,雷达角度、飞机高度不变。
x
n
x_n
xn 表示飞行器在
n
n
n 时的航程,雷达以恒定频率向目标发射追踪波束,周期为
Δ
t
\Delta t
Δt,可以用以下两个方程描述运动:
x
n
+
1
=
x
n
+
Δ
t
x
˙
n
x
˙
n
+
1
=
x
˙
n
x_{n+1}=x_n+\Delta t\dot{x}_n\\ \dot{x}_{n+1}=\dot{x}_n
xn+1=xn+Δtx˙nx˙n+1=x˙n
以上的方程组可以称为状态外推方程(State Exploration Equation)/过渡方程/预测方程,也是卡尔曼滤波的方程之一。
设定雷达跟踪周期
Δ
t
\Delta t
Δt 为5秒,假设在
n
−
1
n-1
n−1 时无人机估计航程30000m,估计速度40m/s。可以外推预测
n
n
n 时目标位置和速度值:
x
^
n
,
n
−
1
=
x
^
n
−
1
,
n
−
1
+
Δ
t
x
˙
^
n
−
1
,
n
−
1
=
30000
+
5
∗
40
=
30200
m
x
˙
^
n
,
n
−
1
=
x
˙
^
n
−
1
,
n
−
1
=
40
m
/
s
\hat{x}_{n,n-1}=\hat{x}_{n-1,n-1}+\Delta t\hat{\dot{x}}_{n-1,n-1}=30000+5*40=30200m\\\ \\ \hat{\dot{x}}_{n,n-1}=\hat{\dot{x}}_{n-1,n-1}=40m/s
x^n,n−1=x^n−1,n−1+Δtx˙^n−1,n−1=30000+5∗40=30200m x˙^n,n−1=x˙^n−1,n−1=40m/s
如果在
n
n
n时雷达测量航程(
z
n
z_n
zn)为30110,与预测值存在90m的偏差,可能有雷达测量误差、飞行器速度误差两方面因素导致.
下面写下飞行器速度的状态更新方程:
x
˙
^
n
=
x
˙
^
n
,
n
−
1
+
β
(
z
n
−
x
^
n
,
n
−
1
Δ
t
)
\hat{\dot{x}}_{n}=\hat{\dot{x}}_{n,n-1}+\beta(\frac{z_n-\hat{x}_{n,n-1}}{\Delta t})
x˙^n=x˙^n,n−1+β(Δtzn−x^n,n−1)
这里的系数
β
\beta
β 值取决于雷达精度:
(1)如果雷达精度高,倾向于是飞行器速度变化导致航程的测量偏差,则将
β
\beta
β调高。
(2)如果雷达精度低,倾向于是雷达测量误差导致航程的测量偏差,则将
β
\beta
β调低。
下面再写出飞行器位置的状态更新方程:
x
^
n
,
n
=
x
^
n
,
n
−
1
+
α
(
z
n
−
x
^
n
,
n
−
1
)
\hat{x}_{n,n}=\hat{x}_{n,n-1}+\alpha(z_n-\hat{x}_{n,n-1})
x^n,n=x^n,n−1+α(zn−x^n,n−1)
同样,这里的系数
α
\alpha
α 值取决于雷达精度,
α
\alpha
α 在 0~1 之间,
α
=
1
\alpha=1
α=1,则估计航程等于测量航程,
α
=
0
\alpha=0
α=0,则测量没有意义。
由此得到雷达追踪器的状态更性方程组,也被称为
α
−
β
\alpha-\beta
α−β 轨迹更新方程/
α
−
β
\alpha-\beta
α−β 轨迹滤波方程。
α
,
β
\alpha,\beta
α,β的值取决于测量精度,在0~1之间,对精度越高的设备,测量权重越高,此时滤波器会对目标速度变化作出快速响应;而如果精度较低,则采用低
α
、
β
\alpha、\beta
α、β,降低测量中的不确定性。
注:有些教材中 α − β \alpha-\beta α−β 滤波被写为 g-h 滤波。
一维空间中追踪加速飞行器
设定一架战斗机先以50m/s的恒定速度飞行15秒,然后以 8 m / s 2 8 m/s^2 8m/s2的加速度匀加速飞行35秒。


使用 α − β \alpha-\beta α−β 滤波器进行追踪,通过每次周期的速度估计考虑加速度带来的影响,会看到真实值或测量值与估计值之间存在一个固定的差值,被称为滞后误差(lag error),它的其他常见名称还有:动态误差、系统误差、偏移误差、截断误差。
因此需要使用 α − β − γ \alpha-\beta-\gamma α−β−γ 滤波器进行跟踪,将目标加速度考虑进去:
状态外推方程变为:
x
^
n
+
1
,
n
=
x
^
n
,
n
+
x
˙
^
n
,
n
Δ
t
+
x
¨
^
n
,
n
Δ
t
2
2
x
˙
^
n
+
1
,
n
=
x
˙
^
n
,
n
+
x
¨
^
n
,
n
Δ
t
x
¨
^
n
+
1
,
n
=
x
¨
^
n
,
n
\hat{x}_{n+1,n}=\hat{x}_{n,n}+\hat{\dot{x}}_{n,n}\Delta t+\hat{\ddot{x}}_{n,n}\frac{\Delta t^2}{2}\\\ \\ \hat{\dot{x}}_{n+1,n}=\hat{\dot{x}}_{n,n}+\hat{\ddot{x}}_{n,n}\Delta t\\\ \\ \hat{\ddot{x}}_{n+1,n}=\hat{\ddot{x}}_{n,n}
x^n+1,n=x^n,n+x˙^n,nΔt+x¨^n,n2Δt2 x˙^n+1,n=x˙^n,n+x¨^n,nΔt x¨^n+1,n=x¨^n,n
状态更新方程变为
x
^
n
,
n
=
x
^
n
,
n
−
1
+
α
(
z
n
−
x
^
n
,
n
−
1
)
x
˙
^
n
,
n
=
x
˙
^
n
,
n
−
1
+
β
(
z
n
−
x
^
n
,
n
−
1
Δ
t
)
x
¨
^
n
,
n
=
x
¨
^
n
,
n
−
1
+
γ
(
z
n
−
x
^
n
,
n
−
1
0.5
Δ
t
2
)
\hat{x}_{n,n}=\hat{x}_{n,n-1}+\alpha(z_n-\hat{x}_{n,n-1})\\\ \\ \hat{\dot{x}}_{n,n}=\hat{\dot{x}}_{n,n-1}+\beta(\frac{z_n-\hat{x}_{n,n-1}}{\Delta t})\\\ \\ \hat{\ddot{x}}_{n,n}=\hat{\ddot{x}}_{n,n-1}+\gamma(\frac{z_n-\hat{x}_{n,n-1}}{0.5\Delta t^2})
x^n,n=x^n,n−1+α(zn−x^n,n−1) x˙^n,n=x˙^n,n−1+β(Δtzn−x^n,n−1) x¨^n,n=x¨^n,n−1+γ(0.5Δt2zn−x^n,n−1)
包含加速度模型的
α
−
β
−
γ
\alpha-\beta-\gamma
α−β−γ 滤波器可以追踪匀加速运动的目标,并且消除滞后误差。



然而,真正的目标动态模型仍可能有很多不同的因素,使得 α − β − γ \alpha-\beta-\gamma α−β−γ 滤波器失效。
1.3 卡尔曼滤波
二、多维卡尔曼滤波
现实世界中的卡尔曼滤波都是多维的,这一部分介绍多维的卡尔曼滤波及其如何在矩阵中表示,涉及线性代数,将展示卡尔曼滤波的数学推导和动态系统模型,最终设计处一个多维的卡尔曼滤波算法。
三、扩展内容与现实问题
包括扩展卡尔曼滤波器、无迹卡尔曼滤波和在解决现实困难问题应用的卡尔曼滤波。