介绍
本文主要想解决基于聚类的概念漂移检测方法中常做出的强假设问题,即假设同类比较接近,异类比较远离,并且还假设新类别出现时通常会连续大量出现。
针对这些问题,本文提出了一种基于数据流的半监督自适应分类框架SACCOS,能够在概念漂移和概念进化的情况下进行标签预测。
主要贡献为:
- 提出了一个半监督框架,它使用基于图的聚类技术来解决概念漂移和概念进化问题
- 对数据流中的数据实例进行在线归一化,以统一其规模,并使用聚类集合在短时间内检测新类别
- 进行了实验
背景
这部分主要讲解了概念演化,其实就是新类的出现。但是新类的出现又分为两种情况:
- 一种是之前从未出现过这个类,也就是在时间 t > 0 t>0 t>0时出现了某一个类别所对应的实例,在 0 < t ′ < t 0<t^{\prime}<t 0<t′<t的时间内都没有出现过,模型也没有基于这个类的实例训练及更新过,这称为新类别的出现
- 一种是类别重新出现,即在 t > 0 t>0 t>0时出现了某一个类别,该类别在 0 < t ′ < t 0<t^{\prime}<t 0<t′<t内曾经出现过,而如果分类器的训练数据以及更新数据不包含这个重新出现的类别的实例,那么也可以认为它是新类别出现
因此形式上将这两种统一,即定义 t 0 、 t 1 t_0、t_1 t0、t1之间的概念演化为 P t 0 ( y ) ≠ P t 1 ( y ) P_{t_0}(y)\neq P_{t_1}(y) Pt0(y)=Pt1(y)
具体方法
问题描述
给定初始训练数据为 D = { ( x i , y i ) } i = 1 m D=\{(x_i,y_i)\}^m_{i=1} D={(xi,yi)}i=1m,其中 y i ∈ Y = { 1 , 2 , 3 , . . . , c } y_i\in Y=\{1,2,3,...,c\} yi∈Y={1,2,3,...,c}。而非平稳的流数据为 S = { ( x t ′ , y t ′ ) } t = 1 ∞ S=\{(x_t^{\prime}, y_t^{\prime})\}^{\infty}_{t=1} S={(xt′,yt′)}t=1∞,其中 y t ′ ∈ Y ′ = { 1 , 2 , . . . , c , c + 1 , . . . , c ′ } y_t^{\prime}\in Y^{\prime}=\{1,2,...,c,c+1,...,c^{\prime}\} yt′∈Y′={1,2,...,c,c+1,...,c′},代表在流数据中可能会出现新的类别。那么问题就是让分类器在时间 t t t和 t ′ t^{\prime} t′之间的流数据进行训练,其中的标签集合为 Y t t ′ ∈ Y ′ Y^{t^{\prime}}_t\in Y^{\prime} Ytt′∈Y′,那么当 t ′ ′ t^{\prime \prime} t′′时刻出现实例 x ′ ′ x^{\prime \prime} x′′其标签为 y ′ ′ y^{\prime \prime} y′′,判断其是否属于 Y t t ′ Y^{t^{\prime}}_t Ytt′。该问题的主要挑战为概念漂移的发生、短时间内多个新兴类别的出现以及类别标签的有限可用性。
概述
具体算法文字描述为:
- 首先,SACCOS从已知类别标签的实例创建聚类的初始集合,并训练分类器来检测现有类别
- 其次,对于流数据,沿着每个新实例执行在线归一化以统一其特征的尺度
- 然后将标准化后的实例临时存储在动态缓冲器W中,并使用聚类集成来识别该实例是否为离群值(它是否落在集成的边界之外)
- 如果不是则用分类器来预测其标签,如果是则临时存储在异常值缓冲器B中
- 一旦B中数目超过临界值,那么就使用新兴类检测模块,通过互图聚类对这些离群值进行聚类
- 聚类完成后,用现有的分类器对这些离群值的每个集成的每个实例都进行预测,并且计算其置信度,而一个集群的置信度是其中所有实例置信度的最低值。
- 当集群的置信度高于阈值,那么该集群内的实例就按照现有分类器之前为它们预测所带来的伪标签,作为其分类结果;如果集群的置信度小于阈值,那么将从该集群中随机采样一个实例并请求其真实标签,再通过标签传播以预测集群中其他实例的标签
- 最后,SACCOS使用在线变化点检测(CPD)机制来检测分类器置信度在预测现有类实例的标签时的变化,当发生改变时(意味着发生了概念漂移),则使用最近沿着流观察到的实例训练的另一个分类器来替换该分类器
这里补充一下标签传播标签传播是一种基于图的半监督学习方法,用于聚类问题。其基本原理是利用已知标签的样本来传播标签,以此来为未知样本预测标签。具体来说,将已知标签的样本看作是带标签的节点,未知样本看作是未标记的节点,可以将它们组成一个图,其中节点代表样本,边代表样本之间的相似性关系。这个相似性关系可以用一些相似性度量方法来计算,比如欧氏距离、余弦相似度等等。标签传播方法的基本思路是:首先将带标签的节点的标签向它的邻居节点传播,然后更新未标记节点的标签,重复这个过程直到收敛。传播的过程中,节点的标签会受到相邻节点的标签影响,因此节点的标签不断地被修正,最终收敛到一个稳定的状态。用公式表示为:
f
i
=
∑
j
∈
N
i
w
i
j
f
j
∑
j
∈
N
i
w
i
j
f_i=\frac{\sum_{j\in N_i}w_{ij}f_j}{\sum_{j\in N_i}w_{ij}}
fi=∑j∈Niwij∑j∈Niwijfj
即节点i的标签为其邻居标签的加权和。
具体框架
初始化
该阶段,首先对实例进行归一化,然后采用其中的带标签实例来训练分类器C。接着使用归一化的初始数据生成聚类集合,并将其添加到聚类集成M中,因此这就形成了初始的分类器以及聚类集成。那么M有大小限制,为 T M T_M TM。
在预热期后,对于出现的每个新数据实例,都将其保存在临时数据缓冲器S中,其大小为 T S T_S TS。每当S满了,SACCOS就更新规范化参数并规划范S中的那些实例,再将这些实例发送到其他模块进行下一步处理,然后清理S
在线归一化(标准化)
聚类机制通常需要依赖一个好的特征空间来测量组实例的距离,那么如果特征属于一个无界的范围那么将是失败的算法,因此通常需要进行标准化实例数据集来克服以上问题。但是流数据通常是具有未知分布的因此很难对特征进行归一化,因此采取在线归一化。
假设之前已经观察到了N个实例,那么当前从S发送过来新的 T S T_S TS个实例,那么对于均值和方差的更新为:


而因为新来了样本,那么当前聚类的各个簇的质心和半径也应该发生相应的变化,即:

聚类
采用的算法为多图聚类(MGC),其已经被证明是特别有效识别重要集群的方法。
首先进行如下定义:
- KNN-set:关于实例 x i x_i xi的最近的k个邻居实例
- 互图G(k):在图中任意两个相邻节点 x 1 、 x 2 x_1、x_2 x1、x2必定都是彼此的KNN-set中的实例
- 互图的增长:假设 x 1 ∈ G 1 ( k ) , x 2 ∈ G 2 ( k ) x_1\in G_1(k),x_2\in G_2(k) x1∈G1(k),x2∈G2(k),如果 x 1 、 x 2 x_1、x_2 x1、x2是彼此的KNN-set中的实例,那么可以将其连接,也就可以将 G 1 , G 2 G_1,G_2 G1,G2连接为更大的图
那么每个图对应的聚类可以表示为:

G ( k , D ) G(k,D) G(k,D)代表数据集D的所有互图的集合,而 V ( G l ( k ) ) V(G_l(k)) V(Gl(k))代表图的顶点集,顶点代表实例,因此由实例组成聚类的簇。
而为了并行的处理提高效率,其通过KD-Tree将数据实例的特征空间划分为基于特征方差的子空间,这里每个子空间最多包含
N
m
N_m
Nm个实例。在每个子空间中首先计算其中每个数据实例的q邻域噪声系数(q-NNC)来执行噪声降低,即定义
D
~
q
,
n
e
a
r
e
s
t
\tilde{D}_{q,nearest}
D~q,nearest和
D
~
q
,
f
a
r
t
h
e
s
t
\tilde{D}_{q,farthest}
D~q,farthest为对于实例x的q个最近邻居的平均距离和q个最远邻居的平均距离,然后计算其q-NNC系数为:
q
−
N
N
C
(
x
)
=
D
~
q
,
n
e
a
r
e
s
t
(
x
)
D
~
q
,
f
a
r
t
h
e
s
t
(
x
)
q-NNC(x)=\frac{\tilde{D}_{q,nearest}(x)}{\tilde{D}_{q,farthest}(x)}
q−NNC(x)=D~q,farthest(x)D~q,nearest(x)
越接近于1,认为其更可能是噪声实例。因此将该子空间的实例按照q-NNC系数降序排序,接着就是确定阈值,将系数大于阈值的实例认为是噪声从而将其丢弃。那么阈值的确定方法为最小标准差的差值来确定,即假设阈值为
T
n
o
i
s
e
T_{noise}
Tnoise,将实例分为了两部分,那么就是让这两部分的方差的差的绝对值最小,即:
T
n
o
i
s
e
=
a
r
g
m
i
n
∣
σ
(
L
r
)
−
σ
(
L
l
)
∣
T_{noise}=argmin\vert \sigma(L^r)-\sigma(L^l)\vert
Tnoise=argmin∣σ(Lr)−σ(Ll)∣
接下来,就是利用MGC建立多个聚类,每个聚类簇形成一个球形超平面,其质心为其中实例的每个特征的平均值,其半径是平均距离,具体算法为:

具体的算法流程图为:





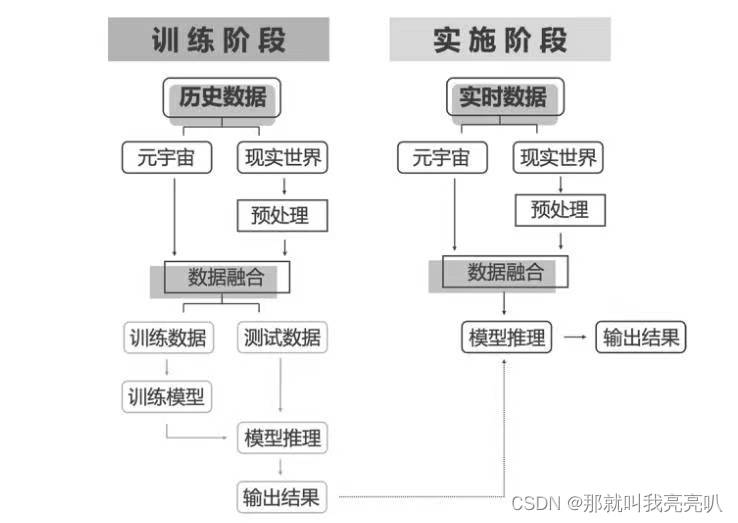
![[架构之路-123]-《软考-系统架构设计师》-操作系统-2-操作系统原理 - 存储层次结构与存储管理(寄存器、Cache、MMU、内存、外存、页表)](https://img-blog.csdnimg.cn/img_convert/a8e24d9bdaaa34796153ad055953d35e.png)