目录

极限的定义：

 数列极限的几何意义：

由极限的定义得出的极限的两个结论：

 ​编辑

极限的第三个结论：

 例题

方法1： ​编辑

方法2： ​编辑

方法3：

​编辑 

---

极限的定义：

 如何理解呢？

极限的通俗理解：

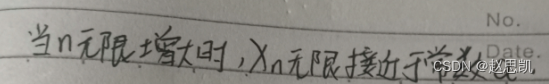
 用数列的语言来说：

当数列的项数n无限增大时，数列的项要多接近就有多接近与a。

 我们如何理解？

答：首先，我们要清楚，极限是一个无限的过程，对于无限的过程，我们要以有限的形式进行表达，上图就是我们对于极限的有限表达。

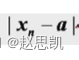
 |Xn-a|是什么意思？

答：首先要清楚Xn的意思是数列的第n项，a表示我们的极限值，所以 |Xn-a|表示我们数列的项和极限值的接近程度。

 这是什么意思？

答：

 为什么要使用'任意'符号？

答:

这里是什么意思？

答：存在N，让N以后的项无限接近于常数a，这个N其实是不存在的，因为极限是一个无限的过程，我们假设N存在，N之后的元素是无限接近于常数a的，所以N只是用来刻画n无限增大以至于无限接近于常数a的这个过程。

 数列极限的几何意义：

等价于：

 

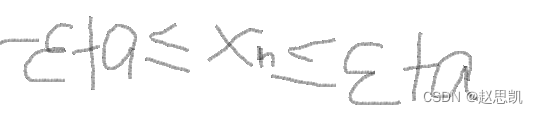
 这时候就形成一个领域：

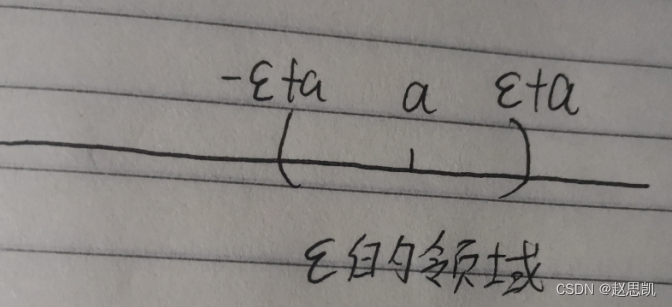
 我们可以把N当作数列有限项与无限项的分割线：

 在N之后的数列中的项是放在领域之内的：

 在领域中的无限项表示无限接近于极限值a。

 一句话总结数列极限的定义：

由极限的定义得出的极限的两个结论：

 

 我们对结论1进行阐述：

答：a表示我们数列的极限，当b<a时，也就是b小于数列的极限，存在N，这个N之后的无限项全部无限接近于a值，所以当n大于N时，对应的项全部无限接近于a值，而b<a，则N之后所有的项都大于b。

我们对结论2进行阐述：

答：a表示数列的极限，当c>a时，也就是c大于数列的极限，所以N之后的无限项全部无限接近于a值，但是比a值小，因为c值比a值大，所以N之后的无限项全部小于c值。

极限的第三个结论：

数列Xn的极限与数列的前n项无关。

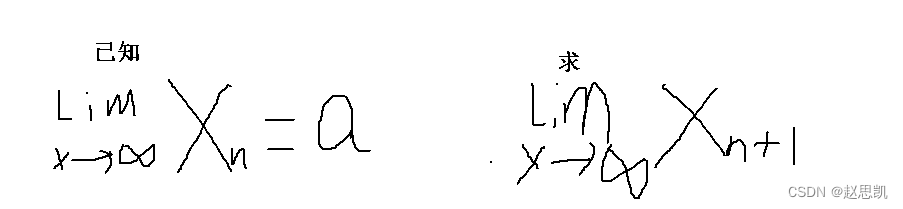
 Xn+1相当于去掉了数列的第一项，数列的第一项并不影响我们的极限值。

所以：

 我们之前知道一个结论：单调有界一定有极限。

单调有界不一定要从第一项就开始单调，在某一段区间上单调他也有极限。

例题1：

结果依然为1，因为右式是数列Xn的奇数部分，也是原来数列的部分项，所以又叫右式为数列Xn的奇数列。

奇数列和偶数列都是原来数列的部分项，所以奇数列和偶数列的极限也等于原数列的极限值a。

所以数列有极限可以推导出数列的奇数列和偶数列都有极限，但是数列的奇数列或者偶数列都有极限可以推导出数列有极限吗？

答：并不能，例如：

 数列的奇数列为：

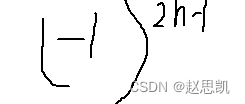
奇数列全为-1，所以奇数列的极限值也为-1.

数列的偶数列为： 

 

 偶数列全为1，所以偶数列的极限值也为1.

虽然奇数列和偶数列都有极限值，但是他们的极限值不同，所以无法推导出数列有极限。

当奇数列和偶数列都有极限值，并且奇数列和偶数列的极限值相同的情况下==>数列有极限。

答：因为奇数列和偶数列虽然是数列的部分列，但是这两个部分列的集合包括了数列的所有项，所有的项的极限值都以a为极限，则该数列的极限值为a。

 例题

方法1： 

方法2： 

方法3：