刚看到题的时候是懵的，这也太长了。到底是要表达什么呢。
不妨把这个矩阵看成一个正方形的图片，想象你在处理图片，从整体逐步到局部。

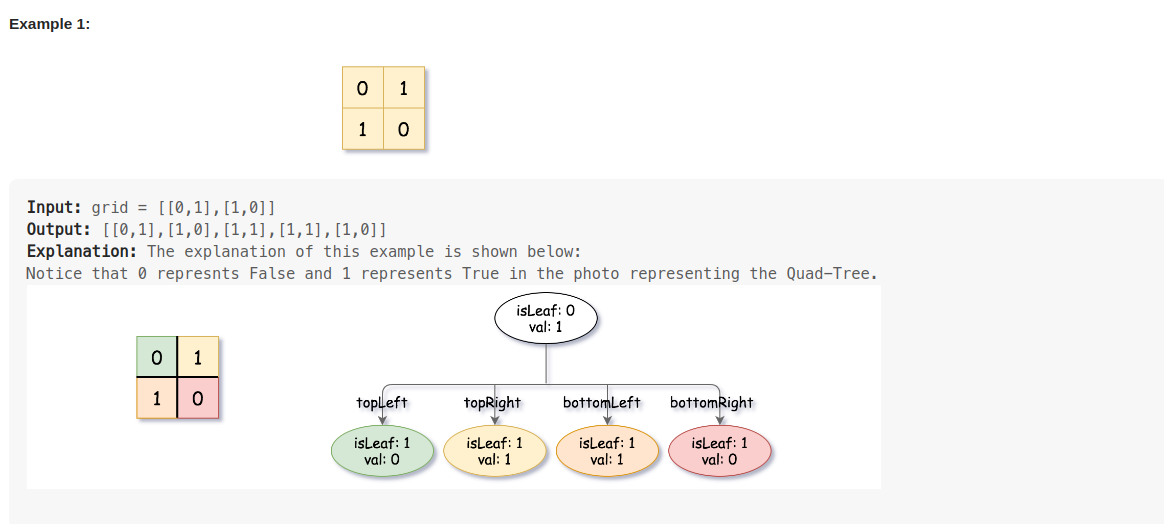
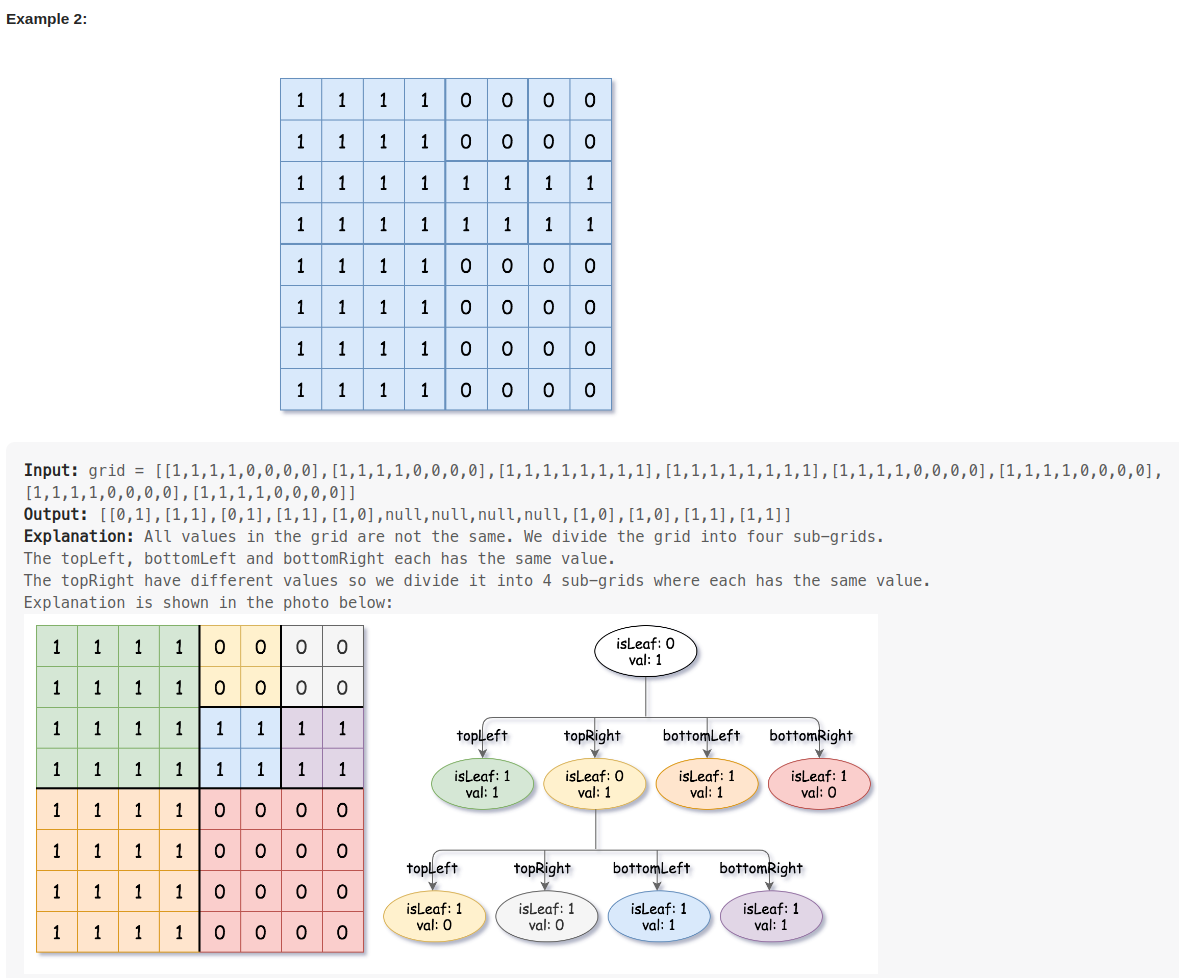
刚开始看一整张图片，如果是全0或全1，这个就是叶子节点，怎么表达叶子节点呢，就是isLeaf=true, val=0 or 1(全0 or 全1)，
这个isLeaf和val会组成一个Node.

如果不是全0或全1，那就不是叶子节点，就要把图片等分成4块，左上的一块叫topLeft, 右上的一块叫topRight,
同理bottomLeft, bottomRight,
这4块按同样的方法再进入下一轮：
全0或全1就是叶子节点，否则再细分成4小块，再处理。
不是叶子节点时，isLeaf=false, val=0 or 1都行，这里统一为1.

最后返回四叉树的根。

思路：

分而治之。

简单看下流程吧：
首先一整个矩阵，判断是否全0或全1，
是：叶子节点(isLeaf = true, val=0 or 1), 返回这个节点。
否：建立当前节点作为root(isLeaf = false, val = 1),
然后把矩阵等分成4小块，分别把左上，右上，左下，右下四小块返回的结果给root.topLeft, root.topRight …

每个小块的处理过程重复上面的步骤。
至于怎么分成小块，已知每个小块的左上角坐标(r,c)和边长，又知grid, 就可取出对应的小块。

树的节点建立有点类似于树的前序遍历。

class Solution {
    public Node construct(int[][] grid) {
        int n = grid.length;
        return buildNode(grid, 0, 0, n);
    }

    Node buildNode(int[][] grid, int r, int c, int len) {
        if(allSame(grid, r, c, len))
            return new Node(grid[r][c] == 1 ? true : false, true);
        
        Node root = new Node(true, false);
        root.topLeft = buildNode(grid, r, c, len/2); //矩阵起点的(r,c)和边长
        root.topRight = buildNode(grid, r, c+len/2, len/2);
        root.bottomLeft = buildNode(grid, r+len/2, c, len/2);
        root.bottomRight = buildNode(grid, r+len/2, c+len/2, len/2);
        return root;
    }

    boolean allSame(int[][] grid, int r, int c, int len) {
        int cur = grid[r][c];
        for(int i = r; i < r + len; i++) {
            int[] cols = grid[i];  //一维数组比二维数组高效
            for(int j = c; j < c + len; j++) {
                if(cols[j] != cur) return false;
            }
        }
        return true;
    }
}