树的导览
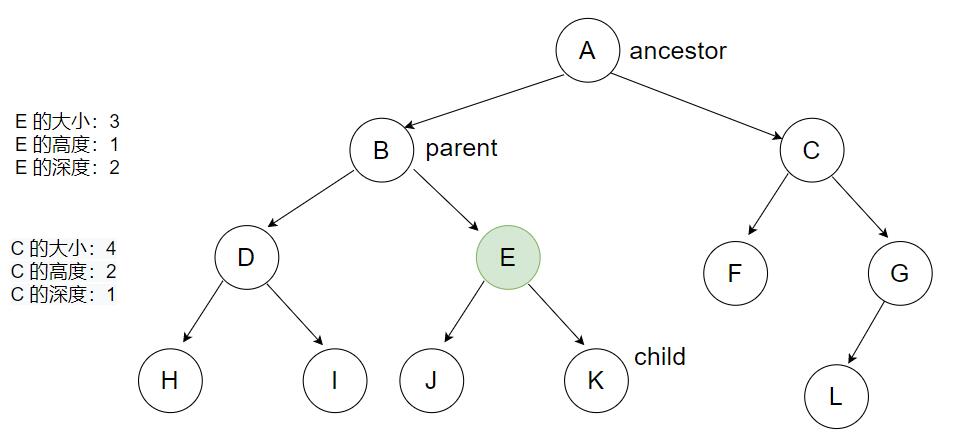
树由节点(nodes)和边(edges)构成,如下图所示。整棵树有一个最上端节点,称为根节点(root)。每个节点可以拥有具有方向的边(directed edges),用来和其他节点相连。相连的节点之中,在上者称为父节点(parent),在下者称为子节点(child)。
一些基本概念:
- 节点的度:一个节点含有的子树的个数,如果最多只允许两个子节点,即为二叉树
- 叶节点:无子节点,即度为 0 的节点称为叶节点
- 兄弟节点:不同的节点拥有相同的父节点
- 路径长度:根节点到任何节点之间有唯一路径,路径所经过的边数
- 节点的深度:根节点到任一节点的路径长度,根节点的深度永远为 0
- 节点的高度:某节点到其叶节点的路径长度
二叉搜索树的概念
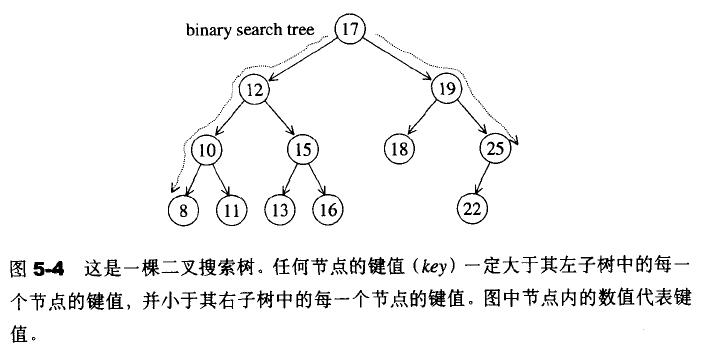
二叉搜索树可以提供对数时间的元素插入和访问,是一种特殊的二叉树,具有以下规则:
- 任何节点的键值一定大于其左子树中的每一个节点的键值
- 任何节点的键值一定小于其右子树中的每一个节点的键值
因此二叉搜索树的最左节点是最小元素,最右节点是最大元素。
二叉搜索树的实现
节点的定义
该节点设计很简单:
- 包含三个成员变量:节点值、左孩子指针、右孩子指针
- 构造函数:将成员变量初始化
/// @brief 二叉树的节点
/// @tparam K 节点值的类型
template<class K>
struct BSTreeNode {
BSTreeNode(const K& key = K())
: _key(key)
, _left(nullptr)
, _right(nullptr)
{}
K _key; // 节点值
BSTreeNode<K>* _left; // 左指针
BSTreeNode<K>* _right; // 右指针
};
接口总览
文章完整代码:BinarySearchTree · 秦国维/data-structure
template<class K>
class BSTree {
typedef BSTreeNode<K> Node;
public:
Node* Find(const K& key);
Node* _FindR(Node* _root, const K& key);
Node* FindR(const K& key);
bool Insert(const K& key);
bool _InsertR(Node*& _root, const K& key);
bool InsertR(const K& key);
bool Erase(const K& key);
bool _EraseR(Node*& root, const K& key);
bool EraseR(const K& key);
private:
Node* _root = nullptr;
};
查找
根据二叉搜索树的特性,可以在二叉搜索树快速的找到指定值:
- 若 key 值大于当前节点的值,在当前节点的右子树中查找
- 若 key 值小于当前节点的值,在当前节点的左子树中查找
- 若 key 值等于当前节点的值,返回当前节点的地址
- 若找到空,查找失败,返回空指针
非递归
/// @brief 查找指定 key 值
/// @param key 要查找的 key
/// @return 找到返回节点的指针,没找到返回空指针
Node* Find(const K& key) {
Node* cur = _root;
while (cur != nullptr) {
// key 值与当前节点值比较
if (key > cur->_key) {
cur = cur->_right;
} else if (key < cur->_key) {
cur = cur->_left;
} else {
return cur;
}
}
return nullptr;
}
递归
Node* _FindR(Node* root, const K& key) {
if (root == nullptr) {
return nullptr;
}
// key 值与当前节点值比较
if (key > root->_key) {
// key 值大于当前节点的值,递归到右子树查找
return _FindR(root->_right, key);
} else if (key < root->_key) {
// key 值小于当前节点的值,递归到左子树查找
return _FindR(root->_left, key);
} else {
return root;
}
}
Node* FindR(const K& key) {
return _FindR(_root, key);
}
插入
根据二叉搜索树的性质,插入操作也很简单:
- 如果是空树,将插入的节点作为根节点
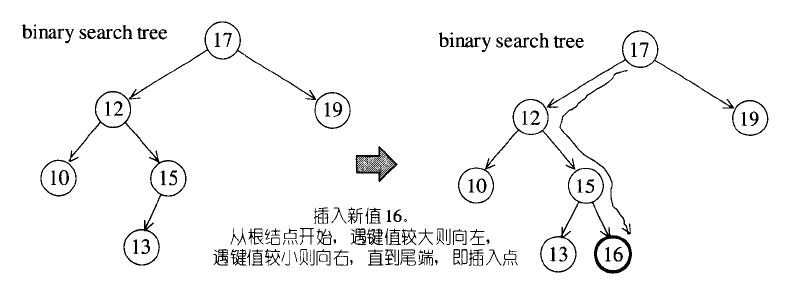
- 如果不是空树,利用性质找到该插入的位置,将节点插入
插入新元素时,从根节点开始,遇到键值较大的就向左,遇到键值较小的就向右,一直到尾端,即为插入点。
非递归
使用非递归插入函数时,需要定义一个 parent 指针,该指针用来指示插入节点的父节点,以便将新节点插入。
/// @brief 在二叉搜索树中插入指定节点
/// @param key 节点的 key 值
/// @return 成功返回 true,失败返回 false
bool Insert(const K& key) {
if (_root == nullptr) {
// 第一个插入的节点,构建为根
_root = new Node(key);
return true;
}
// 先找到要插入的位置
Node* parent = nullptr;
Node* cur = _root;
while (cur != nullptr) {
if (key > cur->_key) {
parent = cur;
cur = cur->_right;
} else if (key < cur->_key) {
parent = cur;
cur = cur->_left;
} else {
// 已经有该值了,插入失败
return false;
}
}
// 创建要插入的节点
cur = new Node(key);
// 看插入节点在父节点哪边
if (key > parent->_key) {
parent->_right = cur;
} else {
parent->_left = cur;
}
return true;
}
递归
递归版本的插入相对于非递归版本更简单,要注意的是 Node* 参数一定要传引用,这样才能改变父亲指针的指向。
bool _InsertR(Node*& _root, const K& key) {
if (_root == nullptr) {
// 因为传递的是引用,所以可以直接改变指向
_root = new Node(key);
return true;
}
// 判断 key 与当前节点值大小关系
if (key > _root->_key) {
// key 更大就递归到右子树插入
return _InsertR(_root->_right, key);
} else if (key < _root->_key) {
// key 更小就递归到左子树插入
return _InsertR(_root->_left, key);
} else {
return false;
}
return false; // 为了消除编译警告
}
bool InsertR(const K& key) {
return _InsertR(_root, key);
}
删除
删除相对与插入就复杂的多了,需要考虑三种情况:
- 待删除节点没有子树
- 待删除节点有一个子树
- 待删除节点有两个子树
下面就来讨论这三种情况:
待删除节点没有子树
这种情况比较简单,直接将指向该节点的指针置空即可。
待删除节点有一个子树
如果节点 Q 只有一个子节点,就直接将 Q 的子节点连至 Q 的父节点,并将 Q 删除。

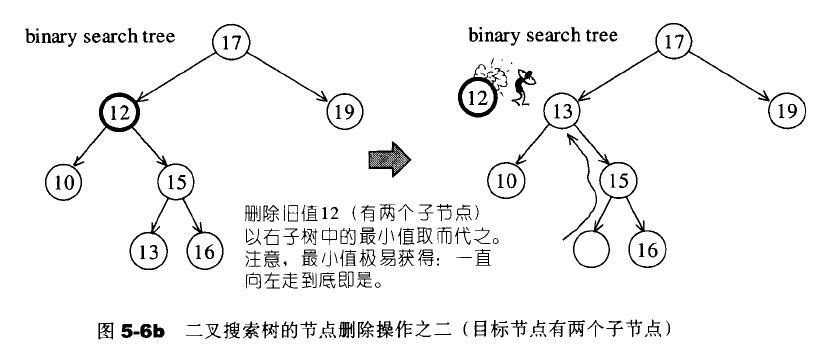
待删除节点有两个子树
这时就比较复杂了,需要使用替换法。如果 Q 有两个节点,就以右子树的最小节点取代 Q(左子树的最大节点也可以)。
右子树最小节点获取方法:从右子节点开始,一直向左找到底。
为什么右子树最小节点可以替换当前节点?
因为右子树最小节点一定大于当前节点左子树中的所有节点,又一定小于右子树中的其他节点,故不会破坏二叉搜索树的规则。
非递归
该实现版本同样需要定义一个 parent 指针,以便将其孩子托付给父亲。
/// @brief 在二叉搜索树中删除指针节点
/// @param key 删除节点的 key
/// @return 删除成功返回 true,失败返回 false
bool Erase(const K& key) {
Node* parent = nullptr;
Node* cur = _root;
// 先找要删除节点的位置
while (cur != nullptr) {
if (key > cur->_key) {
// 大于就到右子树中找
parent = cur;
cur = cur->_right;
} else if (key < cur->_key) {
// 小于就到左子树中找
parent = cur;
cur = cur->_left;
} else {
// 找到要删除的节点了
if (cur->_left == nullptr) {
// cur 左孩子为空,即只有一个右孩子或没有孩子
if (parent == nullptr) {
// 如果要删除的是根节点,更换新根
_root = _root->_right;
} else {
if (parent->_left == cur) {
parent->_left = cur->_right;
} else {
parent->_right = cur->_right;
}
}
// 释放掉 cur 指向的空间
delete cur;
cur = nullptr;
} else if (cur->_right == nullptr) {
// 此时说明只有左孩子
if (parent == nullptr) {
// 如果要删除的是根节点,更换新根
_root = _root->_left;
} else {
if (parent->_left == cur) {
parent->_left = cur->_left;
} else {
parent->_right = cur->_left;
}
}
// 释放掉 cur 指向的空间
delete cur;
cur = nullptr;
} else {
// 此时有左右孩子,需要使用替换法删除
Node* minParent = cur;
Node* min = cur->_right;
// 先找到右子树的最左节点
while (min->_left != nullptr) {
minParent = min;
min = min->_left;
}
// 将最小节点的值替换到 cur 上
cur->_key = min->_key;
if (minParent->_left == min) {
// 最小节点位于父节点的左边,将它的右子树托付给父节点
minParent->_left = min->_right;
} else {
// 最小节点位于父节点的右边,这时就是 cur 的右子树没有左子树
// minNode->_left 一定为空,写成这样比较对称
minParent->_right = min->_left;
}
delete min;
min = nullptr;
} // end of if (cur->_left == nullptr)
return true;
} // end of if (key > cur->_key)
} // end of while (cur != nullptr)
// 没找到要删除的节点,返回 false
return false;
}
递归
递归版本的删除相对于非递归版本更简单,要注意的是 Node* 参数一定要传引用,这样才能改变父亲指针的指向,将节点删除。
bool _EraseR(Node*& root, const K& key) {
if (root == nullptr) {
// 没找到要删除的节点返回 false
return false;
}
if (key > root->_key) {
// key 更大就到右子树中删除
_EraseR(root->_right, key);
} else if (key < root->_key) {
// key 更小就到左子树中删除
_EraseR(root->_left, key);
} else {
Node* del = root;
if (root->_left == nullptr) {
// 此时左为空或左右为空,只需要将右子树给父节点即可
// 左右为空时,右子树为空,不会违反规则
root = root->_right;
} else if (root->_right == nullptr) {
// 此时右为空,只需要将左子树给父节点
root = root->_left;
} else {
// 有两个孩子,需要替换法删除
Node* min = root->_right;
while (min->_left != nullptr) {
min = min->_left;
}
// 把最小的节点的值换上
root->_key = min->_key;
// 递归到右子树,将 minnode 删掉
// 一定要 return,否则会重复释放
return _EraseR(root->_right, min->_key);
}
delete del;
del = nullptr;
return true;
}
return false; // 为了消除编译警告
}
bool EraseR(const K& key) {
return _EraseR(_root, key);
}