文章目录
- 1、简介
- 1.1 何为卡特兰数
- 1.2 卡特兰数的通项公式
- 2、应用
- 2.1 题目1:括号合法
- 题目描述
- 思路分析
- 2.2 题目2:进出栈的方式
- 2.2.1 题目描述
- 2.2.2 思路分析
- 2.3 题目3:合法的序列
- 2.3.1 题目描述
- 2.3.2 思路分析
- 2.3.3 代码实现
- 2.4 题目4:不同二叉树的数量
- 2.4.1 题目描述
- 2.4.2 思路分析
- 2.4.3 代码实现
- 3、总结
1、简介
1.1 何为卡特兰数
卡特兰数又称卡塔兰数,英文名Catalan number,是组合数学 中一个常在各种计数问题中出现的数列。
前几项为:1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 6564120420, 24466267020, 91482563640, 343059613650, 1289904147324, 4861946401452, …
1.2 卡特兰数的通项公式
k ( 0 ) = 1 , k ( 1 ) = 1 k(0) = 1, k(1) = 1 k(0)=1,k(1)=1 时,如果接下来的项满足:
k ( n ) = k ( 0 ) ∗ k ( n − 1 ) + k ( 1 ) ∗ k ( n − 2 ) + . . . + k ( n − 2 ) ∗ k ( 1 ) + k ( n − 1 ) ∗ k ( 0 ) k(n) = k(0) * k(n - 1) + k(1) * k(n - 2) + ... + k(n - 2) * k(1) + k(n - 1) * k(0) k(n)=k(0)∗k(n−1)+k(1)∗k(n−2)+...+k(n−2)∗k(1)+k(n−1)∗k(0)
或者
k ( n ) = C 2 n n − C 2 n n − 1 k(n) = C_{2n}^n- C_{2n}^{n-1} k(n)=C2nn−C2nn−1
或者
k ( n ) = C 2 n n / ( n + 1 ) k(n) = C_{2n}^n / (n + 1) k(n)=C2nn/(n+1)
就说这个表达式,满足卡特兰数,常用的是范式1和2,3几乎不会使用到
2、应用
2.1 题目1:括号合法
题目描述
给定 N N N 个左括号, N N N 个右括号,它们自由组合,必须全部使用,能得到多少个合法的组合?
思路分析
“合法”的定义是对于自由排列的组合,只要保证任意的前缀,右括号数量 ≤ \le ≤ 左括号数量,那么它最终一定是合法的。原理就是左括号比右括号多的时候,一旦出现右括号就能将多的左括号配对,最终一定会全部配对成功。反之则不行。
先讨论一个数学思想:如何确定两个集合相等
【集合A 和 集合B 可以是完全不相干的两个可数集合,只要能找到一个映射 f f f,使得A集合中的一个对应B集合中的一个,又能找到一个和 f f f 毫不相干的映射 g g g 使得 B集合中的一个对应 A集合中的一个,如果存在这样一组映射,那么A集合数量和B集合数量一定相等。】
借此,来讨论括号组合的合法问题。合法的组合数量不好算,那就可以先选出不合法的组合数量,然后使用总的排列方法 减去 不合法的,就是合法的。
总的排列方法数为 C 2 n n C_{2n}^n C2nn,意思是一共 2 n 2n 2n 个位置,选择其中的 n n n 个放左括号,剩下的 n n n 个位置放右括号。
而不合法的特征一定存在一个最初的前缀:右括号数量 = 左括号数量 + 1,如 ())((),最初前缀就是 ())。那么在该前缀后的就是 右括号数量 + 1 = 左括号数量 (因为左右括号的数量相等)。以这个最初前缀为分界线,后面的所有括号进行反转,即右括号变成左括号,左括号变成右括号,就变成了())))(,那么分界线后的左括号数量 + 1 = 右括号数量。如此一来,整体的 右括号数量 = 左括号数量 + 2。
定义两个集合,A集合放所有不合法的情况,B集合是
n
+
1
n + 1
n+1 个右括号,
n
−
1
n-1
n−1个左括号 组合得到的所有情况 (该集合的来源不深究),也就是说通过上面的括号反转,A集合中任意一个不合法的元素通过该映射都能变出一个B集合的某一个元素;而B集合中的每个元素都能变成A集合其中的一个,如))))((,最初的不合法前缀为),以该前缀为分界线后面的所有括号反转。最终得到)((())。
所以 “ n n n 个左括号 和 n n n 个右括号组合不合法的数量” = “ n + 1 n+1 n+1个右括号 和 n − 1 n-1 n−1个左括号组合的所有数量”,即 C 2 n n + 1 C_{2n}^{n+1} C2nn+1。
所以, n n n 个左括号和 n n n 个右括号组合的合法数量 = C 2 n n − C 2 n n + 1 C_{2n}^{n} - C_{2n}^{n+1} C2nn−C2nn+1,而 C 2 n n + 1 = C 2 n n − 1 C_{2n}^{n+1} = C_{2n}^{n-1} C2nn+1=C2nn−1,因此合法的组合数量也可以是 C 2 n n − C 2 n n − 1 C_{2n}^n - C_{2n}^{n-1} C2nn−C2nn−1。
也就是说,括号类型的违规可以转换为卡特兰数进行计算,因为 C 2 n n − C 2 n n − 1 C_{2n}^n - C_{2n}^{n-1} C2nn−C2nn−1 是卡特兰数的通项公式之一。
2.2 题目2:进出栈的方式
2.2.1 题目描述
n n n 个数字要进出栈,一共有多少种进出栈的方式?
2.2.2 思路分析
例如,给定数字[1, 2],进出栈的方式:
合法的情况:
1. 1进(↓),1出(↑),2进(↓),2出(↑)
2. 1进(↓),2进(↓),2出(↑),1出(↑)
只用记录箭头
不合法的情况:
1. ↑ ↑ ↓ ↓ (没有数字进栈是无法出栈的)
考察箭头组合的合法数量,这其实就是括号问题。进栈是左括号,出栈是右括号。合法的条件就是在任何时候,右括号数量不能大于左括号数量,也就是任意时刻出栈次数 ≤ \le ≤ 进栈次数就是合法的进出栈方式,就是卡特兰数。
再举个例子:某个公司的股票有上涨和下跌,问有多少种交易方式可以使得股票不会跌到X轴以下?
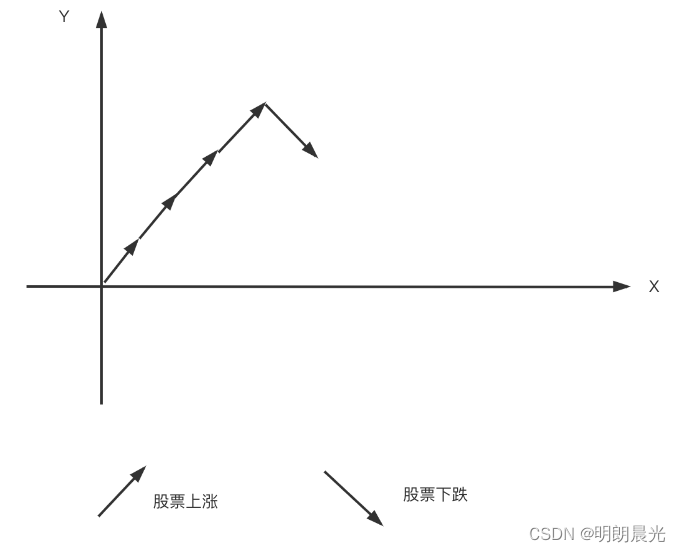
这也是一个卡特兰数问题,往上就是左括号,往下就是右括号,就是在问左右括号合理的结合方式。
2.3 题目3:合法的序列
2.3.1 题目描述
假设给你 N N N 个 0,和 N N N 个 1,你必须用全部数字拼序列。
返回有多少个序列满足:任何前缀串,1的数量都不少于0的数量
2.3.2 思路分析
这个就是 “括号合法” 模型问题,1是左括号,0是右括号,任意时刻满足左括号数量 ≥ \ge ≥ 右括号数量。
直接使用卡特兰数的通项公式解决即可。
2.3.3 代码实现
import java.util.LinkedList;
public class 10Ways {
//方法1:暴力递归
public static long ways1(int N) {
int zero = N;
int one = N;
LinkedList<Integer> path = new LinkedList<>();
LinkedList<LinkedList<Integer>> ans = new LinkedList<>();
process(zero, one, path, ans);
long count = 0;
for (LinkedList<Integer> cur : ans) {
int status = 0;
for (Integer num : cur) {
if (num == 0) {
status++;
} else {
status--;
}
if (status < 0) {
break;
}
}
if (status == 0) {
count++;
}
}
return count;
}
public static void process(int zero, int one, LinkedList<Integer> path, LinkedList<LinkedList<Integer>> ans) {
if (zero == 0 && one == 0) {
LinkedList<Integer> cur = new LinkedList<>();
for (Integer num : path) {
cur.add(num);
}
ans.add(cur);
} else {
if (zero == 0) {
path.addLast(1);
process(zero, one - 1, path, ans);
path.removeLast();
} else if (one == 0) {
path.addLast(0);
process(zero - 1, one, path, ans);
path.removeLast();
} else {
path.addLast(1);
process(zero, one - 1, path, ans);
path.removeLast();
path.addLast(0);
process(zero - 1, one, path, ans);
path.removeLast();
}
}
}
//方法2:卡特兰数的通项公式解决
public static long ways2(int N) {
if (N < 0) {
return 0;
}
if (N < 2) {
return 1;
}
long a = 1;
long b = 1;
long limit = N << 1;
for (long i = 1; i <= limit; i++) {
if (i <= N) {
a *= i;
} else {
b *= i;
}
}
return (b / a) / (N + 1);
}
public static void main(String[] args) {
System.out.println("test begin");
for (int i = 0; i < 10; i++) {
long ans1 = ways1(i);
long ans2 = ways2(i);
if (ans1 != ans2) {
System.out.println("Oops!");
}
}
System.out.println("test finish");
}
}
2.4 题目4:不同二叉树的数量
2.4.1 题目描述
有 N N N 个二叉树节点,每个节点彼此之间无任何差别。返回由 N N N 个二叉树节点,组成的不同结构数量是多少?
2.4.2 思路分析
如果 0 个节点,只能组成空树,1种;
如果 1 个节点,只能组成1个节点的树,1种;
如果 2 个节点,只有2种结构。
n 个节点组成二叉树的情况:
1)第 1 种划分:头结点1个,左子树0个,右子树
n
−
1
n-1
n−1 个
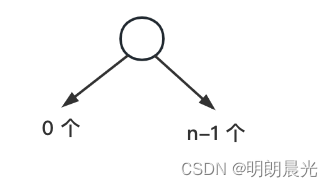
在这种划分下,不同结构的数量为:[0个节点组成的方法数]
×
\times
× [
n
−
1
n-1
n−1个节点组成的方法数]
2)第 2 种划分:头结点左边1个节点,右边
n
−
2
n-2
n−2 个节点
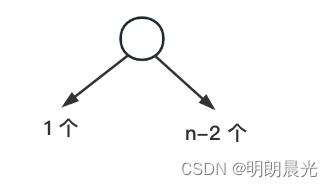
在这种划分下,不同结构的数量为:[1个节点组成的方法数]
×
\times
× [
n
−
2
n-2
n−2个节点组成的方法数]
这个规律就是卡特兰数的第1个通项公式,所以这就是卡特兰数。 那么直接用卡特兰数的第2个通项公式计算即可,因为卡特兰数的三个通项公式是等效的。
2.4.3 代码实现
public class DifferentBTNum {
// k(0) = 1, k(1) = 1
//
// k(n) = k(0) * k(n - 1) + k(1) * k(n - 2) + ... + k(n - 2) * k(1) + k(n - 1) * k(0)
// 或者
// k(n) = c(2n, n) / (n + 1)
// 或者
// k(n) = c(2n, n) - c(2n, n-1)
//方法1
public static long num1(int N) {
if (N < 0) {
return 0;
}
if (N < 2) {
return 1;
}
long[] dp = new long[N + 1];
dp[0] = 1;
dp[1] = 1;
for (int i = 2; i <= N; i++) {
for (int leftSize = 0; leftSize < i; leftSize++) {
dp[i] += dp[leftSize] * dp[i - 1 - leftSize];
}
}
return dp[N];
}
//方法2:卡特兰数
public static long num2(int N) {
if (N < 0) {
return 0;
}
if (N < 2) {
return 1;
}
long a = 1;
long b = 1;
for (int i = 1, j = N + 1; i <= N; i++, j++) {
a *= i;
b *= j;
long gcd = gcd(a, b);
a /= gcd;
b /= gcd;
}
return (b / a) / (N + 1);
}
public static long gcd(long m, long n) {
return n == 0 ? m : gcd(n, m % n);
}
public static void main(String[] args) {
System.out.println("test begin");
for (int i = 0; i < 15; i++) {
long ans1 = num1(i);
long ans2 = num2(i);
if (ans1 != ans2) {
System.out.println("Oops!");
}
}
System.out.println("test finish");
}
}
3、总结
- 要对卡特兰数的通项公式1和公式2烂熟于心;
- 对“括号合法”模型(左右括号数量相等的合法性问题)要有敏感度;
- 加强对卡特兰数通项公式1的敏感度的训练,如题目4,符合公式1等同于公式2,而通常可能是写出了暴力递归才会发现公式1,就要求对暴力解法有了解。
补充:
数学结论:所有整数和所有偶数数量相等。因为任何整数乘以2后等于某个偶数,而任意偶数除以2后等于某个整数,二者建立了一一映射关系,所以整数数量和偶数数量就是一样多的。在数学上,它叫作“等势”。
5米的线和10米的线上的点数量一样多。在两条线之外找某一个定点,5米线上找任意一个点和定点连线能对应到10米中的一个点,10米的任意一个点和定点连线能对应到5米中的一个点,所以5米的线和10米的线点一样多。
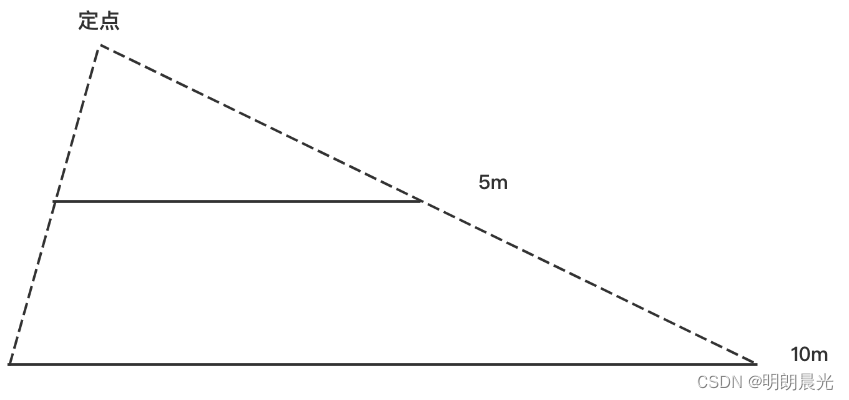
点是无长度的,无长度的东西有可能有无限个点。更多可以查看希尔伯特旅馆悖论。
总而言之,牵扯到一个非常重要的思想,两个可数集合A和B,能互相建立一种映射关系,那它们的数量就是一样多的。