算法设计与分析期末考试复习（六）

分支限界法

广度优先搜索：处理某顶点时，一次性发现其所有相邻顶点，未处理顶点加入等待队列
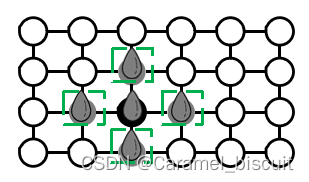
在这里插入图片描述
先来先服务：队尾加入，队首离开
o 加入队列，𝑸. Enqueue( )
o 离开队列，𝑸. Dequeue( )

分支限界法与回溯法的区别

回溯法的求解目标是找出解空间树中满足约束条件的所有解。
分支限界法的求解目标是尽快找出满足约束条件的一个解，或者是满足约束条件的解中找出某种意义下的最优解，通常用于解决离散值的最优化问题。

搜索方式不同

回溯法以深度优先的方式搜索解空间树。
分支限界法以广度优先或最小耗费优先的方式搜索解空间树。

对扩展结点的扩展方式不同

分支限界法中，每一个活结点只有一次机会成为扩展结点。
活结点一旦成为扩展结点，就一次性产生其所有儿子结点。

存储空间的要求不同

分支限界法的存储空间比回溯法大得多。
因此当内存容量有限时，回溯法成功的可能性更大。

二者区别小节

回溯法空间效率高，分支限界法往往更快。
限界函数常基于问题的目标函数，适用于求解最优化问题

分支限界法的基本思想：以广度优先或最小耗费（最大收益）优先的方式搜索解空间树。

分支限界法中，每一个活结点只有一次机会成为扩展结点。
活结点一旦成为扩展结点，就一次性产生其所有儿子结点。
其中导致不可行解或导致非最优解的儿子结点被舍弃。
其余儿子结点被加入活结点表PT中
含义：根据限界函数估算目标函数达到可能取值
选取可能使目标函数取得极值的结点优先进行搜索。
然后从活结点表中取下一结点成为当前扩展结点
重复上述过程：直至找到所需的解或活结点表为空时为止。

求解步骤

每个活结点仅有一次机会变成扩展结点
由扩展结点生成一步可达的新结点
在新结点中，删除不可能导出最优解的结点（限界策略）
将剩余的新结点加入活动表（队列）中
从活动表中选择结点再扩展（分支策略）
直至活动表为空

队列分支限界法

按照队列先进先出（FIFO）原则选取下一个结点为扩展结点
从活结点表中取出结点的顺序与加入结点的顺序相同
因此活结点表的性质与队列相同

优先队列分支限界法（代价最小或效益最大）

每个结点都有一个对应的耗费或收益，以此决定结点的优先级。
从优先队列中选取优先级最高的结点成为当前扩展结点
如果查找一个具有最小耗费的解，则活动表用小顶堆来建立，下一个扩展结点就是具有最小耗费的活结点。
如果希望搜索一个具有最大收益的解，则可用大顶堆来构造活结点表，下一个扩展结点是具有最大收益的活结点。

0/1背包问题

回溯求解0/1背包问题，虽剪枝减少了搜索空间，但整个搜索按深度优先机械进行，是盲目搜索（不可预测本结点以下的结点进行的如何）。

分支限界法首先确定一个合理的限界函数，并根据限界函数确定目标函数的界[down,up]
然后按照广度优先策略遍历问题的解空间树，在某一分支上，依次搜索该结点的所有孩子结点，分别估算这些孩子结点的目标函数的可能取值（对最小化问题，估算结点的down，对最大化问题，估算结点的up）。
如果某孩子结点的目标函数值超出目标函数的界，则将其丢弃，否则加入活动表等待处理。

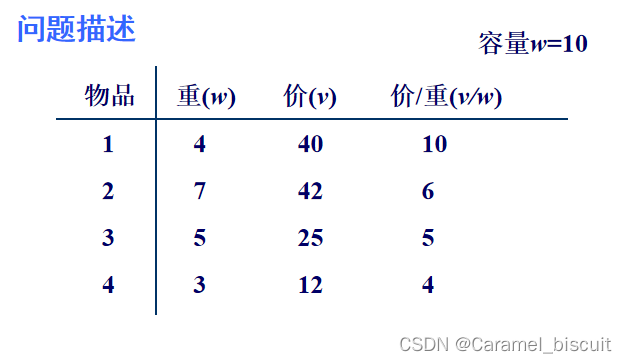
问题的解可表示为n元向量{x1, x2, … xn }, xi{0,1}，则可用子集树表示解空间, 在树中做广度优先搜索。
下界Vdb = 40(1,0,0,0)——贪心思想
上界Vub = 100
限界函数

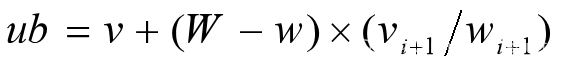
0-1背包步骤

首先，要对输入数据进行预处理，将各物品依其单位重量价值从大到小进行排列。
结点的优先级由已装袋的物品价值加上剩下的最大单位重量价值的物品装满剩余容量的价值和。
算法首先检查当前扩展结点的左儿子结点的可行性。如果该左儿子结点是可行结点，则将它加入到子集树和活结点优先队列中。
当前扩展结点的右儿子结点一定是可行结点，仅当右儿子结点满足上界约束时才将它加入子集树和活结点优先队列。
当扩展到叶结点时为问题的最优值。

int bound(){
	while(i<=n && w[i]<=cleft){
		cleft -= w[i];
		b += v[i];
		i++;
	}
	if(i<=n){
		b = b+(v[i]/w[i])*cleft;
		return b;
	}
}

while(i!=n+1){
	//检查当前扩展结点的左儿子结点
	int wt = cw + w[i];
	if(wt <= c){
		if(cv+v[i] > bestv){
			bestv = cv+v[i];
		}
		AddLiveNode(ub,cv+v[i],cw+w[i],true,i+1);
	}
	ub = Bound(i+1);
	//检查当前扩展结点的右儿子结点
	if(ub>=bestv){
		AddLiveNode(up,cv,cw,false,i+1)
	}
	//取下一个扩展结点
}

从0/1背包问题的搜索过程可看出：与回溯法相比，分支限界法根据限界函数不断调整搜索方向，选择最可能得到最优解的子树优先进行搜索->找到问题的解。

分支限界法的一般过程：

根据限界函数确定目标函数的界[down,up]
将待处理结点表PT初始化为空
对根节点的每个孩子结点x执行下列操作：估算结点x的目标函数值value，如果value>=down，则将x加入表PT中。
循环直到某个叶子结点的目标函数值在表PT中最大
i=表PT中值最大的结点
对结点i的每个孩子结点x执行下列操作：估算结点x的目标函数值value；若value≥down，则将结点x加入表PT中，若(结点x是叶子结点且结点x的value值在表PT中最大)，则将结点x对应的解输出，算法结束；若(结点x是叶子结点但结点x的value值在表PT中不是最大)，则令down=value，并且将表PT中所有小于value的结点删除；

单源路径问题

在有向图G中，每一边都有一个非负边权。要求图G的从源顶点s到目标顶点t之间的最短路径。
采用优先队列式分支限界，并用极小堆来存储活结点表，其优先级是结点所对应的当前路长。

解向量：X=(s, x2, …, t )，s 和t 分别为起点和终点
显示约束：xi=A, B, … (i=2, …, n)
隐式：cij≠∞
目标函数：cost(i )=min {cij +cost (j )} (i≤j≤n且顶点 j 是 i 的邻接点)
下界：把每一段最小的代价相加，2+4+5+3=14
上界：2+6+6+3=17 (s→B→E→H→t)

while(true){
	for(int j=1; j<=n; j++){
	// 顶点i和j间有边，且此路径长小于原先从源点到j的路径长
		if((c[E.i][j]<inf)&&(E.length+c[E.i][j]<dist[j])){
			//顶点i到j可达，且满足控制约束
			dist[j] = E.length+c[E.i][j];
			prev[j] = E.i;
			MinHeadpNode<Type> N;
			N.i=j;
			N.length=dist[j];
			H.insert(N);
		}
		try(H.DeleteMin(E));
		catch (OutOfBounds) {break;}  // 优先队列空
	}
}

装载问题

装载问题的队列式分支限界法仅求出所要求的最优值，稍后将进一步构造最优解。
在while循环中，首先检测当前扩展结点的左儿子结点是否为可行结点。如果是，则将其加入到活结点队列Q中。
然后，将其右儿子结点加入到活结点队列中(右儿子结点一定是可行结点)。2个儿子结点都产生后，当前扩展结点被舍弃。
活结点队列中，队首元素被取出作为当前扩展结点。
队列中每一层结点之后，都有一个尾部标记-1。
在取队首元素时，活结点队列一定不空。
当取出的元素是-1时，再判断当前队列是否为空。
如果队列非空，则将尾部标记-1加入活结点队列，算法开始处理下一层的活结点。
采用最大优先队列存储活结点表。活结点x在优先队列中的优先级定义为：从根结点到结点x的路径所相应的载重量Ew + 剩余集装箱的重量r。
子集树中叶结点所相应的载重量与其优先级相同，一旦有一个叶结点成为当前扩展结点，则可以断言该叶结点所相应的解即为最优解。此时可终止算法。

算法的改进

节点的左子树表示将此集装箱装船，右子树表示不将此集装箱装船。
设bestw是当前最优解；ew是当前扩展结点所相应的重量；r是剩余集装箱的重量。
当ew+rbestw时，可将其右子树剪去。此时若要船装最多集装箱，就应该把此箱装上船。
法MaxLoading初始时bestw=0，直到搜索到第一个叶结点才更新bestw。在搜索到第一个叶结点前，总有Ew+r>bestw, 此时右子树测试不起作用。
为确保右子树成功剪枝，应该在算法每一次进入左子树的时候更新bestw的值。