一、卡方检验
假设检验的一种,以实际观测值与期望值之间的偏离程度,解决是服从某个构成比率和是否具有相关性的问题。其偏离程度决定卡方值的大小,卡方值越小,偏差越小,实际值越趋于符合期望值。
二、步骤
在显著性为α=0.05下,检验职业和是否发生感冒是否独立性
假设检验
原假设:H0一般是我们想要拒绝的假设,一般是=、>=、<=。
备选假设:H1是我们想要接受的假设,一般是<> 、 >、<
①原假设职业和是否发生感冒是相互独立的,没有相关性。
②备选假设职业和是否发生感冒是有相关性,也就是所处职业和感冒有相关。
职业与是否发生感冒 | ||||
| 程序员 | 教师 | 园艺师 | 合计 |
发生感冒 | 58 | 52 | 63 | 173 |
未发生感冒 | 42 | 41 | 44 | 127 |
合计 | 100 | 93 | 107 | 300 |
计算期望值
期望值=行合计*列合计/总计。
职业与是否发生感冒 | ||||
| 程序员 | 教师 | 园艺师 | 合计 |
发生感冒 | 100 * 173 /300 =57.67 | 93 * 173 /300 =53.63 | 107 * 173 / 300 =61.7 | 173 |
未发生感冒 | 100 * 127 /100 =42.33 | 93 * 127 /100 =39.37 | 107 * 127 /100 =42.3 | 127 |
合计 | 100 | 93 | 107 | 300 |
计算卡方值
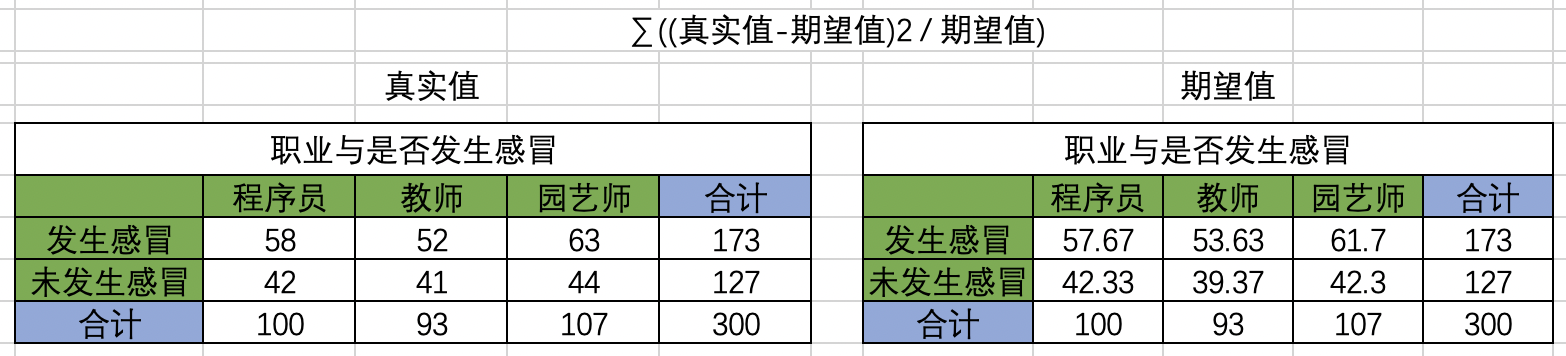
卡方值 =(真实值-期望值)的平方 / 期望值。
卡方值相加,得到最终卡方值。卡方=0.1859
计算卡方自由度
卡方自由度:Df=(a-1)* (b-1); a 和 b 分别为检验条件的分类数。
例:Df = (2-1)* (3-1)=1*2=2
一般选显著性水平为0.05,自由度为2,取2与0.05的交叉点为5.991.
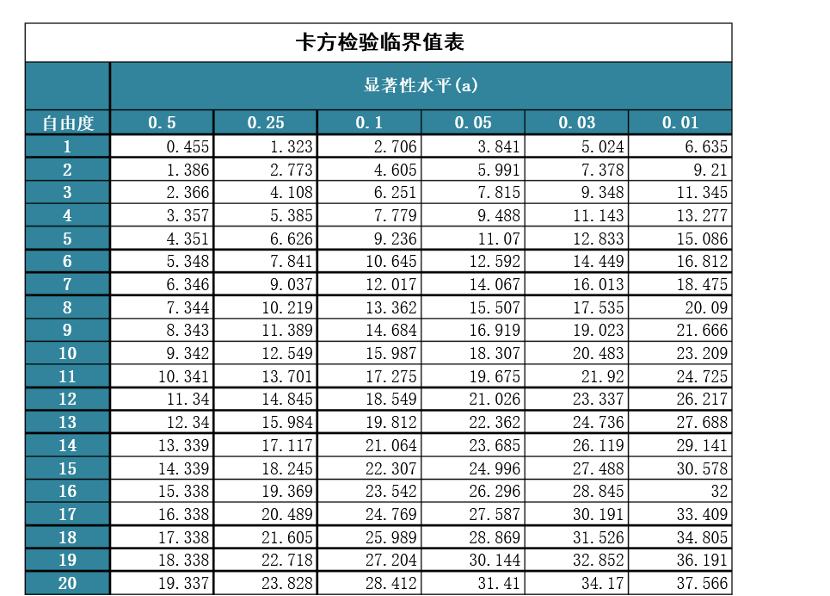
卡方=0.1859 < 5.991,卡方值在临界值内,可以判断得到无法拒绝原假设,那就是接受。职业和感冒相互之间没有影响。
python实现

p值大于0.05,不存在显著性差异,认为职业和感冒独立。
卡方的限制条件
①R*C表卡方检验(例子所示):
理论数不能有小于1的,<5的格子不能超过20%,就是每个类别的频数不能小于1,然后小于5的类别数要大于20%。
②2*2列联表