时间复杂度

• 时间复杂度是用来估算算法运行时间的式子（单位）；

• 一般来说，时间复杂度高的算法比时间复杂度低的算法慢；

• 常见的时间复杂度（按照算法运行所耗的时间排序）

O(1) < O(logn) < O(n) < O(nlogn) < O(n^2^) < O (n^2^logn) < O(n^3^)

---

时间复杂度为：O(1) 算法枚举的执行一次或几次

例子1 输出一句
printf("Hello World\n");

例子2 输出三句时间复杂度也是O(1)
printf("Hello jim\n");
printf("Hello jack\n");
printf("Hello kevin\n");

---

时间复杂度为：O(logn) 算法每次执行都折半，那么该算法循环的次数为以2为底n的对数，即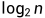，那么该算法的时间复杂度为O(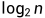)或写成O(logn)

例子1
int n = 64;
while (n > 1)
{
    n /= 2;
    printf("n = %d\n", n);
}

---

时间复杂度为：O(n) 算法循环的执行n次

例子1
int n = 100;
for (int i = 0; i < n; i++)
    printf("i = %d\n", i);

---

时间复杂度为：O(nlogn) 算法循环的执行n次，并每次嵌套内循环，这个内循环每次执行都折半

例子1
int n = 64;
for (int i = 0; i < n; i++)
{
    int temp = n;
    while (temp > 1)
    {
        temp /= 2;
        printf("temp = %d\n", temp);
    }
}

---

时间复杂度为：O(n^2^) 算法循环执行n次，并每次嵌套内循环，这个内循环每次执行n次

例子1
for (int i = 0; i < n; i++)
{
    printf("i = %d\n", i);
    for (int j = 0; j < n; j++)
        printf("j = %d\n", j); 
}

---

时间复杂度为：O(n^2^logn) 算法循环执行n次，并每次嵌套内循环，这个内循环每次执行n次,并这个内循环再嵌套一个内循环，并且这个内循环每次执行折半

例子1
int k = 64;
for (int i = 0; i < n; i++)
{
    printf("i = %d\n", i);
    for (int j = 0; j < n; j++)
    {
        printf("j = %d\n", j);
        int temp = k;
        while (temp > 1)
            temp /= 2;
    } 
}

---

时间复杂度为：O(n^2^logn) 算法循环执行n次，并每次嵌套内循环，这个内循环每次执行n次,并这个内循环再嵌套一个内循环，并且这个内循环每次执行n次

例子1
for (int i = 0; i < n; i++)
{
    printf("i = %d\n", i);
    for (int j = 0; j < n; j++)
    {
        printf("j = %d\n", j);
        for (int k = 0; k < n; k++)
            printf("k = %d\n", k);
    } 
}

---

空间复杂度

• 空间复杂度是用来估算算法内存占用大小的式子（单位）；

• 空间复杂度的表示方式跟时间复杂度完全一样

1. 算法使用了一个或几个变量，空间复杂度为：O(1)

2. 算法使用了长度为n的一维列表，空间复杂度为：O(n)

3. 算法使用了长度为m行n列的二维列表，空间复杂度为：O(mn)

4. 算法使用了j个长度为m行n列的二维列表，空间复杂度为：O(jmn)

5. 算法使用了i个三维列表，并每个三维列表有j个长度为m行n列的二维列表，空间复杂度为：O(ijmn)

---

空间复杂度为：O(1)

例子1 该算法只在栈中开辟了n这3个变量，所以空间复杂度为O(1)
int n = 1;

例子2 该算法只在栈中开辟了m，n，k这3个变量，所以空间复杂度为O(1)
int m = 1;
int n = 1;
int k = 1;

例子3 该算法只在栈中开辟了i，j，temp这3个变量，所以空间复杂度为O(1)
void sort_arr(int *const arr, const int n)
{
    for (int i = 0; i < n; i++)
    {
        for (int j = i + 1; j < n; j++)
        {
            if (arr[i] > arr[j])
            {
                int temp = arr[i];
                arr[i] = arr[j];
                arr[j] = temp;
            }
        }
    }
}

---

ending😃