电子技术——AB类输出阶

原理
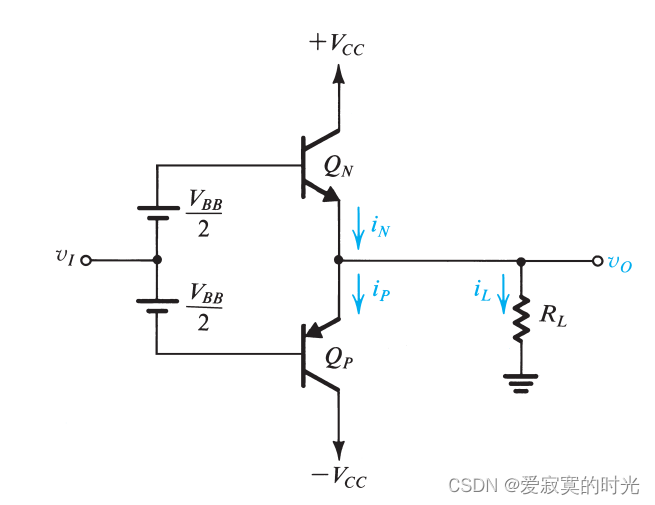
交越失真可以通过通过一个较小的偏置电流解除,如下图:
Q
N
Q_N
QN 和
Q
P
Q_P
QP 的基极之间存在偏置电压
V
B
B
V_{BB}
VBB 。对于完美匹配的晶体管,当
v
I
=
0
v_I = 0
vI=0 的时候,此时
v
O
=
0
v_O = 0
vO=0 。每一个晶体管都存在偏置电流:
i N = i P = I Q = I S e V B B / 2 V T i_N = i_P = I_Q = I_S e^{V_{BB}/2V_T} iN=iP=IQ=ISeVBB/2VT
静态偏置电流由电压 V B B V_{BB} VBB 产生。
当 v I v_I vI 正向增大的时候,此时输出电压为:
v O = v I + V B B 2 − v B E N v_O = v_I + \frac{V_{BB}}{2} - v_{BEN} vO=vI+2VBB−vBEN
若设置偏置电压 V B B 2 = v B E N \frac{V_{BB}}{2} = v_{BEN} 2VBB=vBEN ,那么发射极将完美跟随基极电压。
此时会有 i L i_L iL 的电流通过负载,有:
i N = i P + i L i_N = i_P + i_L iN=iP+iL
由于 i N i_N iN 的增大会引起 v B E N v_{BEN} vBEN 的增大,这会导致跟随偏移。然而我们知道环路电压不变,即:
v B E N + v E B P = V B B v_{BEN} + v_{EBP} = V_{BB} vBEN+vEBP=VBB
说明 v B E N v_{BEN} vBEN 增大会引起 v E B P v_{EBP} vEBP 减小,最终导致 i P i_P iP 减小。更具体的:
V T ln i N I S + V T ln i P I S = 2 V T ln I Q I S V_T\ln{\frac{i_N}{I_S}} + V_T\ln{\frac{i_P}{I_S}} = 2V_T\ln{\frac{I_Q}{I_S}} VTlnISiN+VTlnISiP=2VTlnISIQ
这导出:
i N i P = I Q 2 i_Ni_P = I_Q^2 iNiP=IQ2
联立导出 i N i_N iN 和 i L i_L iL 的关系:
i N 2 − i L i N − I Q 2 = 0 i_N^2 - i_Li_N - I_Q^2 = 0 iN2−iLiN−IQ2=0
根据上述的推导,我们发现在信号正半周期的时候,此时负载电流由 Q N Q_N QN 提供,作为射极电压跟随器。同时 Q P Q_P QP 的导通电流将随着 v O v_O vO 的增大而减小,对于较大的 v O v_O vO 此时 Q P Q_P QP 的导通电流可以忽略不计。
同理对于负半周期,此时负载电流由 Q P Q_P QP 提供,作为射极电压跟随器。同时 Q N Q_N QN 的导通电流将随着 v O v_O vO 的增大而减小,对于较大的 v O v_O vO 此时 Q N Q_N QN 的导通电流可以忽略不计。
我们得出结论,AB类输出阶的行为和B类输出阶的行为大致相似。其中有一点不同,对于较小的 v I v_I vI 两个晶体管均导通,当 v I v_I vI 增大或者减小两个晶体管都工作在导通区域,因为两个晶体管是平滑过渡,因此不存在交越失真。下图展示了AB类输出阶的传导曲线:

AB类输出阶的功率推导和B类大致相似。唯一的区别是在静态点的时候,此时每一个晶体管都存在静态耗散功率
V
C
C
I
Q
V_{CC}I_Q
VCCIQ 。因为
I
Q
I_Q
IQ 非常小,远小于最大负载电流,因此静态耗散功率基本上很小。特别的,我们可以将静态耗散功率加到最大耗散功率上,来计算最大安全功率。
输出阻抗
若我们假设信号源 v I v_I vI 是理想的,则AB类输出阶的输出阻抗可以由下图决定:
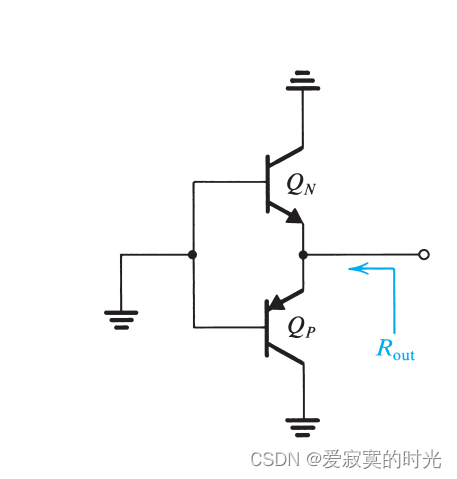
输出阻抗为:
R o u t = r e N ∣ ∣ r e P R_{out} = r_{eN} || r_{eP} Rout=reN∣∣reP
这里 r e N r_{eN} reN 和 r e P r_{eP} reP 是小信号模型下 Q N Q_N QN 和 Q P Q_P QP 的射极电阻。对于给定的电流,有:
r e N = V T i N r_{eN} = \frac{V_T}{i_N} reN=iNVT
r e P = V T i P r_{eP} = \frac{V_T}{i_P} reP=iPVT
也就是:
R o u t = V T i N ∣ ∣ V T i P = V T i N + i P R_{out} = \frac{V_T}{i_N} || \frac{V_T}{i_P} = \frac{V_T}{i_N + i_P} Rout=iNVT∣∣iPVT=iN+iPVT
因为当 i N i_N iN 增大的时候 i P i_P iP 减小,反之亦然,输出阻抗可以近似的看成是一个固定的值和 v I = 0 v_I = 0 vI=0 的静态点相同。在较大的输出电流的情况下,此时 i N i_N iN 或者是 i P i_P iP 占主导,此时 R o u t R_{out} Rout 降低。


![[工具笔记]1.UnityEngine.Plane](https://img-blog.csdnimg.cn/b758ee6e89114386babc0962ed77e73e.png)




![[4.10]-AutoSAR零基础学习-Secure Debug(SHE+)(一)](https://img-blog.csdnimg.cn/54254c973ba845cc801cf62359fddc3f.png)