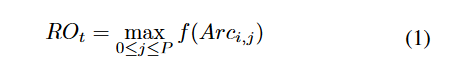Reinforcement-Learning-Based Evolutionary Algorithm Using Solution Space Clustering For Multimodal Optimization Problems
基于强化学习的多模态优化问题解空间聚类进化算法
摘要
在进化算法中，如何有效地选择用于生成后代的交互式解决方案是一个具有挑战性的问题。尽管提出了许多算子，但大多数算子随机选择交互式解（父解），对各种问题中的景观特征没有特殊性。
为了解决这一问题，本文提出了一种基于强化学习的进化算法，以在近似吸引池内选择解。
在该算法中，解空间由k维树划分，子空间的特征从两个方面进行近似：目标值和不确定性。
因此，构建了两个强化学习（RL）系统来确定搜索位置：基于目标的RL利用吸引盆地（聚集子空间），
而基于不确定性的RL探索搜索相对较少的子空间。在广泛使用的基准函数上进行了实验，证明该算法优于其他三种流行的多模态优化算法。

介绍
许多实际问题具有局部最优或多重全局最优，例如电磁设计、蛋白质结构设计和特拉斯结构优化[1]，其中多个有前景的解决方案可以带来显著的好处。因此，优化器应该避免陷入局部优化，并找到更多的备选优化。这是一个具有挑战性的要求，特别是对于传统的数学优化算法。
analysis of the landscape
进化算法（EA），如遗传算法（GA）[2]、粒子群优化（PSO）[3]、差分进化（DE）[4]和蚁群优化（ACO）[5]，使用基于种群的范式同时进行搜索。
群体中的所有解决方案都可以与其他解决方案交互，并使用不同的操作员生成新的解决方案，这些算子的选择。对算法的效率有影响。
例如，PSO中不同的速度更新方程将导致不同的优化结果，类似地，不同的变异算子（如rand/1、best/1和rand/2）将生成不同的新解。
然而，大多数算法随机选择交互式解决方案（父母），不考虑不同的问题。尽管一些算法针对不同的搜索策略合并了多个进化算子，但如何构造算子集以及如何自适应地选择算子成为新的挑战性问题。
从另一个角度来看，一些作品侧重于景观分析，然后解决方案可以根据其所在的景点盆地进行合作。？？？？

EA中最常用的峰值检测方法是基于人群的聚类技术[6]-[8]。根据个体的适合度值和位置，总种群可以分为几个亚种群。在每个亚群中，个体可以被视为在同一个峰值进行搜索。但由于种群规模稳定，这些算法往往具有有限的数据，并且很难通过聚类方法保证峰值检测的精度。此外，由于个体的适应值和位置不断变化，聚类只能反映当前的人口分布，而不能反映问题景观的确切特征。
为了克服上述问题，本文引入了一种基于强化学习（RL）的进化算法，该算法采用了解空间聚类（RLEA-SSC）技术，其中所有生成的解都用于估计吸引盆地并指导父母的选择（交互式解）。这里的吸引池包含局部最优点周围的所有点，当使用贪婪的局部搜索时，这些点可以导致最优点。
In the algorithm, the k−dimensional tree (kd-tree) is applied to discretize the solution space, hence subspaces can serve as the units of clustering and they can be clustered via the RL-learned potential values to approximate the basin of attraction.
该算法采用k维树(kd-树)对解空间进行离散化，将子空间作为聚类的单位，通过rl学习势值对子空间进行聚类，逼近吸引池。
同时，为了跟踪更多的吸引盆地，分别构建了两个RL系统来开发和探索子空间。实验结果还证明了与其他最先进的多模态优化算法相比的竞争性能。
本文的其余部分组织如下：第二节描述了基于聚类的多模态优化算法和基于RL的EA的相关工作。第三节介绍了RLEA-SSC的详细信息，第四节给出了实验分析。最后，第五节总结了论文，第六节包括确认。

RELATED WORK 相关工作
对于一个算法来说，定位多个最优值是一个挑战。在现有的多模态优化算法中，提出了许多小生境方法来跟踪有希望的最优值。一些改进的DE算法基于拥挤比或距离构建邻域[9]，以保持种群覆盖不同的峰值。一些PSO变体[10]定义拓扑以限制粒子之间的相互作用。然而，小生境技术对小生境参数敏感，基于邻域的算法总是随机选择拓扑。如果没有适当的参数设置，算法的性能将显著下降。如何设计一种覆盖所有潜在优化的有效方法仍然是一项具有挑战性的任务。在过去的十年中，一些算法试图在搜索过程中自动近似地形。
如上所述，大多数具有景观近似的算法都基于种群的聚类。该问题的景观模型是根据人口的当前分布及其个体的适应值建立的，因此用于描述问题特征的信息有限。此外，人口的分布是动态变化的，具有很大的随机性。这些复杂的情况对聚类的精度提出了更高的要求。

利用最近更好的聚类技术，提出了一种小生境协方差矩阵自适应进化策略（CMA-ES）[6]，其中构建了个体的生成树，并将树切成簇，以便在不同的预测盆地中保持CMA-ES。在没有预定义参数的情况下，应用亲和力传播聚类来自动预测景观轮廓[7]，其中聚类方法有助于定位多个峰值，而无需额外的适应度评估。在[11]中，将多模态优化问题转化为多目标优化问题，其中多个优化可以成为帕累托最优解，并且更容易同时定位。类似地，[12]中提出了多模态优化算法（EMO-MMO）的进化多目标优化。在EMO-MMO中，使用多目标优化算法来近似景观，并通过切割采样点的景观来检测潜在的峰值。

Previous algorithms tend to use the current population as clustering data or use many pre-samplings to model the landscape: the former mechanism is inclined to miss some valuable historical information and the latter one will require many fitness evaluations.
以往的算法倾向于使用当前种群作为聚类数据或使用大量的预采样来建模景观，前者容易遗漏一些有价值的历史信息，而后者则需要进行多次适应度评估。
幸运的是，在对问题进行建模时，可以应用许多机器学习算法。同时，EA参与了关于如何选择有前景的空间进行搜索的决策序列，RL可以是优化选择和逼近每个决策潜力的代表性方法。然而，当前关于RL在EA中的应用的大多数工作都集中在参数控制和算子选择上，而不是本文所关注的潜在空间的选取。
RL用于控制步长[13]和突变（重组）比率[14]，其中子代的改善比率被设置为奖励，那么累积奖励（行动值）可以用作参数设置有多好的指标。与特定参数控制相比，通用参数控制器可以同步控制各种参数。使用定义的状态向量，包括表型和基因型的多样性、适应度值的均值和方差以及停滞计数器[15]，用树动态划分状态空间，并使用时间差法更新动作值。因此，可以选择参数集。除了参数控制之外，RL还用于控制操作员的选择。作为四个变异和交叉算子的混合，在搜索过程中应用了三种RL更新算法来选择算子，提高了搜索效率[16]。遵循同样的想法，进化规划[17]选择了四个具有自适应比率的变异算子（高斯、列维、柯西和单点变异算子），这些算子根据行动值设置，并以后代的适应值作为奖励。
尽管RL系统被引入到EA的框架中，但RL组件的设计与问题有关，如何构建动作集也成为一个挑战。最重要的是，几乎所有的奖励都是根据其后代的健康值或提高的可能性来设置的，因此，行动的选择范围很快就会收敛到一个小范围。由于缺乏足够的探索，即使是有希望获得长期回报的行动也可能无法选择。
RLEA-SSC
在本节中，将详细介绍RLEA-SSC，包括RLEA-SC框架、RL组件、子空间聚类、动作选择以及与EA的集成。
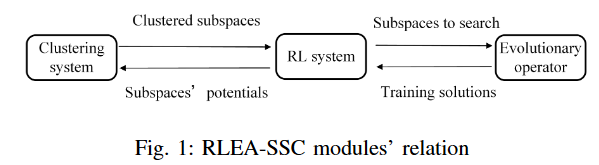
在RLEA-SSC中，为了描述连续解空间，用k-d树划分空间。建立了两个RL系统，从两个角度近似子空间的搜索潜力：目标值和不确定性。因此，RL引导进化算子在具有相应档案的选定子空间中生成新的解。此外，子空间被聚类以近似吸引盆地，算法中的模块关系如图1所示。

RL前期工作
强化学习是学习在特定情况下应该做什么，以最大化数字奖励信号。状态用于反映当前的情况，并且该行为可以从外部获得奖励（在RL中称为环境）。对于学习者（在RL中称为代理）来说，目标是通过试错行为最大化累积奖励。RL的过程如图所示。2[18]。在时间t，代理采取行动At，环境将向代理返回奖励Rt。同时，代理的状态从St转换为St+1。最后，可以使用更新的策略重复该过程的其余部分。

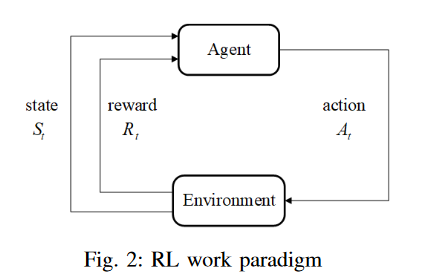
在接下来的部分中，构建了两个RL框架：基于目标的RL和基于不确定性的RL。两者都有相同的状态定义，但动作集和奖励设置不同。其中一个RL系统用目标值评估子空间，并决定要搜索哪些聚类子空间；另一种方法评估每个子空间的搜索不确定性，并指导在搜索相对较少的子空间中进行搜索。
1） 状态定义：对于EA，最终目标是将个体收敛到具有最高适应值的点。当算法使用历史解作为父代来产生后代时，历史解的分布可以反映算法的搜索状态。在RLEA-SSC中，算法本身可以被视为代理，历史解的分布被定义为代理的状态。当解空间由k-d树[19]划分时，k-d树可以查询位置属于哪个子空间。此外，为了简化状态的复杂性，每个子空间都使用一个存档来存储特定的历史解。因此，存档可以反映子空间中的搜索历史。以二维解空间为例：搜索空间可以划分为M个矩形子空间，第i个子空间Subi将分配一个解档案Arci（稍后介绍）。时间t的状态可以表示为St=（Arc1（t），Arc2（t）…，ArcM（t））。
2） 行动定义：在哪里搜索是决定优化算法效率和准确性的决定性选择。解的目标值直接决定优化结果。考虑到这一点，设计了一种根据客观值反馈进行搜索的行动。然而，对于一个复杂的问题，基于客观反馈的估计可能并不精确，尤其是在缺乏足够的历史信息的情况下。因此，还设计了另一种基于搜索不确定性的动作。在RLEA-SSC中，这两种类型的操作选择子空间，其中相应的归档解决方案可以作为父级来生成新的解决方案。此外，基于目标的行动通过目标值更新行动值，而基于不确定性的行动通过不确定性更新行动值。
基于目标的行动去，选择集群。集群中的所有元素都是k-d树分区的子空间，其存档将合并为存档以生成新的解决方案。对于每个簇，它可以被识别为一个吸引盆地，其中子空间被近似为一个有希望的峰值区域。例如，如果五个子空间被聚类为：Go1＝（Sub1，Sub2，Sub3），Go2＝（Sub4，Sub5），并且基于目标的动作集Ao被表示为：Ao＝（Go1，Go2）。类似地，基于不确定性的动作选择集群。稍有不同的是，将从集群中选择一个子空间，其存档将用于生成新的解决方案。基于不确定性的簇和动作集分别表示为Gu和Au。
3） 奖励设置：对于RL系统，累积奖励的最大化是代理的目标，奖励的设计将直接决定算法的搜索偏好。为了权衡在具有高目标价值的子空间中的开发与对有前景的吸引盆地的探索，RLEA-SSC结合了两种类型的奖励：基于目标的奖励和基于不确定性的奖励。当采取动作At时，生成属于子空间簇Gi的新解Sol。对于最大化优化问题，基于目标的奖励ROt计算如下等式（1）：