Datawhale统计学习方法打卡Task05

news2024/9/25 15:22:20

学习教材《统计学习方法（第二版）》李航

学习内容：第5章决策树

第五章决策树

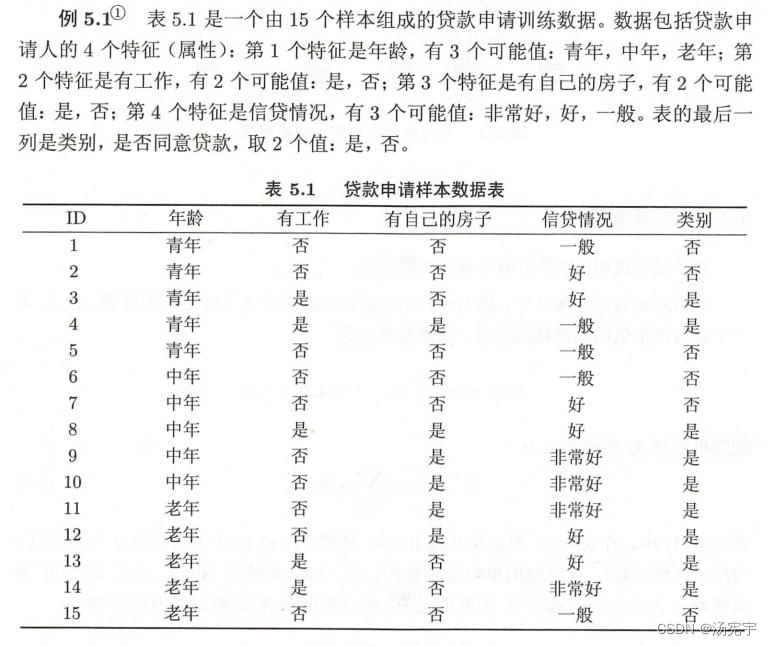
决策树是一种基本你的分类与回归方法。决策树模型呈树形结构，在分类问题中，表示基于特征对实例进行分类的过程。通过ID3和C4.5介绍特征的选择、决策树的生成以及决策树的修剪，最后介绍CART算法。

5.1决策树模型与学习

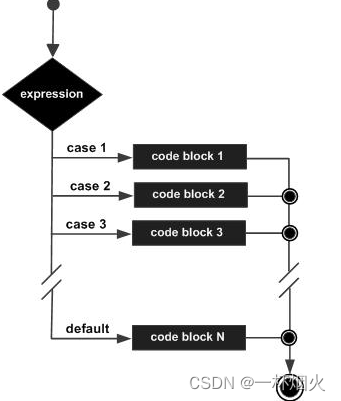
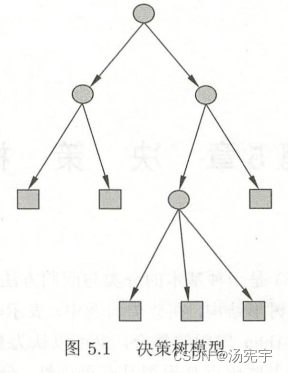
定义5.1 （决策树）分类决策树模型是一种描述对实例进行分类的树形结构。决策树由节点（node）和有向边（directed edge）组成。结点有两种类型：内部结点和叶节点。内部结点表示一个特征或属性，叶节点表示一个类。

用决策树分类，从根节点开始，对实例的某一特征进行测试，根据测试结果，将实例分配到子节点；这是每一个子节点对应着该特征的一个取值。如此递归的对顺利进行测试并分配，指导达到叶节点。最后将实例分到叶节点的类中。

5.1.2决策树与if-then规则

由决策树的根节点到叶节点的每一条路径构建一条规则；路径上内部结点对应着规则的条件，二叶节点的类对应着规则的结论。互斥并且完备。

5.1.3决策树与条件概率分布

5.1.4决策树学习

决策树学习算法包含特征选择、决策树的生成与决策树的剪枝。

决策树学习的算法有ID3、C4.5与CART。

5.2特征选择

5.2.1特征选择问题

（1）计算初始信息熵

根据信息增益的方法，计算

$H(D)=-\frac{9}{15}\log_2\frac{9}{15}-\frac{6}{15}\log_2\frac{6}{15}=0.971$

然后计算各特征对数据集D的信息增益。分别以 $A_1,A_2,A_3,A_4$ 表示年龄、有工作、有房子和信贷情况4个特征，

（2）计算每个特征的信息增益

对于A1的信息增益

$\begin{aligned} H(D|A_1)&=\sum_{i=1}^n\frac{|D_i|}{|D|}H(D_i)\\ &=-\frac{5}{15}H(D_1)-\frac{5}{15}H(D_2)-\frac{5}{15}H(D_3)\\ &=-\frac{5}{15} (-\frac{2}{5}\log_2\frac{2}{5}-\frac{3}{5}\log_2\frac{3}{5})-\frac{5}{15} (-\frac{3}{5}\log_2\frac{3}{5}-\frac{2}{5}\log_2\frac{2}{5}) -\frac{5}{15} (-\frac{4}{5}\log_2\frac{4}{5}-\frac{1}{5}\log_2\frac{1}{5})\\ &=0.888 \end{aligned}$

则：

$g(D,A_1)=0.971-0.888=0.083$

对于A2的信息增益

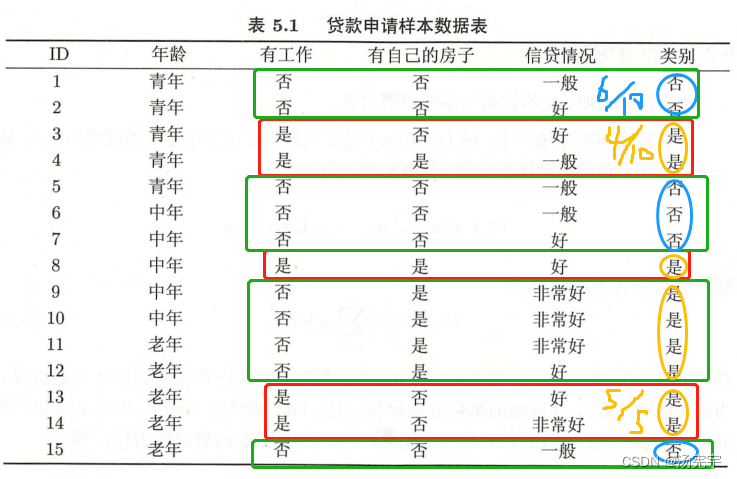
$\begin{aligned} g(D,A_2)&=H(D)-H(D|A_2)\\ &=0.971-\frac{5}{15}H(D_2)-\frac{10}{15}H(D_2)\\ &=0.971--\frac{5}{15}(-\frac{5}{5}\log_2\frac{5}{5}--\frac{0}{5}\log_2\frac{0}{5})-\frac{10}{15}(-\frac{4}{10}\log_2\frac{4}{10}-\frac{6}{10}\log_2\frac{6}{10})\\ &=0.324 \end{aligned}$

对于A3的信息增益：

$\begin{aligned} g(D,A_3)&=H(D)-H(D|A_3)\\ &=0.971-\frac{6}{15}H(D_3)-\frac{9}{15}H(D_3)\\ &=0.971-\frac{6}{15}(-\frac{6}{6}\log_2\frac{6}{6}--\frac{0}{6}\log_2\frac{0}{6})-\frac{9}{15}(-\frac{3}{9}\log_2\frac{3}{9}-\frac{6}{9}\log_2\frac{6}{9})\\ &=0.971-0.5509=0.4201 \end{aligned}$

对于A4的增益：

$g(D|A_4)=0.971-0.608=0.363$

5.2.3信息增益比

以信息增益作为划分训练数据集的特征，存在偏向于选择去质较多的特征的问题。使用信息增益比（information gain ratio）可以对这一问题进行校正。这是特征选择的另一准则。

$g_R(D|A)=\frac{g(D|A)}{H_A(D)}$

5.3 决策树的生成

5.3.1 ID3算法

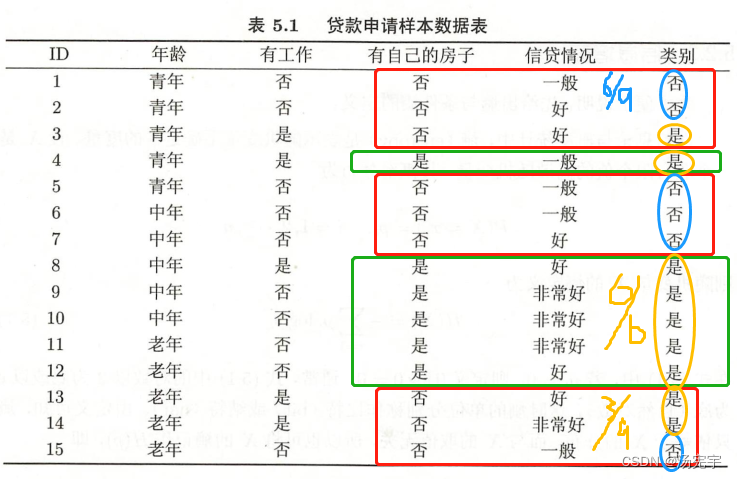
例5.3 对表5.1的训练数据集，利用ID3算法建立决策树

利用例5.2的结果，由于特征A3（有房子）的信息增益最大，所以选择特征A3作为根节点特征。他讲训练数据集D划分为两个子集D1（A3=是）和D2（A3=否）。由于D1只有同一类样本点（A3=是），所以他成为一个叶节点，节点标记为是。

对D2则需从A1（年龄）A2（有工作）和A4（信贷情况）中选择新的特征。计算各个特征的信息增益：

$g(D_2,A_1)=H(D_2)-H(D_2|A_1)=-\frac{3}{9}\log_2\frac{3}{9}-\frac{6}{9}\log_2\frac{6}{9}-[\frac{4}{9}(-\frac{1}{4}\log_2\frac{1}{4}-\frac{3}{4}\log_2\frac{3}{4})-\frac{2}{9}(0)-\frac{3}{9}(-\frac{2}{3}\log_2\frac{2}{3}-\frac{1}{3}\log_2\frac{1}{3})]=0.918-0.666=0.251$

$g(D_2,A_2)=H(D_2)-H(D_2|A_2)=0.918$

$g(D_2,A_4)=H(D_2)-H(D_2|A_4)=0.474$

选择信息增益最大的特征 $A_2$ （有工作）作为结点的特征。由于 $A_2$ 有两个可能取值，从这一节点引出两个子节点：一个对应“是”子节点，包含3个样本，他们属于同一类，所以这是一个叶节点，标记为“是”；另一个对应“否”（无工作）的子节点，包含6个样本，他们也属于同一类，所以这也是一个叶节点，类标记为“否”。这样生成决策树：

ID3算法只有树的生成，所以该算法生成的树容易产生过拟合。

5.3.2 C4.5的生成算法

C4.5算法与ID3算法类似，C4.5算法对ID3算法进行了改进，采用信息增益比来选择特征。

5.4 决策树的剪枝

5.5 CART算法

分类与回归树（classification and regression tree, CART）模型。以下将用于分类和回归的树统称为决策树。CART算法由以下两步组成：

（1）决策树生成：基于训练数据集生成决策树，生成的决策树要尽量大；

（2）决策树剪枝：用验证集对已生成的树进行剪枝并选择最优子树，这时用损失函数最小作为剪枝的标准。

5.5.1 CART生成

对回归树用平方误差最小化准则，对分类树用基尼指数（Gini index）最小化准则，进行特征选择，生成二叉树。

1.回归树的生成

假设X与Y分别为输入和输出变量，并且Y是连续变量，给定训练数据集

$D=\{(x_1,y_1),(x_2,y_2),\cdots,(x_N,y_N)\}$

考虑生成回归树。

2. 分类树的生成

例5.4 根据表5.1所给训练数据集，应用 CART算法生成决策树。

5.5.2 CART剪枝

习题

习题5.1

根据表5.1所给的训练数据集，利用信息增益比（C4.5算法）生成决策树

习题5.2

利用如表5.2所示训练数据，试用平方误差损失准则生成一个二叉回归树

习题5.3

证明CART剪枝算法中，当α确定时，存在唯一的最小子树 $T_\alpha$ 使损失函数 $C_\alpha(T)$ 最小。

习题5.4

证明CART剪枝算法中求出的子树序列 $\{T_0,T_1,\cdots,T_n\}$ 分别是区间 $\alpha\in[\alpha_i,\alpha_{i+1}]$ 的最优子树 $T_\alpha$ ,这里 $i=0,1,\cdots,n\;\;0=\alpha_0<\alpha_1<\cdots<\alpha_n<+\infty$