第三章 线性神经网络
代码:d2l-zh/pytorch/chapter_linear-networks
3.1 线性回归
3.1. 线性回归 — 动手学深度学习 2.0.0 documentation
解析解
线性回归的解可以用一个公式简单地表达出来,这类解叫作解析解(analytical solution)。
首先,我们将偏置b合并到参数w中,合并方法是在包含所有参数的矩阵中附加一列。我们的预测问题是最小化。
这在损失平面上只有一个临界点,这个临界点对应于整个区域的损失极小点。
将损失关于
∣
∣
y
−
X
w
∣
∣
2
||\bold y-\bold Xw||^2
∣∣y−Xw∣∣2的导数设为0,得到解析解:
w ∗ = ( X T X ) − 1 X T y \bold w^*=(\bold X^T \bold X)^{-1} \bold X^T \bold y w∗=(XTX)−1XTy
像线性回归这样的简单问题存在解析解,但并不是所有的问题都存在解析解。解析解可以进行很好的数学分析,但解析解对问题的限制很严格,导致它无法广泛应用在深度学习里。
随机梯度下降
算法的步骤如下: (1)初始化模型参数的值,如随机初始化; (2)从数据集中随机抽取小批量样本且在负梯度的方向上更新参数,并不断迭代这一步骤。
最优化方法一:梯度下降法_意念回复的博客-CSDN博客_梯度下降优化算法
矢量化加速
SIMD
在训练我们的模型时,我们经常希望能够同时处理整个小批量的样本。 为了实现这一点,需要我们对计算进行矢量化, 从而利用线性代数库,而不是在Python中编写开销高昂的for循环。
%matplotlib inline
import math
import time
import numpy as np
import torch
n = 10000
a = torch.ones([n])
b = torch.ones([n])
c = torch.zeros(n)
timer = Timer()
for i in range(n):
c[i] = a[i] + b[i]
f'{timer.stop():.5f} sec'
# '0.09661 sec'
timer.start()
d = a + b
f'{timer.stop():.5f} sec'
# '0.00021 sec'
结果很明显,第二种方法比第一种方法快得多。 矢量化代码通常会带来数量级的加速。 另外,我们将更多的数学运算放到库中,而无须自己编写那么多的计算,从而减少了出错的可能性。
3.2 线性回归的从零开始实验
3.2. 线性回归的从零开始实现 — 动手学深度学习 2.0.0 documentation
课后题
如果我们将权重初始化为零,会发生什么。算法仍然有效吗?
谈谈神经网络权重为什么不能初始化为0
在单层网络中(一层线性回归层),将权重初始化为零时可以的,但是网络层数加深后,在全连接的情况下,在反向传播的时候,由于权重的对称性会导致出现隐藏神经元的对称性,使得多个隐藏神经元的作用就如同1个神经元,算法还是有效的,但是效果不大好。
3.3 线性回归的简洁实现
3.3. 线性回归的简洁实现 — 动手学深度学习 2.0.0 documentation
为什么机器学习优化算法都采取梯度下降(一阶导算法),而不采用牛顿法(二阶导算法),收敛速度更快,一般能算出一阶导, 二阶导也应该能算。
为什么机器学习中通常使用梯度下降进行训练
高阶导数信息的准确估计需要训练数据的批量更大
复杂高维神经网络的代价函数具有极多鞍点使高阶方法失效
其实核心还是神经网络参数数量大造成高阶方法计算、存储成本难以接受
如果样本大小不是批量数的整数倍,那需要随机剔除多余的样本吗?
如果是100个样本且batchsize=60 :
(1)就取剩下的40个(2)丢掉剩下的40个(3)从下一个epoch再补20个
3.4 softmax回归
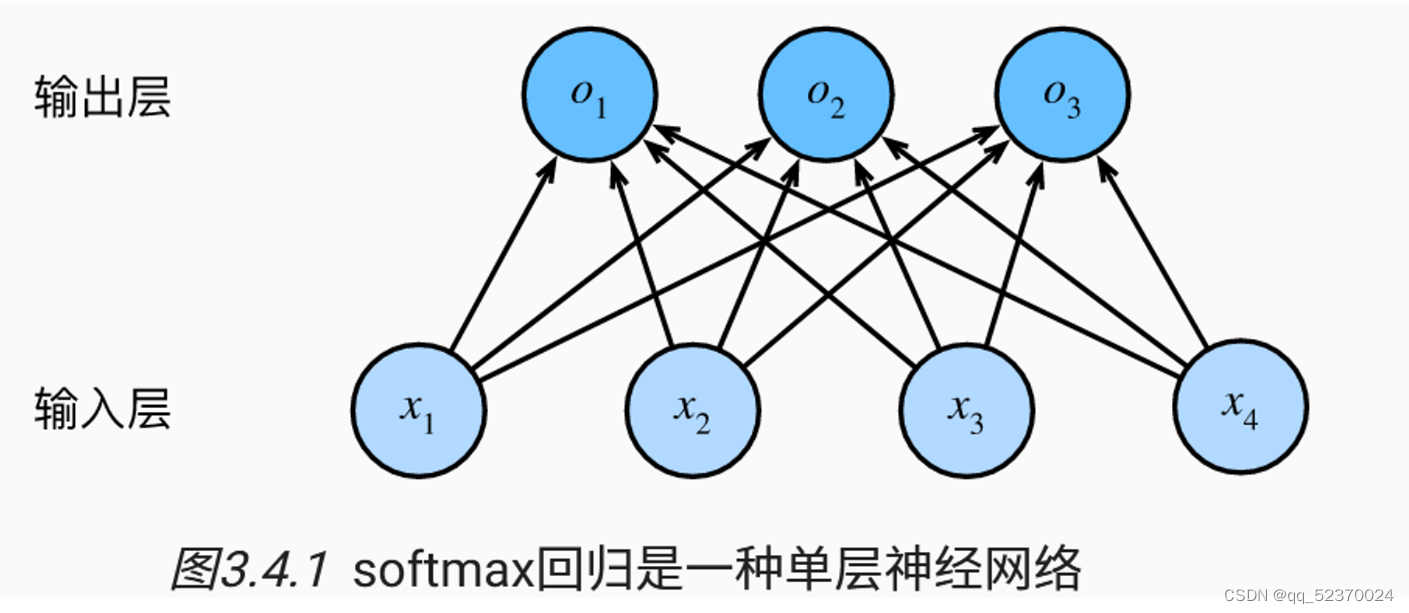
全连接层的参数开销
正如我们将在后续章节中看到的,在深度学习中,全连接层无处不在。 然而,顾名思义,全连接层是“完全”连接的,可能有很多可学习的参数。 具体来说,对于任何具有 d d d个输入和 q q q个输出的全连接层, 参数开销为 O ( d q ) O(dq) O(dq),这个数字在实践中可能高得令人望而却步。 幸运的是,将 d d d个输入转换为 q q q个输出的成本可以减少到 O ( d q n ) O(\frac{dq}{n}) O(ndq), 其中超参数 n n n可以由我们灵活指定,以在实际应用中平衡参数节约和模型有效性。
softmax运算

Huber’s Robust Loss
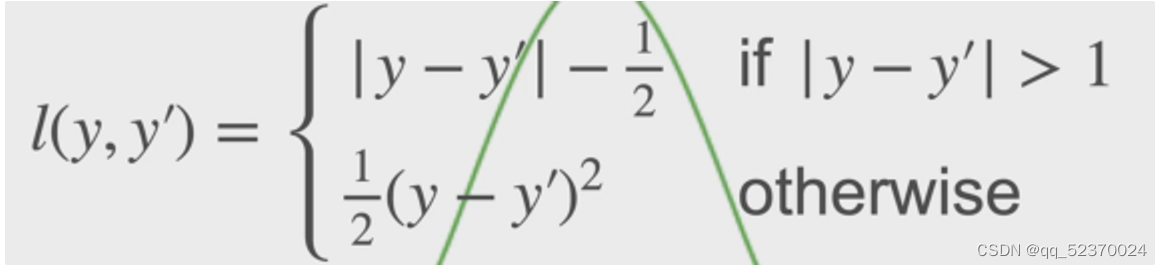
3.7 softmax回归的简洁实现
重新审视Softmax的实现