Stacked hourglass networks for human pose estimation
https://github.com/princeton-vl/pytorch_stacked_hourglass
这是一个用于人体姿态估计的模型，只能检测单个人
作者通过重复的bottom-up（高分辨率->低分辨率）和top-down（低分辨率->高分辨率）以及中间监督（深监督）来提升模型的性能

模型

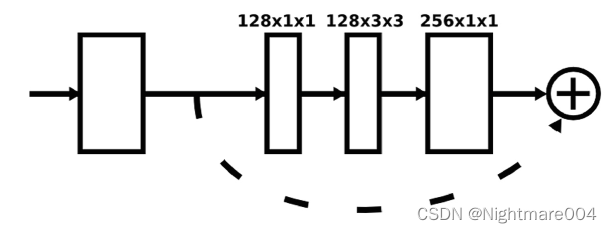
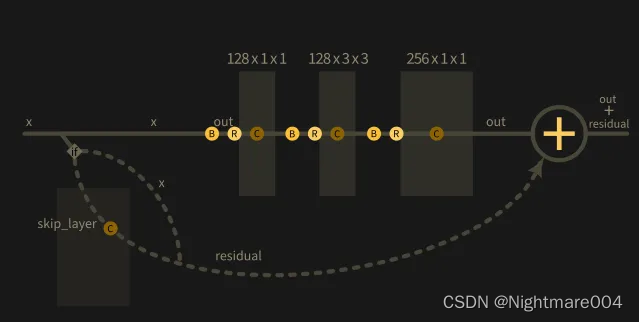
残差

模型里的残差都是不改变分辨率的

class Conv(nn.Module):
    def __init__(self, inp_dim, out_dim, kernel_size=3, stride=1, bn=False, relu=True):
        super(Conv, self).__init__()
        self.inp_dim = inp_dim
        self.conv = nn.Conv2d(inp_dim, out_dim, kernel_size, stride, padding=(kernel_size - 1) // 2, bias=True)
        self.relu = None
        self.bn = None
        if relu:
            self.relu = nn.ReLU()
        if bn:
            self.bn = nn.BatchNorm2d(out_dim)

    def forward(self, x):
        assert x.size()[1] == self.inp_dim, "{} {}".format(x.size()[1], self.inp_dim)
        x = self.conv(x)
        if self.bn is not None:
            x = self.bn(x)
        if self.relu is not None:
            x = self.relu(x)
        return x


class Residual(nn.Module):
    def __init__(self, inp_dim, out_dim):
        super(Residual, self).__init__()
        self.relu = nn.ReLU()
        self.bn1 = nn.BatchNorm2d(inp_dim)
        self.conv1 = Conv(inp_dim, out_dim // 2, 1, relu=False)
        self.bn2 = nn.BatchNorm2d(out_dim // 2)
        self.conv2 = Conv(out_dim // 2, out_dim // 2, 3, relu=False)
        self.bn3 = nn.BatchNorm2d(out_dim // 2)
        self.conv3 = Conv(out_dim // 2, out_dim, 1, relu=False)
        self.skip_layer = Conv(inp_dim, out_dim, 1, relu=False)
        if inp_dim == out_dim:
            self.need_skip = False
        else:
            self.need_skip = True

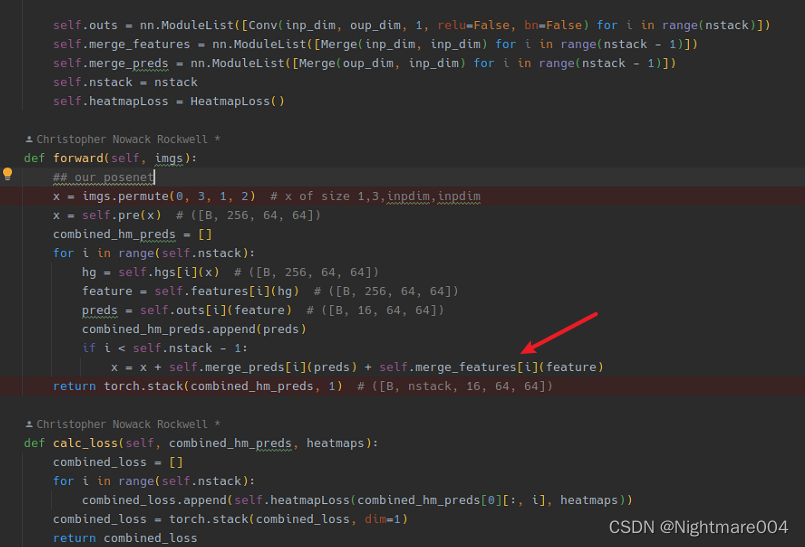
    def forward(self, x):  # ([1, inp_dim, H, W])
        if self.need_skip:
            residual = self.skip_layer(x)  # ([1, out_dim, H, W])
        else:
            residual = x  # ([1, out_dim, H, W])
        out = self.bn1(x)
        out = self.relu(out)
        out = self.conv1(out)  # ([1, out_dim / 2, H, W])

        out = self.bn2(out)
        out = self.relu(out)
        out = self.conv2(out)  # ([1, out_dim / 2, H, W])

        out = self.bn3(out)
        out = self.relu(out)
        out = self.conv3(out)  # ([1, out_dim, H, W])

        out += residual  # ([1, out_dim, H, W])
        return out  # ([1, out_dim, H, W])

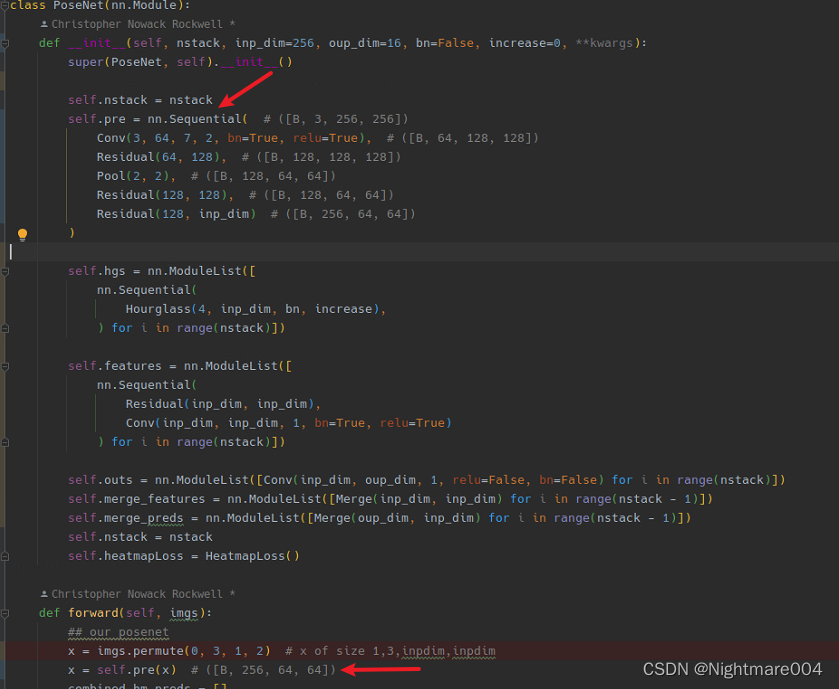
最前面

首先模型使用了一个卷积核为$7\ast 7$步长为2的卷积，然后使用了一个残差和下采样，将图像从$256\ast 256$降到了$64\ast 64$
接着接了两个残差

对应论文这一段

self.pre = nn.Sequential(  # ([B, 3, 256, 256])
            Conv(3, 64, 7, 2, bn=True, relu=True),  # ([B, 64, 128, 128])
            Residual(64, 128),  # ([B, 128, 128, 128])
            Pool(2, 2),  # ([B, 128, 64, 64])
            Residual(128, 128),  # ([B, 128, 64, 64])
            Residual(128, inp_dim)  # ([B, 256, 64, 64])
        )

单个Hourglass

在每一次最大池化之前，模型会产生一个分支，一条最大池化，另一条会接卷积（残差）
合并之前，走最大池化的的分支会做一次上采样，然后两个分支按元素加
（对应论文这两句）

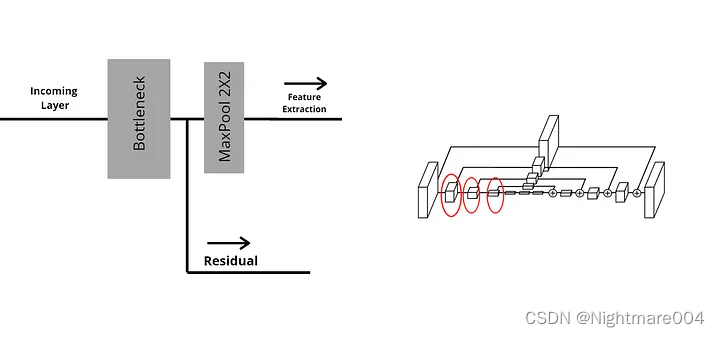
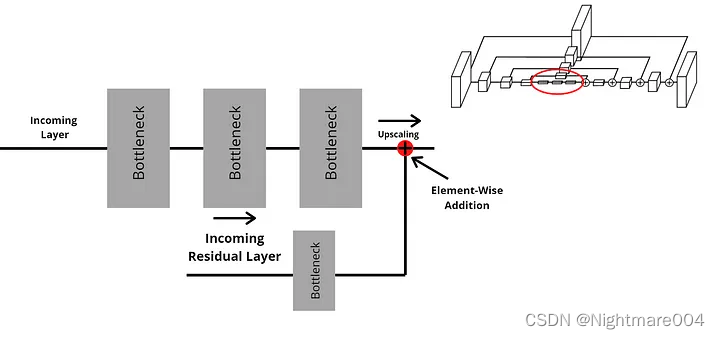
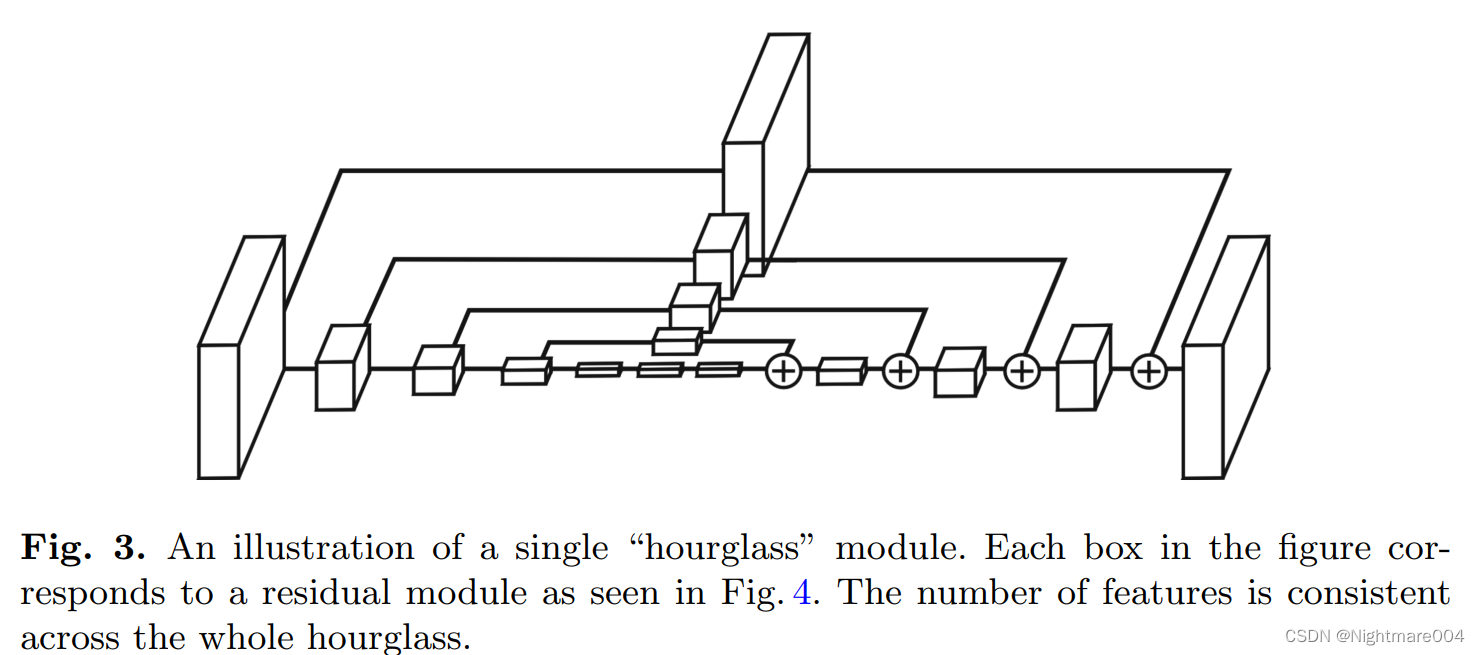
代码对应这个图
（然而论文的图里最前面的残差不知道怎么算。。。）

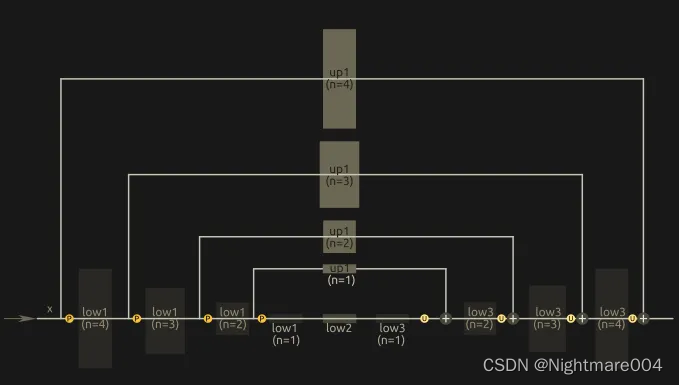
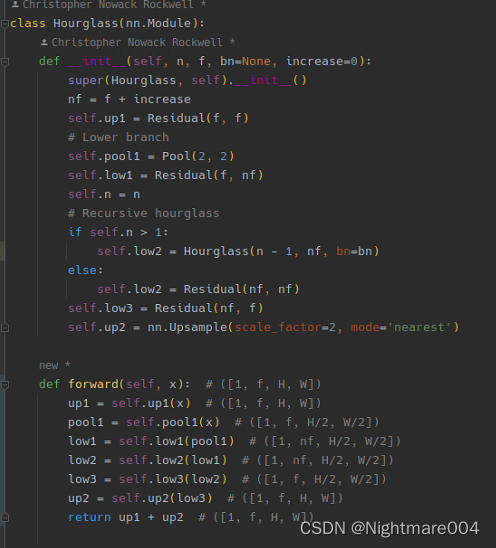
class Hourglass(nn.Module):
    def __init__(self, n, f, bn=None, increase=0):
        super(Hourglass, self).__init__()
        nf = f + increase
        self.up1 = Residual(f, f)
        # Lower branch
        self.pool1 = Pool(2, 2)
        self.low1 = Residual(f, nf)
        self.n = n
        # Recursive hourglass
        if self.n > 1:
            self.low2 = Hourglass(n - 1, nf, bn=bn)
        else:
            self.low2 = Residual(nf, nf)
        self.low3 = Residual(nf, f)
        self.up2 = nn.Upsample(scale_factor=2, mode='nearest')

    def forward(self, x):  # ([1, f, H, W])
        up1 = self.up1(x)  # ([1, f, H, W])
        pool1 = self.pool1(x)  # ([1, f, H/2, W/2])
        low1 = self.low1(pool1)  # ([1, nf, H/2, W/2])
        low2 = self.low2(low1)  # ([1, nf, H/2, W/2])
        low3 = self.low3(low2)  # ([1, f, H/2, W/2])
        up2 = self.up2(low3)  # ([1, f, H, W])
        return up1 + up2  # ([1, f, H, W])

热力图

模型会接两个$1\ast 1$的卷积来产生热力图（heatmap）

（虽然不知道为啥代码里还有一个残差）

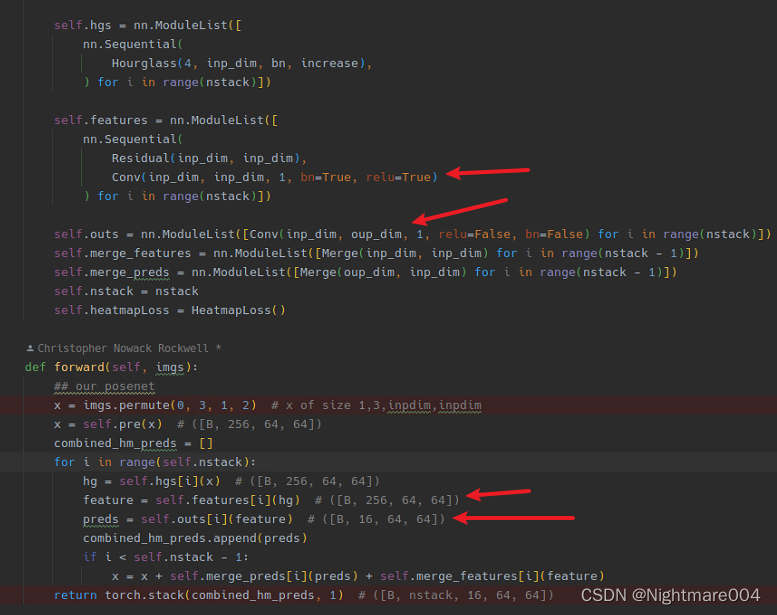
中间监督

将前一个Hourglass，heatmap，heatmap之前的特征通过2个$1\ast 1$的卷积加在一起

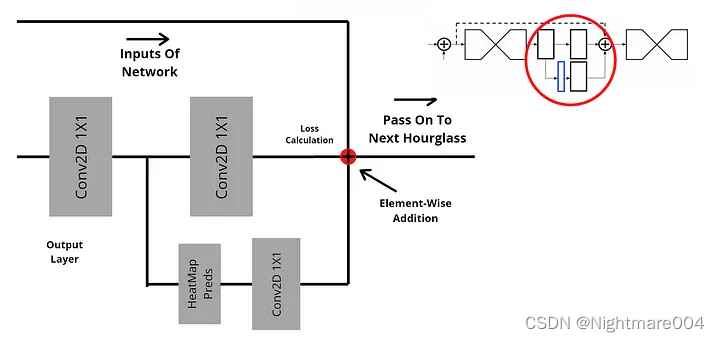
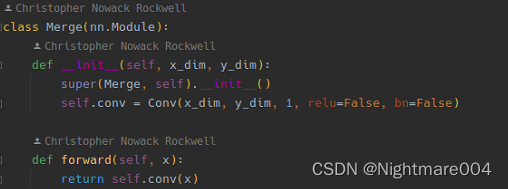
https://towardsdatascience.com/using-hourglass-networks-to-understand-human-poses-1e40e349fa15#:~:text=Hourglass%20networks%20are%20a%20type,image%20into%20a%20feature%20matrix.
https://medium.com/@monadsblog/stacked-hourglass-networks-14bee8c35678