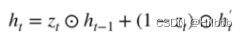YB菜菜的毫米波雷达自学之路(四)——浅谈角度模糊
- 前提说明
- 主要内容:
- 1. 一维平面天线阵列模糊函数及相关阐述
- 1.1角度模糊函数定义
- 1.2角度模糊函数案例与分析
- 1.2.1 雷达阵列信息
- 1.2.2 基础参数分析
- 1.2.3 模糊函数图与波束方向图的关系探索与疑问(接收角度)
- 2. 二维平面天线阵列模糊函数及相关阐述
- 2.1 案例
- 2.2 疑惑
前提说明
对目标的角度位置的明确估计是解决DoA估计问题的另一个基本要求。角度不模糊是用来描述:雷达天线系统唯一区分由目标反射回来的信号的DoA的能力。而雷达角度模糊函数(Angle ambiguity function)的引入,从某种程度上来说,就是为了明确雷达的不模糊视角。
需要注意的是,利用模糊函数来确定雷达的不模糊视野以及角度方面的参数需要确定一个大前提:
(1)假定影响雷达空间合成波束的唯一影响因素仅仅由天线位置造成,即,无论是MIMO模式还是BF模式,每个天线的单独波束图相同。
(2)远场环境,即,目标相对于天线之间的距离远大于天线孔径。此时,目标回波束可以看成平行,信号的传播方向对阵列的每个元素都是一样的。
主要内容:
(1)首先阐述一维度雷达角度模糊函数定义以及不模糊区间解释。
(2)阐述二维平面阵列角度模糊函数定义,以及模糊函数图。
(3)对于二维平面阵列的角度模糊函数的不模糊区间的选择存在疑问,希望有哪位雷达大佬可以给我一些解答。
(4)关于模糊函数与波束方向图展开了一点点的探索,是否正确有待考证
1. 一维平面天线阵列模糊函数及相关阐述
1.1角度模糊函数定义
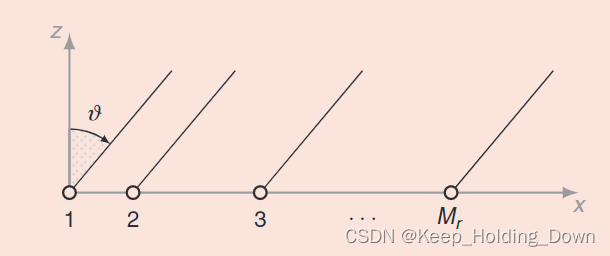
图1
图1展示了雷达一维天线阵列的布局(以接收角度),一个目标正处于相对于雷达中心的角度为
θ
\theta
θ的位置,并且有
M
r
M_{r}
Mr个接收天线。
需要注意的是:
(1)若雷达处于BF工作模式,则
M
r
M_{r}
Mr与实际接收天线数相同
(2)若雷达处于MIMO工作模式,则
M
r
M_{r}
Mr与总的虚拟阵列数相同
根据之前章节学习的内容,我们可以知道每个天线接收的信号之间存在一个相位差,而这个相位差可以表示为:
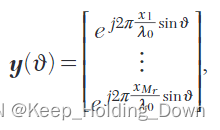
其中,
x
1
=
0
x_{1}=0
x1=0,
x
r
x_{r}
xr表示其于天线相对于基准天线的距离差。
不熟悉的可以参考之前的笔记:
浅谈雷达信号模型建立2
则,在一维阵列中,雷达的角度模糊函数
χ
\chi
χ可表达为:
χ
(
θ
i
,
θ
j
)
=
∣
y
(
θ
i
)
H
y
(
θ
j
)
∣
∣
∣
y
(
θ
i
)
∣
∣
∣
∣
y
(
θ
j
)
∣
∣
(
1
)
\chi(\theta_{i},\theta_{j})=\frac{|y(\theta_{i})^{H}y(\theta_{j})|}{||y(\theta_{i})||||y(\theta_{j})||} (1)
χ(θi,θj)=∣∣y(θi)∣∣∣∣y(θj)∣∣∣y(θi)Hy(θj)∣(1)
其中
θ
i
\theta_{i}
θi表示目标真实的DOA角度,而
θ
j
\theta_{j}
θj表示用于估计的DOA角度,角度分为为
(
−
9
0
o
,
9
0
°
)
(-90^{o},90^{°})
(−90o,90°)。
(
)
H
()^{H}
()H表示共轭,
∣
∣
.
∣
∣
||.||
∣∣.∣∣表示范数,在这里采用2范数,即向量的模值。
通过角度模糊函数绘制出的角度模糊点云图反映了当前阵列的角度信息,即:最大不模糊区间、角度分辨率、以及栅瓣出现的位置。
1.2角度模糊函数案例与分析
1.2.1 雷达阵列信息
(1)首先给出雷达阵列信息:
发射天线位置:[0, 2.54](单位
λ
\lambda
λ)
接收天线阵列:[0 1.88 3.32](单位
λ
\lambda
λ)
(2)模糊函数公式中,角度步进最小单位为1°。
1.2.2 基础参数分析
根据公式(1),我们绘制雷达模糊函数图,其中角度步进值为
1
°
1°
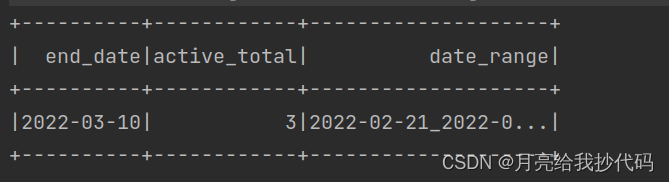
1°,角度搜索范围为(-90~90),因此数值从0到180。绘制后的结果如图2(a)所示。
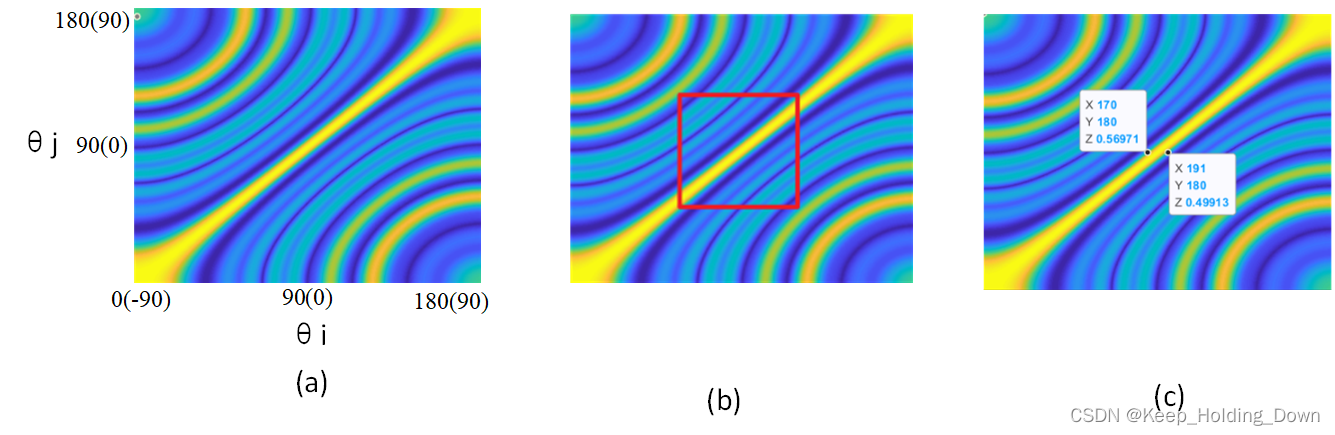
图2 雷达模糊函数图
(1)分析图2(a):
我们知道,当
θ
j
\theta_{j}
θj(估计角度)=
θ
i
\theta_{i}
θi(真实角度)的情况下,自相关应该返回最大值1。因此在模糊图2(a)中,存在一个高亮的黄色斜线段,因为在这条斜线上是代表
θ
j
=
θ
i
\theta_{j}=\theta_{i}
θj=θi的情况。
(2)分析雷达角度不模糊区域(分析图2(b))
理想情况下,只有在
θ
j
=
θ
i
\theta_{j}=\theta_{i}
θj=θi的情况下,自相关应该返回最大值1,其他情况下都是0。若
θ
j
!
=
θ
i
\theta_{j}!=\theta_{i}
θj!=θi时也存在较高的相关峰值,那么雷达就存在角度模糊性。基于这点,我们可以根据相关值1和0的分布来确定无歧义区域。
从角度模糊图可知,存在
θ
j
!
=
θ
i
\theta_{j}!=\theta_{i}
θj!=θi区域具备较高的相关峰值(以-6dB(T=0.5)为门限作为评判标准)。
为寻找不模糊角度范围,需要以0度为中心画一个矩形框,在这个框中不能存在额外的相关峰高于门限的区域。如图2(b)所示,该阵列雷达的不模糊角度范围为红色的正方形延伸的宽度。
注: 需要注意的是,相关峰门限的选择会影响雷达最大不模糊角度的区间,这是因为不同应用场景中对信号的要求不一样,一些情况下门限可能选择-3dB,也有选择-6dB作为门限,甚至有选择-8dB作为门限。
(3)雷达角度分辨率(分析图(c))
通过前面的分析我们知道,雷达模糊图中间的斜着的亮线是
θ
j
=
θ
i
\theta_{j}=\theta_{i}
θj=θi的情况,因为角度相同所以自相关值为1.但它并不是理想的”细线“,而是一个想外延展的”粗线段“,而这个粗线段反映了雷达的角度分辨率。考虑到角度分辨率存在小数,这里图中的角度搜索步进是
0.
5
o
0.5^{o}
0.5o
从图像上观察: 如图(C),我们以-6dB为门限,可以看出,以0为中心,向两边扩展的范围是:
10.
5
o
10.5^{o}
10.5o(角度分辨率)。
理论计算:
1.22
∗
λ
D
∗
180
/
p
i
≈
11.
9
o
1.22*\frac{\lambda}{D}*180/pi \approx11.9^{o}
1.22∗Dλ∗180/pi≈11.9o
注:这里的雷达角度分辨率与之前的角度分辨率计算方式有区别,其根本原因是天线布局是否均匀。在均匀阵列中,我们可以用 λ D ∗ 180 π \frac{\lambda}{D}*\frac{180}{\pi} Dλ∗π180来计算,当天线阵列非均匀时,通常采用 1.22 ∗ λ D ∗ 180 / p i 1.22*\frac{\lambda}{D}*180/pi 1.22∗Dλ∗180/pi来计算。
1.2.3 模糊函数图与波束方向图的关系探索与疑问(接收角度)
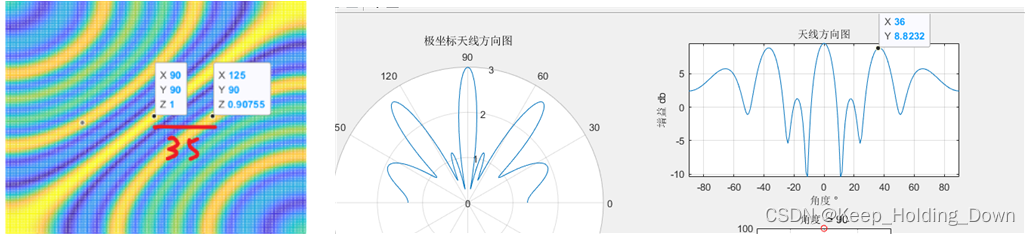
图3
在BF模式下,我们通常通过波束方向图来判断天线在空间中的合成波束情况,利用波束方向图我们可以看出当前阵列在空间中的波束峰值指向、栅瓣位置、旁瓣大小等。其功能和模糊函数方向图相似。
在BF模式下,所有发射天线同时发射波束,因此可以等效成一根发射天线,此时阵列可以等效为:
发射天线位置:[0](单位
λ
\lambda
λ)
接收天线阵列:[0 1.88 3.32](单位
λ
\lambda
λ)
利用模糊函数公式和天线方向图生成公式,可以得到当前天线阵列在接收端的模糊函数图和接收天线阵列的波束方向图,如图3所示。
似乎可以得到这么一个结论:
**从模糊图观察:**以0点为中心,向两个视角方向扩展,达到下一个相关峰超过门限的角度范围为:
3
5
o
35^{o}
35o
从波束方向图观察 当前接收天线阵列的栅瓣位置相对于主瓣偏差近似
35
°
35°
35°。
两者近似。
但是存在两个问题:
(1)在BF模式下,模糊函数图似乎不能观察发射阵列的情况,事实上,发射阵列也同样影响雷达模糊区间,发射阵列的栅瓣也会影响接收信号的质量。
(2)以0点横向扩展的方式与模糊区间矩形扩展的方式不同,如何统一,这是当前我没有弄明白的问题。
2. 二维平面天线阵列模糊函数及相关阐述
二维平面阵列的模糊函数公式其实并不难理解,其详细的阐述可参考论文:
DI SERIO, ADOLFO, HUEGLER, PHILIPP, ROOS, FABIAN, et al. 2-D MIMO Radar: A Method for Array Performance Assessment and Design of a Planar Antenna Array[J]. IEEE Transactions on Antennas and Propagation,2020,68(6):4604-4616. DOI:10.1109/TAP.2020.2972643.
这里直接给出公式结论:
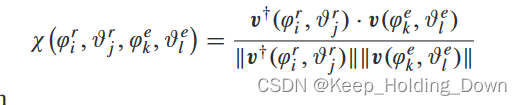
其中,这里的
v
v
v与前文的
y
y
y是同一个含义,只不过增加了俯仰角度,即:
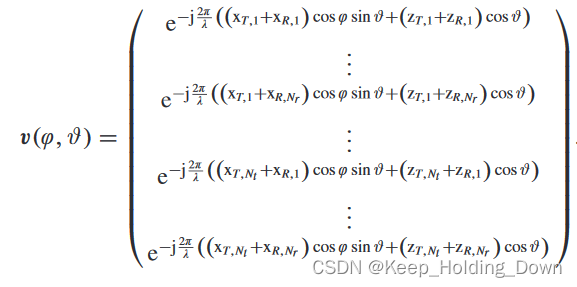
从公式角度上可以看出,二维模糊函数与一维度模糊函数相似。
但存在区别:在一维模糊函数中,由于只有一个方向维度,因此只需要进行一个维度的搜索,即,模糊函数图是一个二维矩阵(命名为
X
X
X)。
但,在平面阵列中,模糊函数的角度搜索为2个维度(方位维度和俯仰维度),因此模糊函数图是由多个二维局部矩阵(
X
X
X)构成的大矩阵
H
H
H,其表达式为:
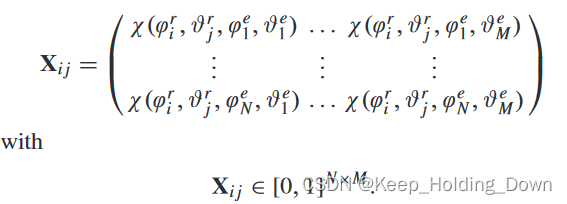
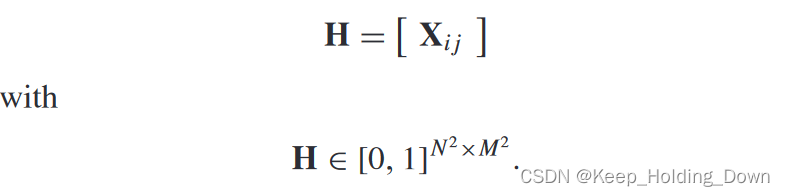
2.1 案例
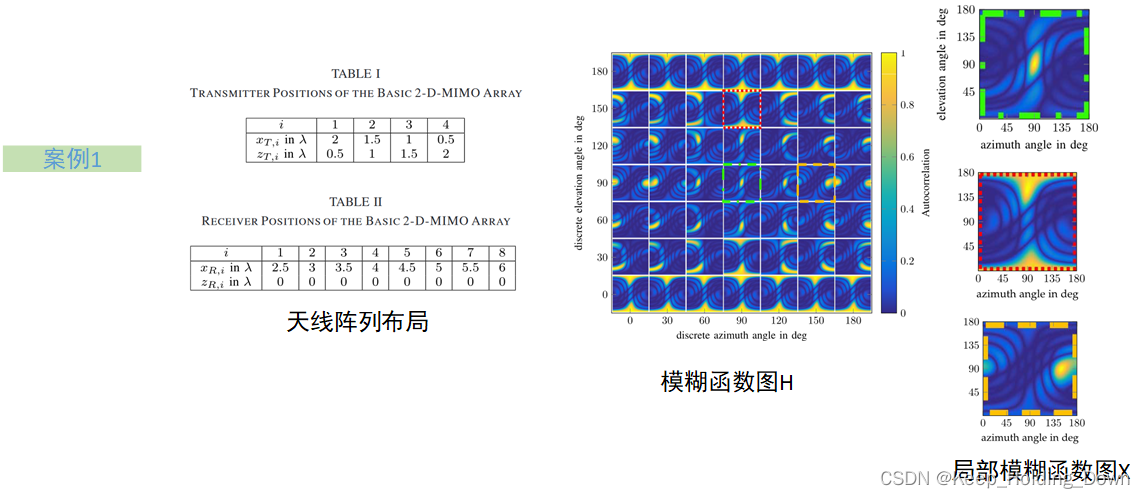
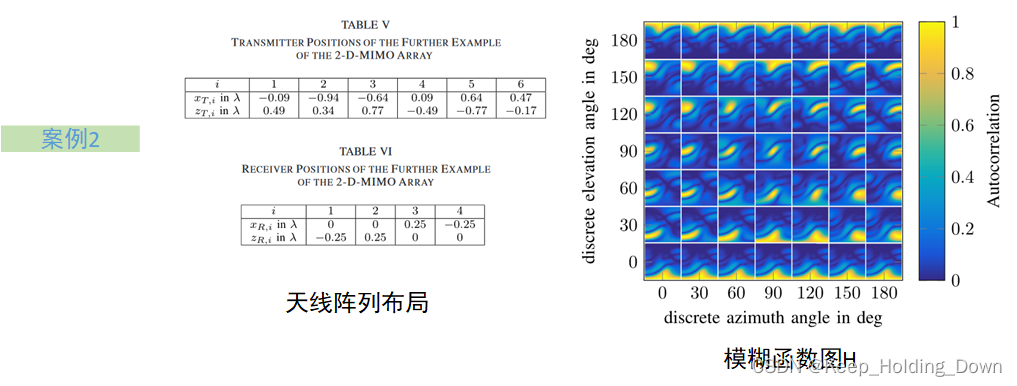
图4
可以看出相比于一维,二维多了一个俯仰维度的搜索,因此模糊函数图从原本的单一的二维矩阵图,变成二维矩图阵组。每一个局部二维矩阵图可以看作确定俯仰角后的一维模糊函数搜索。
2.2 疑惑
论文中,设定旁瓣阈值为0.5,然后通过模糊函数图H得到模糊索引矩阵Q,以(0,0)为中心向方向维度和俯仰维度扩展,得到当前阵列最大不模糊区间,如图。
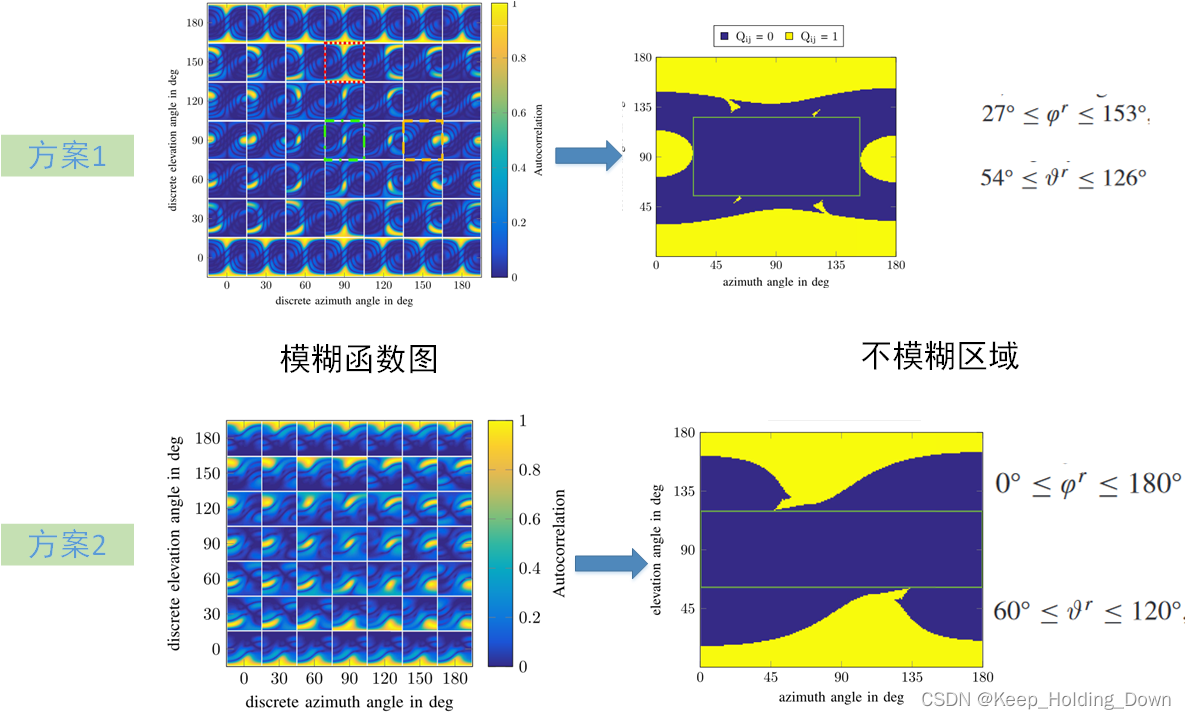
图5
虽然我仿真出来了模糊函数图H,但是不明白如何得从H图到模糊索引矩阵Q。如果有哪位大佬懂这个,如果可以麻烦指导一下。如果有同样感兴趣的伙伴,可以联系一起讨论

![②【Java 组】蓝桥杯省赛真题解析 [振兴中华] [三部排序] 持续更新中...](https://img-blog.csdnimg.cn/20a7f1b58dfb4660b75d7f021c157d57.png#pic_center)