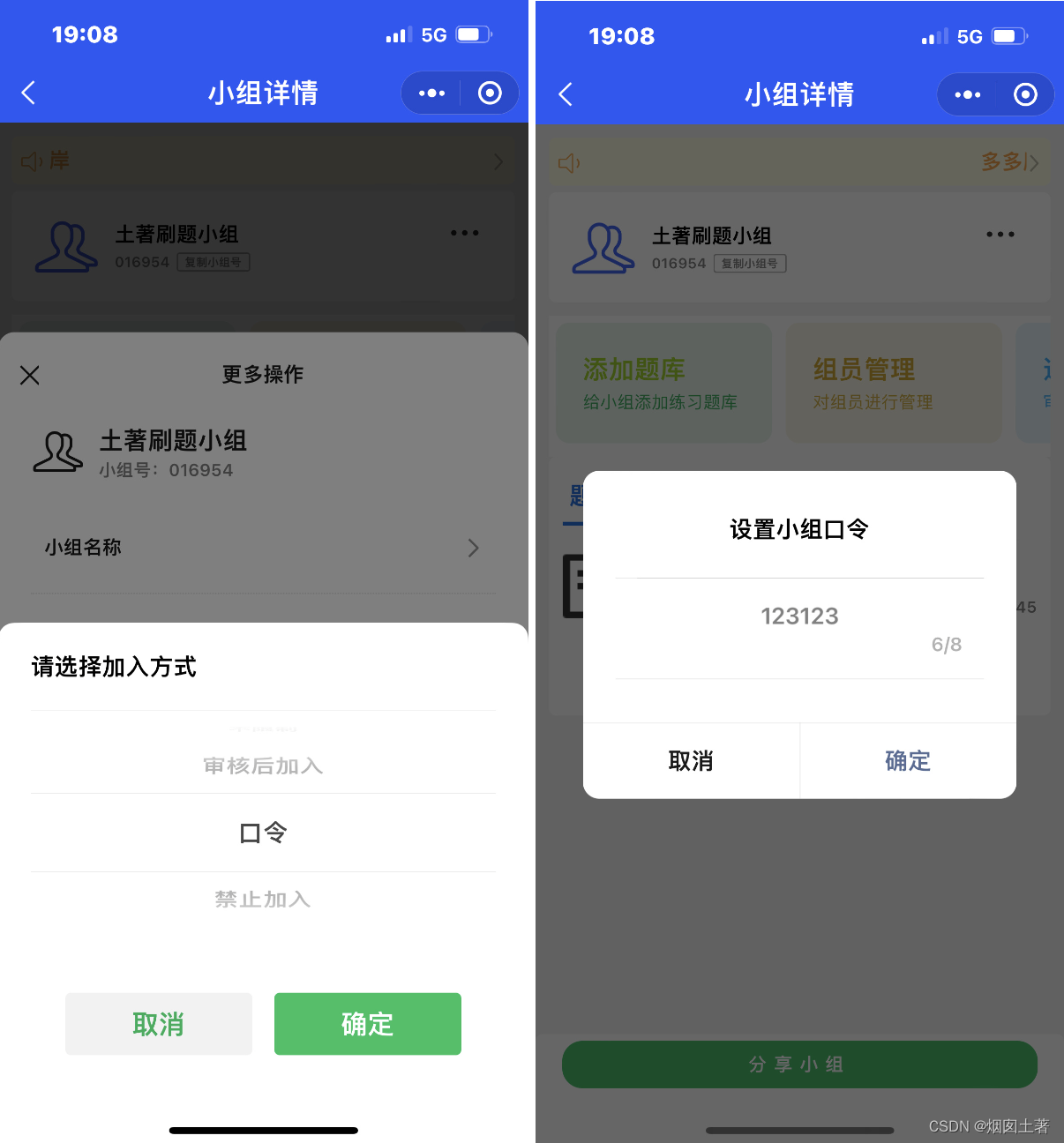
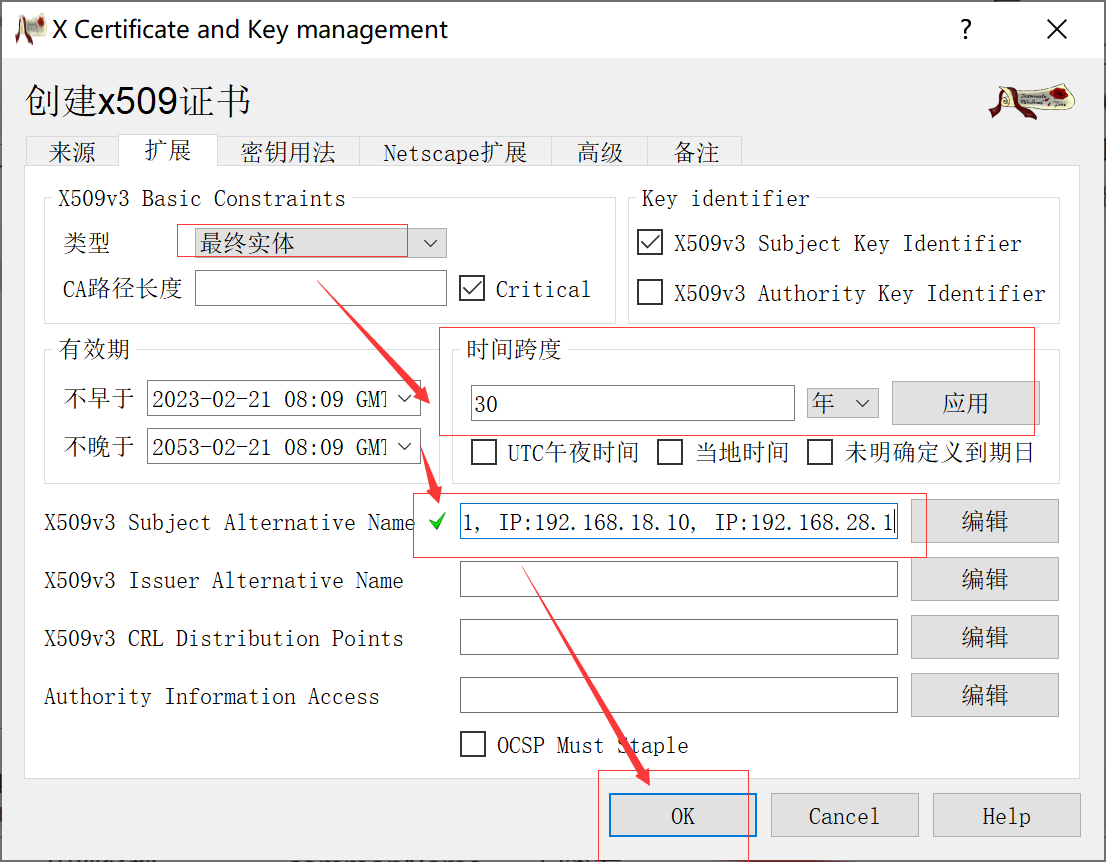
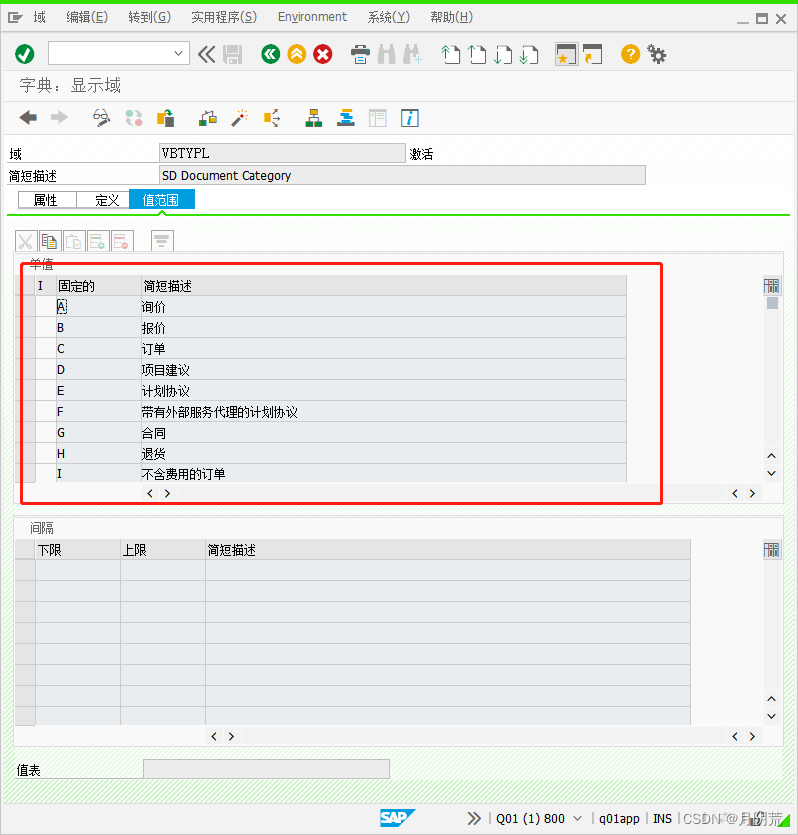
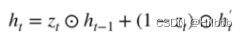个人简介:Java领域新星创作者;阿里云技术博主、星级博主、专家博主;正在Java学习的路上摸爬滚打,记录学习的过程~
个人主页:.29.的博客
学习社区:进去逛一逛~
蓝桥杯真题--持续更新中...
- 一、振兴中华
- 二、三部排序(代码填空题)
一、振兴中华
题目描述:
文字版:
小明参加了学校的趣味运动会,其中的一个项目是:跳格子。
地上画着一些格子,每个格子里写一个字,如下所示:
从 我 做 起 振
我 做 起 振 兴
做 起 振 兴 中
起 振 兴 中 华
比赛时,先站在左上角的写着“从”字的格子里,可以横向或纵向跳到相邻的格子里,但不能跳到对角的格子或其它位置。一直要跳到“华”字结束。
要求跳过的路线刚好构成“从我做起振兴中华”这句话。
请你帮助小明算一算他一共有多少种可能的跳跃路线呢?
解题思路:
借助递归的思想解题,
第一次跳格子选择只有两种情况:
①向右跳
②向下跳
之后的每一个格子也都是只有上述两种选择,我们设定一个函数,函数中的两个参数代表跳格子的方向,以参数对应的坐标(0,0)作为开始位置,通过递归来遍历所有跳格子的选择,当x轴下标到4,或Y轴下标到3时,就可以认定为一条路线,并返回1,作为累加的次数。
解题代码:
public class 振兴中华 {
public static void main(String[] args) {
int answer = dfs(0,0);
System.out.print(answer);
}
public static int dfs(int x,int y) {
if(x == 4 || y == 3) return 1; //当x轴下标到4,或Y轴下标到3时,就可以认定为一条路线
return dfs(x+1,y) + dfs(x,y+1);//递归,开始向右跳得到的路线 + 看是向左跳得到的路线,从而获取的所有路线
}
}
二、三部排序(代码填空题)
题目描述:
文字版:
一般的排序有许多经典算法,如快速排序、希尔排序等。
但实际应用时,经常会或多或少有一些特殊的要求。我们没必要套用那些经典算法,可以根据实际情况建立更好的解法。
比如,对一个整型数组中的数字进行分类排序:
使得负数都靠左端,正数都靠右端,0 在中部。注意问题的特点是:负数区域和正数区域内并不要求有序。可以利用这个特点通过 1 次线性扫描就结束战斗!!
以下的程序实现了该目标。
其中 x 指向待排序的整型数组,len 是数组的长度。
请分析代码逻辑,并推测划线处的代码。
源代码(java):
import java.util.*;
public class Main
{
static void sort(int[] x)
{
int p = 0;
int left = 0;
int right = x.length-1;
while(p<=right){
if(x[p]<0){
int t = x[left];
x[left] = x[p];
x[p] = t;
left++;
p++;
}
else if(x[p]>0){
int t = x[right];
x[right] = x[p];
x[p] = t;
right--;
//p++;
}
else{
______________;
}
}
show(x);
}
static void show(int[] x)
{
for(int i=0; i<x.length; i++)
{
System.out.print(x[i] + ",");
}
System.out.println();
}
public static void main(String[] args)
{
//int[] x = {25,18,-2,0,16,-5,33,21,0,19,-16,25,-3,0};
sort(new int[]{-1,0,1,-2,0,2,-3,0,0,3,-4,-5,4,-6,0,5,6});
sort(new int[]{-1,0,-1,-2,0,-2,-3,0,0,-3,-4,-5,-4,-6,0,-5,-6});
sort(new int[]{1,0,1,2,0,2,3,0,0,3,4,5,4,6,0,5,6});
}
}
解题思路:
代码中的这一段,是将 < 0 的数放到左边,然后 l和p 都加一 :
while(p<=right){
if(x[p]<0){ //若数小于0
//将最左边数与当前数调换位置
int t = x[left];
x[left] = x[p];
x[p] = t;
//左边界后移一位
left++;
//p位置也后移一位
p++;
}
紧接着就是将 >0 的数,与右边界上的数调换位置(调换后p位置不用动,右边界向前移动一位)
else if(x[p]>0){
int t = x[right];
x[right] = x[p];
x[p] = t;
right--;
//p++;
}
那么画线位置,自然就是当p位置的数 =0 时,需要做操作。 这时候p位置的数既不大于零也不小于零,所以左右边界不用动,只需要p向后挪动一位,继续下一次的判断即可。
解题代码:
p++;