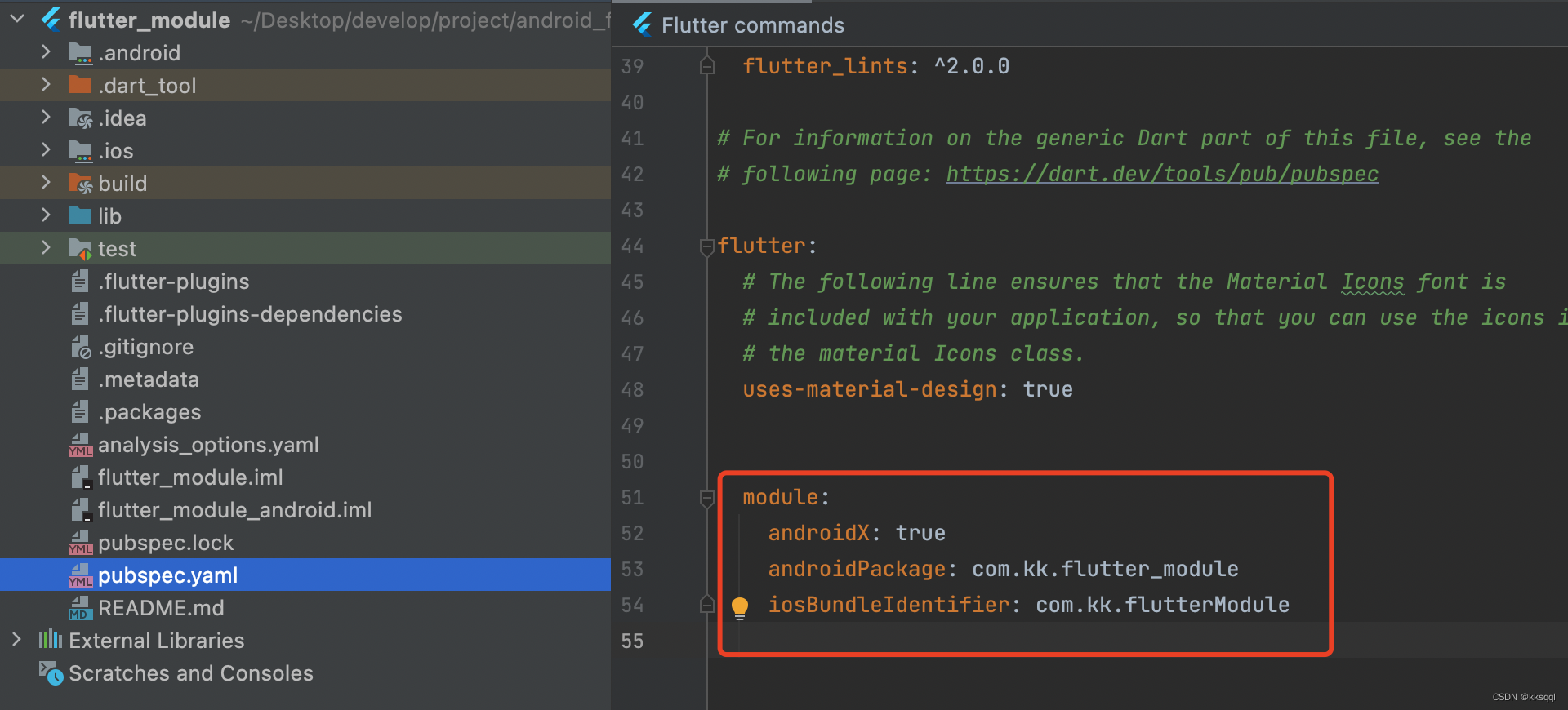
说明

介绍 $1 - bi t$ 论文内容。
原文链接：1-bit stochastic gradient descent and its application to data-parallel distributed training of speech DNNs | Semantic Scholar

ABS

实验证明在分布式机器学习的过程中能够通过将同步所传递的梯度进行量化（从 $32$ 位到 $1$ 位），同时加上量化容错机制能够很好的加快整个训练过程。最值得注意的时，模型的收敛情况并没有收到影响。

本文将该发现与 $SG D, A d a G r a d$ , 自动批量选择, 双缓冲区,模型并行技术相结合设计了。意料之外的是，量化甚至能让精度有一个很小的提升。

不同的模型在使用该方法后加速效果明显。

1 Introduction and Related Work

现在上下文相关的深度神经网络模型基本都是通过反向传播进行训练（常用的例如 $SG D$ ），而上述的模型的训练是非常耗时的。

注：上下文相关的神经网络应该是指类似与解决翻译问题所用的模型。

使用分布式训练上述的模型已经取得了一定成功。（这里介绍了一部分相关工作，这里不进行赘述）

在分布式训练中，一个非常重要的问题就是带宽瓶颈的问题：即各个节点训练一定时间之后需要进行数据的发送（这不管是模型并行还是数据并行都会发生），而这个过程交换的数据量往往取决于模型的大小，而现在使用的模型一般都比较大，所以网络的带宽成为了分布式机器学习的一个瓶颈。

缓解这个方法一般有两类方法：

增加批量大小，这样每轮会进行的计算会增加，而参与通信的时间会相对减少；
减少每一次通信的数据交换量。

本文提出的方法属于第二种，同时本文更多关注的是将量化方法应用于数据并行的分布式训练中。

2 Data-Parallel Deterministically Distributed SGD Training

通常采用 $BP$ 进行模型的训练，过程可以被概述为下列的两个方程：
$KaTeX parse error: Undefined control sequence: \part at position 114: …^{t+N-1}\frac {\̲p̲a̲r̲t̲ ̲F_{\lambda}(o(\…$
上述过程对应反向传播求导和梯度下降进行更新。

2.1 Data-Parallel Distributed SGD

上述的方程可以进行分布式计算，只需要将方程 $(2)$ 的梯度计算部分按照节点的个数，让每个处理一部分数据，然后进行梯度的计算，计算完成后，相加即可得到某个时刻的梯度。

$perfect\ overlap$ ：选取合适的工作节点个数能够让计算和数据交换进行最优的并行化，也就是通信资源和计算资源同时饱和。
$T_{calc}(\hat K)=T_{comm}(\hat K)$
也就是选取 $K$ 让每轮的通信时间和计算时间相等，这样当通信完成是下一轮的计算也完成可以继续进行通信。

计算时间可以被分解成固定的计算时间和可变的计算时间两部分。固定的计算时间一般是完成一些必要的操作时间所花费的时间，而可变计算时间往往会根据模型的大小，批量大小发生改变。

$Figure\ 1$ 展示了当节点个数下降到通信时间与计算时间相等时获得的加速。

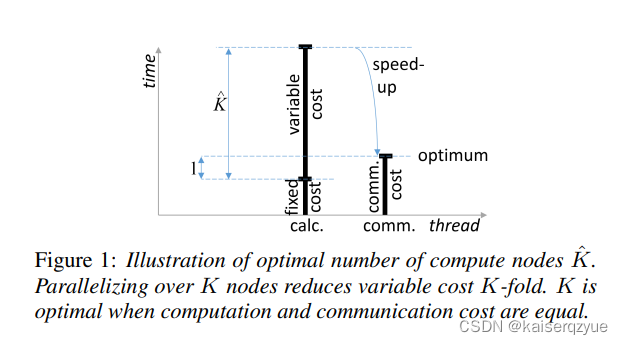
在这里插入图片描述

$\hat K$ 可以通过如下公式进行计算：
$\hat K = \frac {N/2*T^{frm}_{calc}+C*T^{post}_{calc}}{\frac 1 ZT^{float}_{comm}-T^{upd}_{calc}}$
各参数的含义：（设模型的大小为 $M$ ）

$N$ ：批量的大小。
$T^{frm}_{calc}$ ：计算梯度所花费的时间，大约为 $\frac M {FLOPS}$ 。
$C$ ：一个常量，使用特殊方法处理所携带的常数。
$T^{post}_{calc}$ ：后续进行处理所需要的时间，例如使用 $A d a G r a d, m o m e n t u m$ 需要花费的额外时间（需要和 $C$ 相乘才能获取实际时间），大约为 $\frac M r$ ， $r$ 为内存的带宽。
$Z$ ：数据传输之前的压缩率，在本文中将 $32$ 位压缩成 $1$ 位，那么 $Z = 32$ 。
$T_{comm}^{float}$ ：不压缩梯度进行通信所需要花费的时间，大约为 $\frac M b$ ， $b$ 为两个结点之间的网络带宽。
$T^{upd}_{calc}$ ：参数服务器将受到的梯度用于更新所需要的时间，大约为 $\frac M r$ 。

上面的公式的理解：

分母是实际进行通信的时间，分子计算所有 $N$ 个数据会花费的时间，而前面的推断需要让每个结点的计算时间和通信时间相等，由于在分布式机器学习中每个结点拥有的数据量是相同的，所以分子的计算时间除以 $K$ 就是每个结点的计算时间，让两者相等并将 $K$ 移到方程的一边即可得到上面的公式。上面计算时间的计算出现了一个除以 $2$ ，这在下一小节会解释。

2.2 Double Buffering with Half Batches

上一节的公式里面出现了除以 $2$ 是因为使用了双缓冲区。整个过程将每一个批量会分成大小相等的两部分放入缓冲区中，当前一部分计算完成后，开始计算后一部分，这个时候前一部分即可进行通信，当后一部分计算完成的时候，即可进行通信，此时又可以从缓冲区读取下一个批量的前一部分，所以每次实际上只计算了整个批量的一半，所以上面会出现除以 $2$ 。

2.3 Potential Faster-Than-Fixed-Cost Communication

当通信时间降到固定计算时间之下时，那么此时上面的计算公式将不再适用。此时整个系统的限制在于固定的计算时间，通信很难饱和。此时在使用双缓冲区就没有什么意义了，因为此时的通信带宽是足够的，而双缓冲区是为了缓解通信的压力。

2.4 Relation to Hogwild/ASGD

异步更新能够增加并行度，但是并没有改变基础性的东西。

3 1-Bit SGD with Error Feedback

将需要交换的数据进行压缩，将其压缩为一位的数据，这样能够减少数据的交换量，从而减少通信的瓶颈。

不过如果只是简单的将数据压缩成一位，然后任由 $SG D$ 进行缺失数据的修正，那么这是很容易导致模型发散的。

为了防止模型的发散提出了错误反馈机制，该机制并不会将丢失的精度给丢弃掉，而是会对其进行记录下一次更新的时候需要同时考虑之前丢失的精度。

整个过程可以用下面的公式来表述：
$\begin{aligned} &G^{quant}(t) = Q(G(t)+\Delta(t-N))\\ &\Delta(t)=G(t)-Q^{-1}(G^{quant}(t)) \end{aligned}$
参数说明：

$G$ ：本轮计算出来的梯度。
$Q$ ：量化函数，具体的，如果输入大于 $0$ ，则量化成 $1$ ，输出小于 $0$ ，则量化成 $0$ ，这样就可以将原本需要用 $32$ 位表示的梯度只用 $1$ 位进行表示。
$G^{quant}$ ：量化后的梯度。
$Q^{-1}$ ：反量化函数，输入只能是 $0$ 或者 $1$ ，当输入是 $1$ 的时候输出是 $1$ ，当输入是 $0$ 的时候，输出是 $- 1$ 。
$\Delta$ ：梯度误差。

上述的过程就是压缩之后会记录压缩误差，压缩误差在下一轮的时候继续参与压缩。

3.1 Aggregating the Gradients

本文使用的聚合算法的复杂度关于结点个数是 $O (1)$ （这里的描述有一点奇怪，但是大概的意思就是每个结点聚合的数据量为所有梯度的一部分）。

具体的过程如下：

如果有 $K$ 个结点，那么每个结点会处理 $\frac 1 K$ 的梯度。
每个结点会从其他的 $K - 1$ 个结点接收属于自己处理的梯度部分。
收到后结点聚合自己负责的这一部分梯度。
聚合完成后分发给其他所有结点。

4 System Description

根据最佳节点个数的计算公式，至少存在三种方法能够提升并行度：（也就是通过改变变量让公式的结果变大）

提升 $N$ ：增加每轮处理的批量个数。
增加 $Z$ ：增加压缩度。
减少固定计算时间（固定计算时间减少意味着相同的计算时间中有更多的时间用于了梯度的计算）

本文的压缩算法属于第二种方法。

对于方法一本文的实验发现 $N$ 的增加是有一个限制的，当增大的太多时，整个模型可能会发散。同时本文发现一个成熟的模型能够处理的 $N$ 的值要大一些。

为了防止模型发散的情况，本文后面的实验会隔一定的时间增大 $N$ 而不是一开始就将 $N$ 设置的很大，这样能够防止模型发散或是准确率下降严重。

除了这些之外，学习率也是采用递减的方式。

最后使用了 $A d a G r a d$ 进行优化，这样模型会收敛的更快，同时这也使得批量大小能够进一步的增加。

本文的系统可以在三个不同的地方使用 $A d a G r a d$ ：

在本地梯度量化之前；（可能会导致不一致性，但是可能对量化有益）
聚合结束后的数据交换期间；（可能会与量化冲突）
使用动量平滑后；（可以减少内存的使用和固定计算时间但是效果不好，因为峰值被动量磨平了）

作者发现 $A d a G r a d$ 在量化后动量平滑前使用效果最好。

为了也利用方法 $3$ ，本文在使用数据并行的同时，在多 $GP U$ 上做了模型并行。

5 Experimental Results

实验的细节可以在原文中找到。
论文的实验做的都是语音识别相关的，所以并没有证明所有方面都适合该方法。

5.1 Cost Measurements

这一部分主要测量几个耗时。

$T^{float}_{comm}$ 大约为 $3 - 10 m s$ $。

$T^{post}_{calc}+T^{upd}_{calc}=18.2ms$ 。

$T^{upd}_{calc}\approx9$ 。

$Table\ 1$ 给出了 $T^{frm}_{calc}$ 与批量大小的关系。

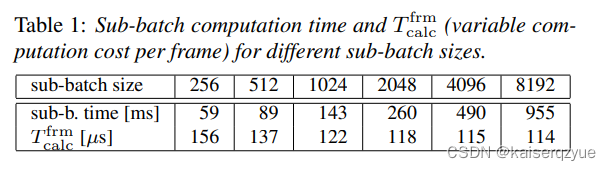
在这里插入图片描述

5.2 Effect of 1-Bit Quantization

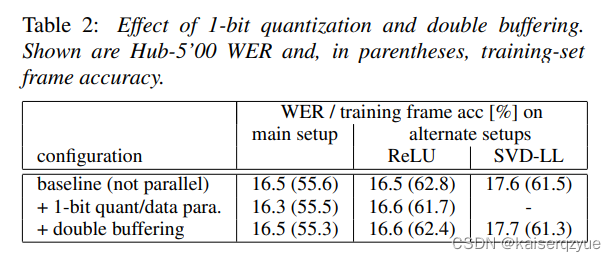
$Table\ 2$ 展示了不同的模式下的三种方式的对比，可以看出 $1 - bi t$ 的效果并没有受到太大的影响。

在这里插入图片描述

5.3 When to do AdaGrad?

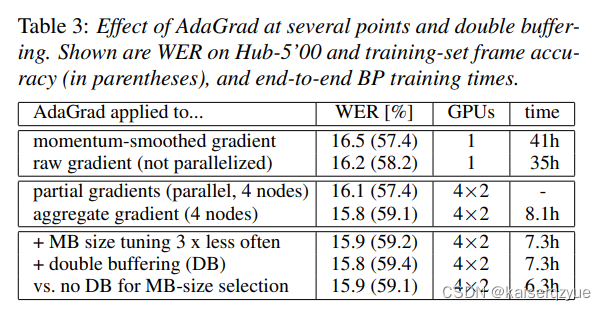
$Table\ 3$ 展示了在不同环节使用 $A d a G r a d$ 进行优化对于准确率的影响，可以看出应该在动量平衡之前使用错误率会更低，作者指出这可能是因为动量平滑减少了梯度的标准差从而导致 $A d a G r a d$ 的效果不好。

$partial\ gradients$ 代表量化前各个结点自身的梯度， $aggregate\ gradient$ 代表量化后聚合的梯度。

在这里插入图片描述

5.4 Impact of MB-Size Selection and Double Buffering

这一部分讲的是选取特别大的批量的时间耗时。从 $Table\ 3$ 中每一栏花费的时间可以得到一些信息。

第二行的时间比第一行小主要是因为：第一行的实验选取了较大的批量大小。

第四行增加到了四个结点进行数据进行，同时每个结点进行两个 $GP U$ 的模型并行导致整个的时间下降到 $8.1 h$ .

第五行相比于第四行的下降则是因为第四行的实验每 $24 h$ 选择一次新的批量大小，而第五行每 $72 h$ 选择一次。

第六行与第五行对比可以发现在这种情况下并没有进一步带来速度的提升，不过当使用双重缓冲区了之后自动选择的批量大小将会有所下降。

第七行代表的是什么意思本人并没有看懂。

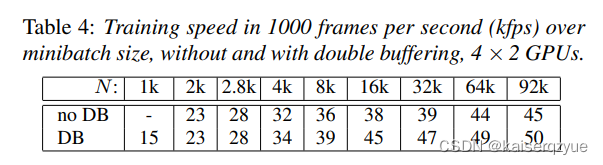
$Table\ 4$ 展示了固定不同的批量大小下双重缓冲对于速度的影响。

在这里插入图片描述

5.5 Combination with Model Parallelism

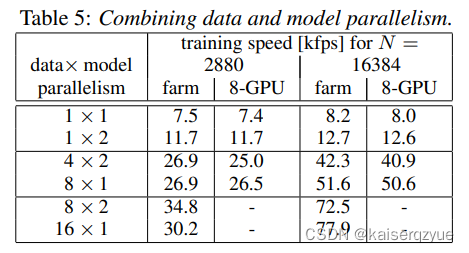
下图展示了不同的数据并行与模型并行的速率，可以发现在显卡数量相同的情况下，只有 $8\times2$ 的时候模型并行提升了速率，在大多数情况下模型并并没有提升速率，这代表着在大多数情况下模型并行没有数据并行高效，这是因为如果使用模型并行则不能很好的利用缓存机制，模型并行的时候，每交换一次数据缓冲就会失效，而如果是更多的使用数据并行，那么就会减少一定缓存失效的次数。

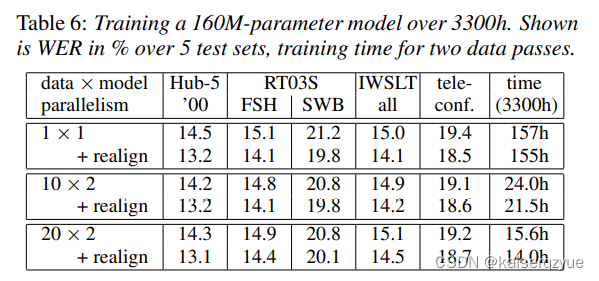
在这里插入图片描述