【算法题】最大矩形面积，单调栈解法

news2024/9/29 18:06:50

力扣：84. 柱状图中最大的矩形

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。
求在该柱状图中，能够勾勒出来的矩形的最大面积。
在这里插入图片描述

题意很简单，翻译一下就是：求该图中最大矩形的面积。

那么，这道题的思路就是遍历。不过如何高效遍历是一个学问。
这道题我带来单调栈的解法。

单调栈就是在栈中维护一个单调规律的序列。

这道题,我们可以维护一个单调递增的序列。
遇到该元素比栈顶元素小的情况，就把栈顶元素出栈，直到栈顶元素小于该元素，或该栈为空为止。
在这里插入图片描述

为什么要维护一个单调递增的序列呢？

由于序列是递增的所以，最大矩形会非长容易算出最大矩形的面积。
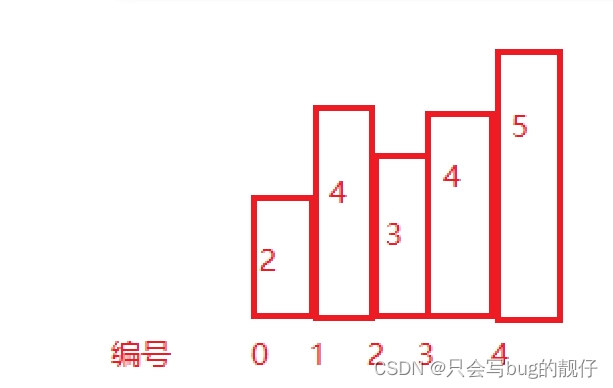
在这里插入图片描述
以该矩形为例
以2为高的最大矩形是 2 * 4 = 4；
以3为高的最大矩形是3 * 3 = 9；
以4为高的最大矩形是4 * 2 = 8；
以5为高的最大矩形是5 * 1 = 1；

那么有人要问了，有聪明的小脑管们要问了，哎呀。
实际上某些矩形中间还有矩形，并不是真正的递序列，会不会产生影响捏？
在这里插入图片描述

如果原图为这样，那么出栈之后维护的递增图与上图对应。由于中间的4大于3也大于2，所以，中间的矩形应该是最大的，可以把4当成3即可。我们可以以出栈为契机，计算矩形的面积
以该图我进行解题语言描述：
1：栈中为空栈，将矩形0入栈。此时栈中矩形为：0
2：矩形1的高为4，大于栈顶元素2，将矩形1入栈，此时栈中矩形为 0 ，1
3：矩形2的高为3，3小于栈顶元素的高4，所以将栈顶矩形1出栈，同时计算矩形1高的最大
矩形，为 4 * 1 = 4；同时将3入栈，此时栈中矩形为： 0， 2
4:因为矩形3的高大于栈顶矩形2的高，所以将矩形3入栈，此时栈中矩形为： 0， 2，3
5:因为矩形4的高大于栈顶矩形3的高，所以将矩形4入栈，此时栈中矩形为： 0， 2，3，4
6.此时所有的元素已经入栈完毕，且栈中元素为地址矩形，依次出栈计算所有值即可,最重要的出栈，即出栈到3的时候，不能直接拿4矩形序号减去2徐行序号 + 1，因为2号矩形前面可能还有徐行，应该捡到0矩形之后，2矩形之前。

JAVA代码的实现

class Solution {
    public int largestRectangleArea(int[] heights) {

       
        int maxS = 0;
        Stack<Integer> st = new Stack<>();
        //添加矩形入栈
        for(int i = 0; i < heights.length; i++){
            if(st.empty() || heights[i] >= heights[st.peek()]){
                st.push(i);
            }else{
                while(!st.empty() && heights[st.peek()] > heights[i]){

                        int tempH2 = heights[st.pop()];
                        if(st.empty()){
                            maxS = Math.max(tempH2 * i,maxS);
                            break;
                        }else {

                        }
                        maxS = Math.max(maxS, (i - st.peek() - 1) * tempH2);


                }
                st.push(i);
            }
        }
        //添加完毕，依次出栈
        if(!st.empty()){
            int tempH = heights[st.peek()];
            int tempI = st.pop();
            if (st.empty()){
                maxS = Math.max(maxS, tempH);
                return maxS;
            }else {
                maxS = Math.max(maxS, tempH * (tempI - st.peek()));
            }

            while(!st.empty()){
                int tempH2 = heights[st.pop()];
                if(st.empty()){
                    maxS = Math.max(tempH2 * (tempI + 1),maxS);
                    break;
                }
                maxS = Math.max(maxS, (tempI - st.peek()) * tempH2);
            }
        }
        return maxS;

    }
}

同时该题也有一种取巧的做法，在守卫补两个高度为0的矩形，不影响结果的情况下，可以将流程统计，即压入最右面的0的时候吧所有的矩形都出栈，所有矩形将出栈完毕，即计算完毕。
JAVA代码实现

	 public int largestRectangleArea(int[] heights) {
        int res =0 ;
        int n = heights.length;
        int[] arr = new int[n+2];
        //复制数组,首位加0
        System.arraycopy(heights,0,arr,1,n);
        Deque<Integer> stack = new ArrayDeque<>();
        int nOfArr = arr.length;

        arr[0] = arr[nOfArr-1] = 0;
        //依次比较入栈
        for (int i = 0; i < nOfArr; i++) {
            int h = arr[i];
            while (!stack.isEmpty() && h < arr[stack.peek()]){
                int tmph = arr[stack.pop()];
                res = Math.max(res,tmph * (i - stack.peek() - 1));
            }
            stack.push(i);
        }

        return res;
    }