周赛334（前缀和、贪心+双指针、Dijkstra求最短路径、二分答案）

文章目录

- [6369. 左右元素和的差值](https://leetcode.cn/problems/left-and-right-sum-differences/)
- - 前缀和
- [6368. 找出字符串的可整除数组](https://leetcode.cn/problems/find-the-divisibility-array-of-a-string/)
- - 超长整数如何取余？
- [6367. 求出最多标记下标](https://leetcode.cn/problems/find-the-maximum-number-of-marked-indices/)
- - 贪心 + 同向双指针
  - 二分答案
- [6366. 在网格图中访问一个格子的最少时间](https://leetcode.cn/problems/minimum-time-to-visit-a-cell-in-a-grid/)
- - Dijkstra求最短路径
  - 二分答案

6369. 左右元素和的差值

难度简单4

给你一个下标从 0 开始的整数数组 nums ，请你找出一个下标从 0 开始的整数数组 answer ，其中：

answer.length == nums.length
answer[i] = |leftSum[i] - rightSum[i]|

其中：

leftSum[i] 是数组 nums 中下标 i 左侧元素之和。如果不存在对应的元素，leftSum[i] = 0 。
rightSum[i] 是数组 nums 中下标 i 右侧元素之和。如果不存在对应的元素，rightSum[i] = 0 。

返回数组 answer 。

示例 1：

输入：nums = [10,4,8,3]
输出：[15,1,11,22]
解释：数组 leftSum 为 [0,10,14,22] 且数组 rightSum 为 [15,11,3,0] 。
数组 answer 为 [|0 - 15|,|10 - 11|,|14 - 3|,|22 - 0|] = [15,1,11,22] 。

示例 2：

输入：nums = [1]
输出：[0]
解释：数组 leftSum 为 [0] 且数组 rightSum 为 [0] 。
数组 answer 为 [|0 - 0|] = [0] 。

提示：

1 <= nums.length <= 1000
1 <= nums[i] <= 105

前缀和

class Solution {
    public int[] leftRigthDifference(int[] nums) {
        int n = nums.length;
        int[] leftsum = new int[n+1];
        int[] rightsum = new int[n+1];
        for(int i = 0; i < n; i++){
            leftsum[i+1] = leftsum[i] + nums[i];
        }
        for(int i = n-1; i > 0; i--){
            rightsum[i-1] = rightsum[i] + nums[i];
        }
        int[] res = new int[n];
        for(int i = 0; i < n; i++){
            res[i] = Math.abs(leftsum[i] - rightsum[i]);
        }
        return res;
    }
}

6368. 找出字符串的可整除数组

难度中等4

给你一个下标从 0 开始的字符串 word ，长度为 n ，由从 0 到 9 的数字组成。另给你一个正整数 m 。

word 的 可整除数组 div 是一个长度为 n 的整数数组，并满足：

如果 word[0,...,i] 所表示的数值能被 m 整除，div[i] = 1
否则，div[i] = 0

返回 word 的可整除数组。

示例 1：

输入：word = "998244353", m = 3
输出：[1,1,0,0,0,1,1,0,0]
解释：仅有 4 个前缀可以被 3 整除："9"、"99"、"998244" 和 "9982443" 。

示例 2：

输入：word = "1010", m = 10
输出：[0,1,0,1]
解释：仅有 2 个前缀可以被 10 整除："10" 和 "1010" 。

提示：

1 <= n <= 105
word.length == n
word 由数字 0 到 9 组成
1 <= m <= 109

超长整数如何取余？

class Solution {
    // 本质就是超级长的整数如何取余
    public int[] divisibilityArray(String word, int m) {
        double x = 0; // 第 i 位 用第 i-1 位 * 10 + word[1] 表示, 来防止溢出
        int n = word.length();
        int[] res = new int[n];
        for(int i = 0; i < n; i++){
            x = (x*10 + (word.charAt(i) - '0')) % m;
            res[i] = (x == 0) ? 1 : 0;
        }
        return res;
    }
}

6367. 求出最多标记下标

难度中等17

给你一个下标从 0 开始的整数数组 nums 。

一开始，所有下标都没有被标记。你可以执行以下操作任意次：

选择两个 互不相同且未标记 的下标 i 和 j ，满足 2 * nums[i] <= nums[j] ，标记下标 i 和 j 。

请你执行上述操作任意次，返回 nums 中最多可以标记的下标数目。

示例 1：

输入：nums = [3,5,2,4]
输出：2
解释：第一次操作中，选择 i = 2 和 j = 1 ，操作可以执行的原因是 2 * nums[2] <= nums[1] ，标记下标 2 和 1 。
没有其他更多可执行的操作，所以答案为 2 。

示例 2：

输入：nums = [9,2,5,4]
输出：4
解释：第一次操作中，选择 i = 3 和 j = 0 ，操作可以执行的原因是 2 * nums[3] <= nums[0] ，标记下标 3 和 0 。
第二次操作中，选择 i = 1 和 j = 2 ，操作可以执行的原因是 2 * nums[1] <= nums[2] ，标记下标 1 和 2 。
没有其他更多可执行的操作，所以答案为 4 。

示例 3：

输入：nums = [7,6,8]
输出：0
解释：没有任何可以执行的操作，所以答案为 0 。

提示：

1 <= nums.length <= 105
1 <= nums[i] <= 109

贪心 + 同向双指针

class Solution {
    // 2 3 4 5
    public int maxNumOfMarkedIndices(int[] nums) {
        Arrays.sort(nums);
        int res = 0;
        int n = nums.length;
        int left = 0, right = n / 2;
        while(left < n/2 && right < n){
            if(nums[left] * 2 <= nums[right]){
                res += 2;
                left++;
                right++;
            }else{
                right++;
            }
        }
        return res;
    }
}

二分答案

class Solution {
    /**
        二分答案：考虑匹配k对
        如果能匹配k对，则一定能匹配k-1对、k-2对...
     */
    public int maxNumOfMarkedIndices(int[] nums) {
        Arrays.sort(nums);
        int left = 0, right = nums.length/2;
        while(left <= right){
            int mid = (left + right) >> 1;
            if(check(nums, mid)){
                left = mid+1;
            }else{
                right = mid-1;
            }
        }
        return right * 2;
    }

    public boolean check(int[] nums, int k){
        for(int i = 0; i < k; i++){
            if(nums[i] * 2 > nums[nums.length-k+i])
                return false;
        }
        return true;
    }
}

6366. 在网格图中访问一个格子的最少时间

难度困难15

给你一个 m x n 的矩阵 grid ，每个元素都为非负整数，其中 grid[row][col] 表示可以访问格子 (row, col) 的最早时间。也就是说当你访问格子 (row, col) 时，最少已经经过的时间为 grid[row][col] 。

你从 最左上角 出发，出发时刻为 0 ，你必须一直移动到上下左右相邻四个格子中的任意一个格子（即不能停留在格子上）。每次移动都需要花费 1 单位时间。

请你返回最早到达右下角格子的时间，如果你无法到达右下角的格子，请你返回 -1 。

示例 1：

输入：grid = [[0,1,3,2],[5,1,2,5],[4,3,8,6]]
输出：7
解释：一条可行的路径为：
- 时刻 t = 0 ，我们在格子 (0,0) 。
- 时刻 t = 1 ，我们移动到格子 (0,1) ，可以移动的原因是 grid[0][1] <= 1 。
- 时刻 t = 2 ，我们移动到格子 (1,1) ，可以移动的原因是 grid[1][1] <= 2 。
- 时刻 t = 3 ，我们移动到格子 (1,2) ，可以移动的原因是 grid[1][2] <= 3 。
- 时刻 t = 4 ，我们移动到格子 (1,1) ，可以移动的原因是 grid[1][1] <= 4 。
- 时刻 t = 5 ，我们移动到格子 (1,2) ，可以移动的原因是 grid[1][2] <= 5 。
- 时刻 t = 6 ，我们移动到格子 (1,3) ，可以移动的原因是 grid[1][3] <= 6 。
- 时刻 t = 7 ，我们移动到格子 (2,3) ，可以移动的原因是 grid[2][3] <= 7 。
最终到达时刻为 7 。这是最早可以到达的时间。

示例 2：

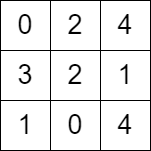
输入：grid = [[0,2,4],[3,2,1],[1,0,4]]
输出：-1
解释：没法从左上角按题目规定走到右下角。

提示：

m == grid.length
n == grid[i].length
2 <= m, n <= 1000
4 <= m * n <= 105
0 <= grid[i][j] <= 105
grid[0][0] == 0

Dijkstra求最短路径

题解：https://leetcode.cn/problems/minimum-time-to-visit-a-cell-in-a-grid/solution/er-fen-da-an-bfspythonjavacgo-by-endless-j10w/

class Solution {
    private final static int[][] dirs = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};

    public int minimumTime(int[][] grid) {
        int m = grid.length, n = grid[0].length;
        if(grid[0][1] > 1 && grid[1][0] > 1) return -1;
        // 否则答案一定存在（因为可以反复横跳来拖延时间）
        // 到达grid[i][j] 的最小时间 dis[i][j] 一定是和 (i+j) 同奇偶的
        // 如果到达时不同奇偶， 则+1就行
        int[][] dis = new int[m][n];
        for(int i = 0; i < m; i++){
            Arrays.fill(dis[i], Integer.MAX_VALUE);
        }
        dis[0][0] = 0;
        PriorityQueue<int[]> pq = new PriorityQueue<>((a,b) -> a[0]-b[0]);
        pq.add(new int[]{0,0,0});
        while(true){
            int[] poll = pq.poll();
            int d = poll[0], i = poll[1], j = poll[2];
            if(i == m-1 && j == n-1) return d;
            for(int[] dir : dirs){ // 枚举周围四个格子
                int x = i + dir[0], y = j + dir[1];
                if(x >= 0 && x < m && y >= 0 && y < n){
                    int nd = Math.max(d+1, grid[x][y]);
                    nd += (nd-x-y) % 2; // nd 必须和 x+y 同奇偶
                    if(nd < dis[x][y]){
                        dis[x][y] = nd; // 更新最短路
                        pq.add(new int[]{nd, x, y});
                    }
                }
            }
        }
    }
}

二分答案

二分到终点的时间，然后跑 BFS

如果可以从终点到达起点，说明可以在大于 endTime 的时刻到达终点；反之，如果无法从终点到达起点，说明无法在小于 endTime 的时刻到达终点。

有单调性，可以二分到达终点的时间。

class Solution {
    private final static int[][] dirs = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
    private int[][] grid, vis;

    public int minimumTime(int[][] grid) {
        int m = grid.length, n = grid[0].length;
        if (grid[0][1] > 1 && grid[1][0] > 1) // 无法「等待」
            return -1;

        this.grid = grid;
        vis = new int[m][n];
        int left = Math.max(grid[m - 1][n - 1], m + n - 2) - 1;
        int right = (int) 1e5 + m + n; // 开区间
        while (left + 1 < right) {
            int mid = (left + right) >>> 1;
            if (check(mid)) right = mid;
            else left = mid;
        }
        return right + (right + m + n) % 2;
    }

    private boolean check(int endTime) {
        int m = grid.length, n = grid[0].length;
        vis[m - 1][n - 1] = endTime;
        var q = new ArrayList<int[]>();
        q.add(new int[]{m - 1, n - 1});
        for (int t = endTime - 1; !q.isEmpty(); --t) {
            var tmp = q;
            q = new ArrayList<>();
            for (var p : tmp) {
                int i = p[0], j = p[1];
                for (var d : dirs) { // 枚举周围四个格子
                    int x = i + d[0], y = j + d[1];
                    if (0 <= x && x < m && 0 <= y && y < n && vis[x][y] != endTime && grid[x][y] <= t) {
                        if (x == 0 && y == 0) return true;
                        vis[x][y] = endTime; // 用二分的值来标记，避免重复创建 vis 数组
                        q.add(new int[]{x, y});
                    }
                }
            }
        }
        return false;
    }
}

 if (0 <= x && x < m && 0 <= y && y < n && vis[x][y] != endTime && grid[x][y] <= t) {
                    if (x == 0 && y == 0) return true;
                    vis[x][y] = endTime; // 用二分的值来标记，避免重复创建 vis 数组
                    q.add(new int[]{x, y});
                }
            }
        }
    }
    return false;
}

}