正态性检验处理流程

一、分析问题
在实际研究中,正态性是很多研究方法在进行分析时需要满足的前提条件。常见的比如方差分析、T检验、相关分析、回归分析等等,这些分析方法使用的前提假定就是需要数据满足正态分布。
但是这一点经常被分析人员有意或无意的忽略掉。原因一可能在于大家“心照不宣”的默认数据满足正态性;原因二可能是分析人员的数据分析基础知识不够,不知道需要进行正态性检验;原因三可能在于知道数据需要满足正态分布,但是数据无论如何都无法满足正态性,就放弃了。
如果说数据分析方法没有满足需要的前提条件,那么分析得到的结果就是不够科学、不够严谨的,甚至得到的分析结论也会“本末倒置”。这就提示我们数据分析一定要严谨,正态性检验必不可少,接下来将介绍一下正态性检验方式。
二、检验方式
正态性检验方式主要有统计检验法、描述法、图示法这三大类。
当前有3个班级90名同学的期中考试成绩,现在要检验成绩是否满足正态分布,部分数据如下:
我们将分别使用这三类分析方法进行正态性检验,这三类方法都可以在SPSSAU系统找到,下面将一一进行介绍说明。
- 统计检验法
统计检验法是检验正态性的最严格方法,对数据要求最为严格。统计检验法包括两种检验方式,分别是Kolmogorov-Smirnov检验和Shapiro-Wilk检验。如果样本量大于50,则使用K-S检验(Kolmogorov-Smirnov检验),反之则使用S-W检验(Shapiro-Wilk检验)。
SPSSAU正态性检验分析结果如下:

因为样本量为90,大于50,所以使用K-S检验进行,具体来看,成绩全部均没有呈现显著性(p>0.05),所以成绩全部具有正态性特质,满足正态分布。
- 描述法
统计检验法一般来讲是很难满足的,所以在正态性检验分析结果中,还可以看峰度和偏度两个指标,描述法是使用峰度和偏度考察数据的正态性。一般认为,如果峰度绝对值小于10并且偏度绝对值小于3,则说明数据虽然不是绝对正态,但基本可接受为正态分布。

从上图通过查看偏度和峰度,也可以得到数据满足正态分布的性质。
- 图示法
大部分情况下,如果对数据要求不是特别严格,一般使用图示法进行数据的正态性检验。图示法包括查看数据直方图、P-P图和Q-Q图三种。
3.1 直方图
如果直方图的形状近似满足“中间高,两头低”的钟形分布,则说明数据近似满足正态分布特性,不必过多纠结数据的正态性。
SPSSAU直方图输出结果如下:
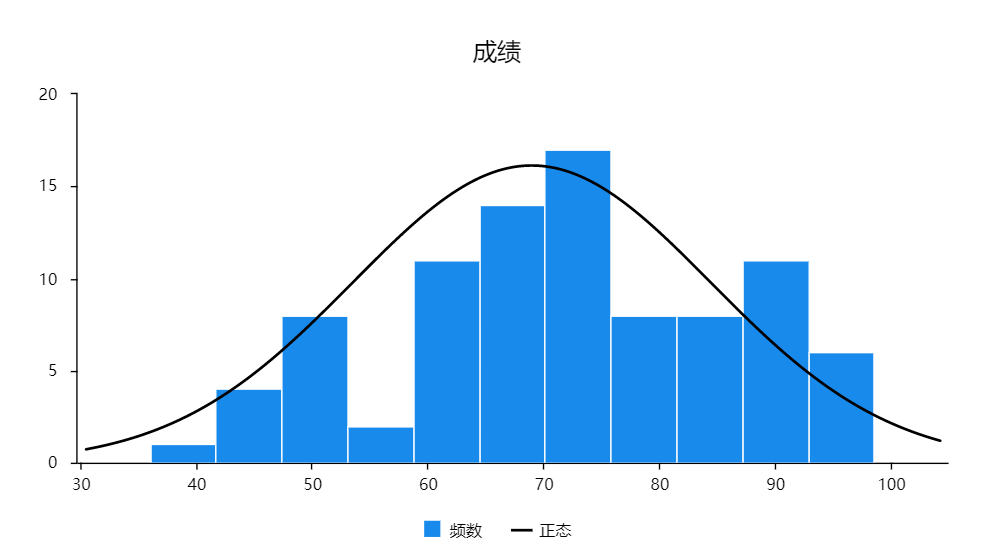
从上图可以看出,成绩的直方图基本满足“中间高,两头低”的钟形分布,说明数据满足正态分布特性。
3.2 P-P图
P-P图其原理在于如果数据正态,那么数据的累积比例与正态分布累积比例基本保持一致。分别计算出数据累积比例,和假定正态时的数据分布累积比例;并且将实际数据累积比例作为X轴,将对应正态分布累积比例作为Y轴,作散点图。
SPSSAU的P-P图输出结果如下:

从P-P图可以看出,散点图近似呈现一条对角直线,说明成绩呈现正态分布。
3.3 Q-Q图
Q-Q图其原理在于如果数据正态,那么其假定的正态分位数会与实际数据基本一致。计算出假定正态时的数据分位数;并且将实际数据作为X轴,将假定正态时的数据分位数作为Y轴,作散点图。
SPSSAU的Q-Q图输出结果如下:
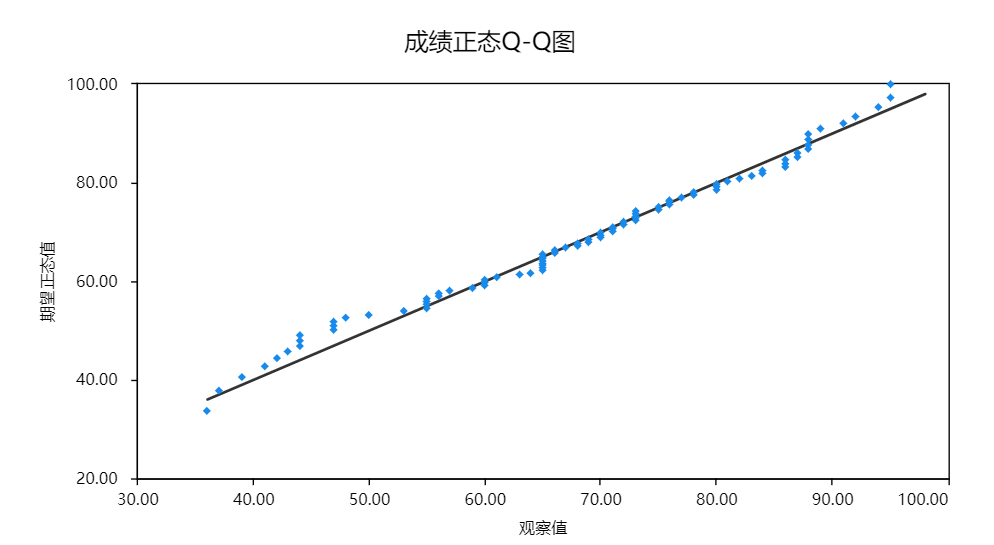
从Q-Q图可以看出,散点图近似呈现一条对角直线,说明成绩呈现正态分布。
三、非正态转化
从理论上讲,很多研究方法需要满足正态分布特质,但现实情况下,很难满足正态分布性。这样就需要进行非正态转化,想办法将不满足正态性特性的数据,经过一些方法,转化为满足正态分布的数据。非正态转化为正态数据的常见方法有以下几种:
- 取对数
a'=log(a)将原始数据a的对数值作为新的数据再进行分析;当原始数据中含有0或者负数时,可以根据内容自主进行相应改动:如 a'=log(a+x)。 - 开根号
a'=sqrt(a)将原始数据a的平方根作为新的数据再进行分析;同样的,如果a为0,可以将a加上一个合适的值进行变换。 - 取倒数
a'=1/a将原始数据a的倒数值作为新的数据再进行分析。 - 移除异常值
异常值,也称离群值,是指样本中的个别值,其数值明显偏离所属样本的绝大部分观测值。不论进行什么分析,如果数据中存在异常值,都应该在分析前进行处理,否则很可能影响分析结果,甚至扭曲结论。异常值可在SPSSAU->数据处理->异常值中进行处理。 - BOX-COX转换
针对数据进行Box-Cox变换,尽量让数据满足正态性。
例如现在有一份数据,在进行正态性检验时,p值为0.019<0.05,说明数据不具有正态性特质。将数据进行BOX-COX转换后,二者进行正态性检验得到分析结果如下表:

从上表可以看出,虽然再经过BOX-COX转换后p值仍小于0.05,没有通过正态性检验,但p值从0.019变为0.042,明显接近0.05,说明BOX-COX转换对于正态性的改善是有作用的。
- Johnson转换
同样的,Johnson转换与BOX-COX转换一样,都是通过某种变换使得数据尽量满足正态性。

从上表可以明显看出,虽然再经过Johnson转换后p值仍小于0.05,没有通过正态性检验,但p值从0.019变为0.042,明显接近0.05,说明Johnson转换对于正态性的改善是有作用的。
- 加大样本量
一般认为,有可能随着样本数增加越倾向于拒绝原假设(服从正态分布)。即样本数据量越大,则可以认为数据越具有正态性特质。所以可以通过加大样本量的方法提高数据的正态性。但这种方法在实际情况中很难实现,因为数据一般都是已经收集完成再进行分析的,此时再去收集数据加大样本量并不现实。
四、正态转化优劣对比
并不是所有数据在进行以上非正态转化后都可以呈现出正态性特征的。如果在进行非正态转化后数据仍不满足正态性,此时说明数据并不适合使用方差分析、t检验等方法,可以选择其他方法进行分析。举例说明如下图:
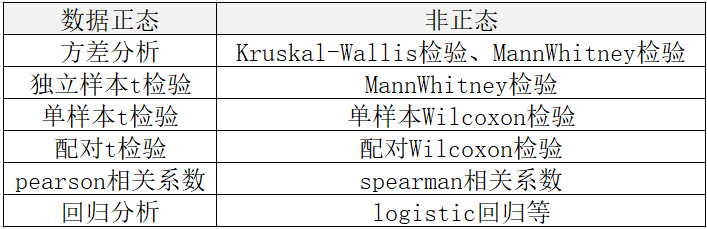
五、总结
在实际研究中,很多分析方法的前提条件都要求数据满足正态性特征,所以在分析前需要进行正态性检验。正态性检验的方法包括统计检验法、描述法、图示法三大类。其中,统计检验法对于数据正态性要求最为严格,绝对正态数据一般很难达到。一般使用描述法或图示法进行检验,数据近似满足正态性特征即可。如果经过检验发现数据并不满足正态性特征,这个时候可以先进行数据的非正态转化,但是转化并不能保证数据一定能满足正态性特征。同时需要注意,有实际意义的数据经过转化后可能失去实际意义。如果无论如何数据都不能满足正态性,此时可以考虑使用非参数检验等方法进行分析。