KMP算法的原理：

KMP算法：解决字符串匹配的问题。

前缀：包含首字母不包含尾字母的所有子串。

后缀：包含尾字母不包含首字母的所有子串。

最长相等前后缀：以模式串aabaaf为例，这里从a开始到aabaaf，可以知道aabaa为最长相等前后缀---长度为2。

next数组：放前缀表，以aabaaf为例对应的就是010120。遇到冲突时，核心用于向前回退。

一、实现strStr()

题目描述：

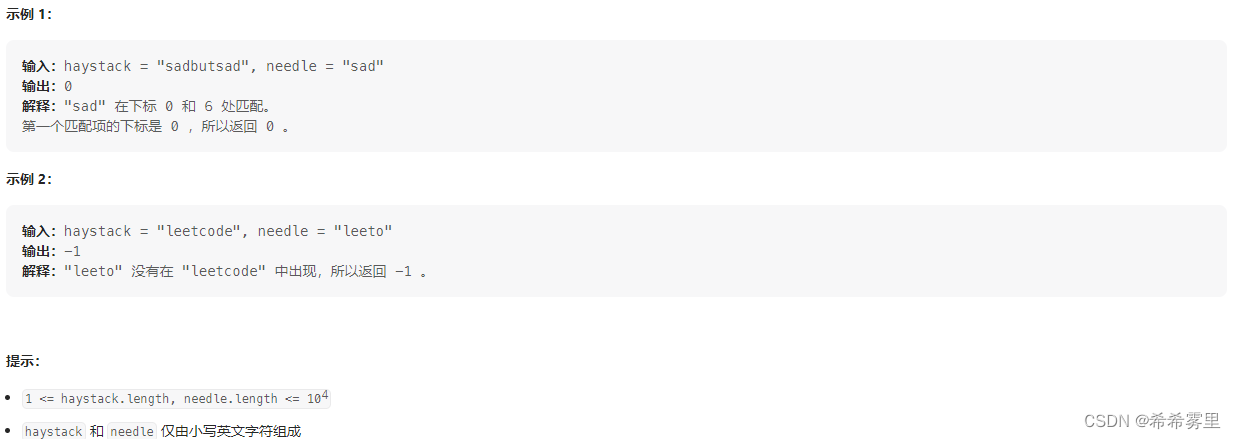
给你两个字符串 haystack 和 needle ，请你在 haystack 字符串中找出 needle 字符串的第一个匹配项的下标（下标从 0 开始）。如果 needle 不是 haystack 的一部分，则返回  -1 。

思路和想法：

         这里是字符串匹配问题，采用KMP算法，第一步获得next数组，第二步应用next数组获得第一个匹配的下标。

• 获取next数组：里面有四个步骤        ①初始化 i后缀末尾 j前缀末尾         ②前后缀不相同时，对i和j的处理        ③   前后缀相同时，对j的处理        ④对next数组的更新

    void getNext(int* next, const string& s){
        //步骤一
        int j = 0;
        next[0] = 0;
        for(int i = 1; i < s.size(); i++){
            //步骤二
            while(j > 0 && s[i] != s[j]){
                j = next[j - 1];
            }
            //步骤三
            if(s[i] == s[j]){
                j++;
            }
            //步骤四
            next[i] = j;
        }
    }

• 获取第一个匹配的下标

int strStr(string haystack, string needle) {
        if(needle.size() == 0) return 0;
        int next[needle.size()];
        getNext(next, needle);
        int j = 0;
        for (int i = 0; i < haystack.size(); i++) {
            while(j > 0 && haystack[i] != needle[j]) {
                j = next[j - 1];
            }
            if (haystack[i] == needle[j]) {
                j++;
            }
            if (j == needle.size() ) {
                return (i - needle.size() + 1);
            }
        }
        return -1;
    }

二、重复的子字符串

题目描述：

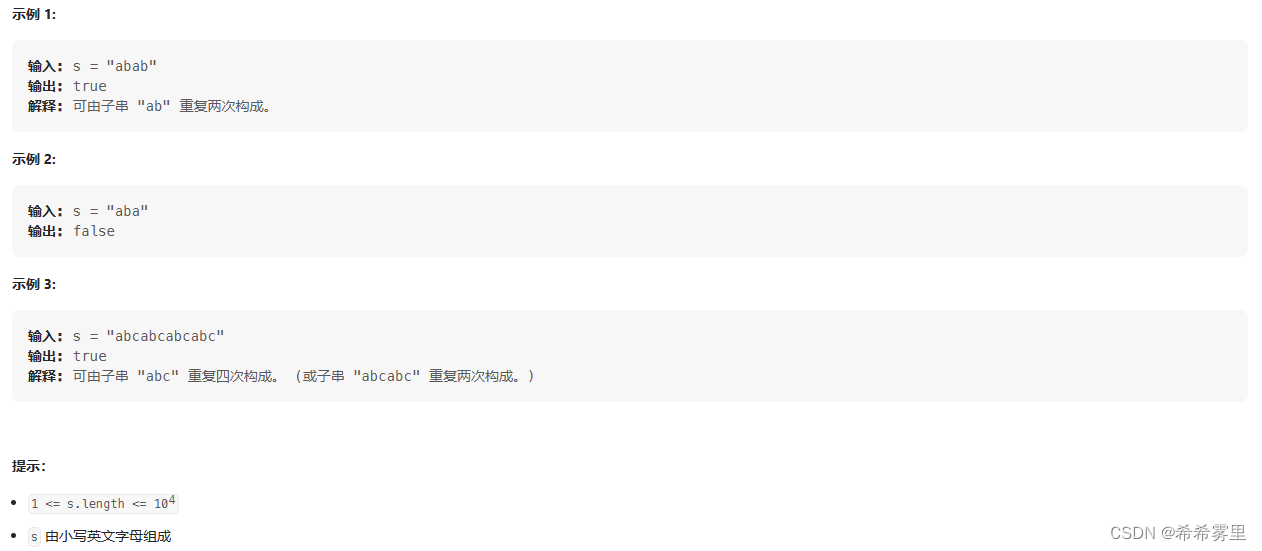
给定一个非空的字符串 s ，检查是否可以通过由它的一个子串重复多次构成。

思路和想法：

         这里可以采用KMP算法来解决。KMP算法擅长在一个串中查找是否出现过另一个串，这里判断是否有重复的子字符串与KMP算法之间的关联。        

        它们之间的联系，判断是否有的条件就是：next数组长度减去最长相同前后缀的长度相当于是第一个周期的长度，也就是一个周期的长度，如果这个周期可以被整除，就说明整个数组就是这个周期的循环。

    bool repeatedSubstringPattern(string s) {
        if (s.size() == 0) {
            return false;
        }
        int next[s.size()];
        getNext(next, s);
        int len = s.size();
        if (next[len - 1] != 0 && len % (len - (next[len - 1] )) == 0) {
            return true;
        }
        return false;
    }

完整代码如下：

class Solution {
public:
    void getNext(int* next, const string& s){
        int j = 0;
        next[0] = 0;
        for(int i = 1; i < s.size(); i++){
            while(j > 0 && s[i] != s[j]){
                j = next[j - 1];
            }
            if(s[i] == s[j]){
                j++;
            }
            next[i] = j;
        }
    }
    bool repeatedSubstringPattern(string s) {
        if (s.size() == 0) {
            return false;
        }
        int next[s.size()];
        getNext(next, s);
        int len = s.size();
        if (next[len - 1] != 0 && len % (len - (next[len - 1] )) == 0) {
            return true;
        }
        return false;
    }
};