案例引入

以下则是各个字符串经过括号处理之后的结果：

12((21))(12-->12(21)12
32((((2121)212(21)-->32(2121)212(21)
ABDF((SA)SA)SA(SA)SA(((-->ABDF((SA)SA)SA(SA)SA

算法思路：

这个问题的解决方法就是将字符按顺序逐一加入到新的string容器store中，当遇到'('或')'时需要对字符的加入方式做特殊处理。

定义处理该多余括号字符串的函数为 string removeParentheses（string& s,int& i）; 定义中途辅助函数为string sonSolution(string& s,int& i).

为了简化问题求解，只讨论第一个所遇到的括号字符。因此，对于字符的处理可以分为三种情况：

第一种，非括号字符直接加入到新容器store中；

第二种，当我们遇到的第一个括号')'时，由于')'前面没有与之匹配的'(',因此这个')'不能加入到新容器，直接舍去。对于该')'后面的字符串，由于其加入方式不受前面加入字符的影响，因此可以递归调用本函数，将递归返回值，即后续待被处理的子串接在store后面。(递归体现) 如图所示：

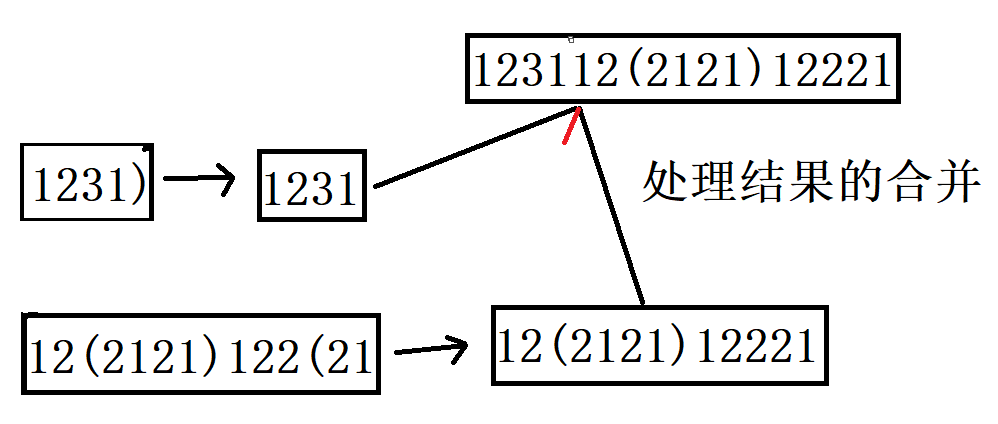
第三种，当遇到的第一个括号为'('时，需要对后续的字符加入方式做特殊处理。（在此我们需要再定义一个函数）

在第三种情况里面，函数所处理的字符依旧分为三种情况：

第一种，后续字符为非括号字符，直接加入到新容器newstore里面；

第二种，当遇到的第一个括号字符为')'时，直接加入到store中，并break返回结果。

第三种，若所遇到的弟也给括号字符为'('时，递归调用该函数(递归体现)。

以上就是如何删除多余括号的处理方式，同时需要借用下标i记录字符当前的读取位置，并且i==s.size()为读取结束标志。

代码实现

口说无凭，以下是代码实现：

#include<iostream>
using namespace std;
#include<string>
class solution {
public:
    string sonSolution(string& s, int& i) {
        i++;
        string newstore = "";
        while (i != s.size()) {
            if (s[i] == ')') {
                newstore = '(' + newstore + ')';
                i++;
                break;
            }
            else if (s[i] == '(') {
                newstore += sonSolution(s, i);
            }
            else {
                newstore += s[i];
                i++;
            }
        }
        return newstore;
    }
    string removeParentheses(string& s, int& i) {
        string store = "";
        while (i != s.size()) {
            if (s[i] == ')') {
                i++;
                store += removeParentheses(s, i);
            }
            else if (s[i] == '(') {
                store+=sonSolution(s, i);
            }
            else {
                store += s[i];
                i++;
            }
        }
        return store;
    }
};

int main() {
    solution s;
    for (int j = 0;j < 3;j++) {
        int i = 0;
        cout << "原始字符串:" << endl;
        string str;
        cin >> str;
        cout << "处理结果:" << endl;
        cout << s.removeParentheses(str, i) << endl;
    }
    return 0;
}

测试结果：

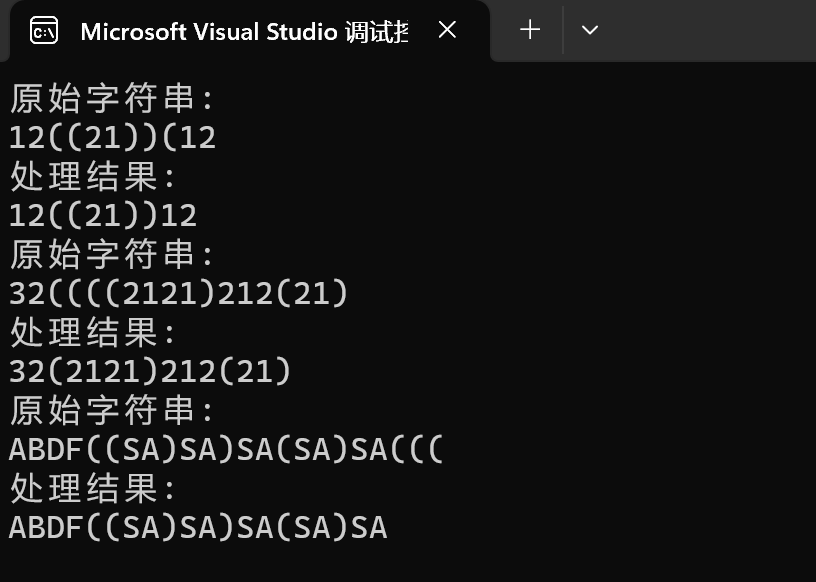
结语

该问题不只有一种解法，利用栈的数据结构也能解决问题，但总体思路是，'('只有遇到')'才能完成匹配，否则需要舍弃，在'('加入到新容器前可以先搜索它后面的括号情况，再根据情况做出判断；当只有遇到')'时，由于没有与'('直接舍弃，否则与')'构成完整的字符串作为返回值。期间对于已经完成匹配括号的子串，其后面剩余的字符串可以递归处理，以简化问题求解。