详解C语言实现二叉树~😎
- 前言🙌
- 什么是二叉树?
- 二叉树的性质总结:
- 整体实现内容分析💞
- 1.头文件的编写:🙌
- 2.功能文件的编写:🙌
- 1)前序遍历的数值来创建树——递归函数实现 😊
- 2)求树的高度函数实现 😊
- 3)求叶子数函数实现 😊
- 4)求树的总结点个数函数实现 😊
- 5)前序遍历二叉树实现 😊
- 6)中序遍历二叉树实现 😊
- 7)后序遍历二叉树实现 😊
- 8)删除二叉树函数实现 😊
- 3.测试文件编写::🙌
- 总结撒花💞

😎博客昵称:博客小梦
😊最喜欢的座右铭:全神贯注的上吧!!!
😊作者简介:一名热爱C/C++,算法等技术、喜爱运动、热爱K歌、敢于追梦的小博主!
😘博主小留言:哈喽!😄各位CSDN的uu们,我是你的博客好友小梦,希望我的文章可以给您带来一定的帮助,话不多说,文章推上!欢迎大家在评论区唠嗑指正,觉得好的话别忘了一键三连哦!😘
前言🙌
哈喽各位友友们😊,我今天又学到了很多有趣的知识,现在迫不及待的想和大家分享一下!😘我仅已此文,手把手带领大家详解C语言实现二叉树~ 利用二叉链式存储结构来完成二叉树的实现,并完成叶子高度,前序遍历生成树,叶节点的个数,结点总数,前序遍历,中序遍历,后序遍历,销毁树。都是精华内容,可不要错过哟!!!😍😍😍
什么是二叉树?
满足以下两个条件的树就是二叉树:
- 本身是有序树;
- 树中包含的各个节点的度不能超过 2,即只能是 0、1 或者 2;
二叉树的性质总结:
- 二叉树中,第 i 层最多有 2^( i-1)个结点。
- 如果二叉树的深度为 K,那么此二叉树最多有 2^K-1 个结点。
- 二叉树中,终端结点数(叶子结点数)为 n0,度为 2 的结点数为 n2,则 n0=n2+1。
二叉树又可以分类为许多不同的二叉树:

整体实现内容分析💞
- 利用二叉链式存储结构来完成二叉树的实现,并完成叶子高度,前序遍历生成树,叶节点的个数,结点总数,前序遍历,中序遍历,后序遍历,销毁树。
- 采用递归的思想,先是malloc开辟结点空间,然后给结点赋值,然后递归左子树然后递归右子树。这里用*表示空。最后返回生成的root指针的地址求高度,采用后序遍历的思想。
- 相当于求左右子树结点高度的最大值。每次递归加1就是计算结点数。求叶子总数时先求出左子树的叶子数再加上右子树的叶子数。求总结点数时这里直接递归计算出左子树和右子树的总结点数,每次加1表示遍历的节点数计算。然后就是前中后序的实现,这里也是用到递归的思想,最后便是将数销毁掉,malloc生成的空间要用free手动销毁。
1.头文件的编写:🙌
头文件的编写的整体思路分析:
这里用的是二叉链式存储的实现。首先是定义结构体,然后是对求叶子高度,前序遍历生成树,叶节点的个数,结点总数,前序遍历,中序遍历,后序遍历,销毁树。
#pragma once
#include"stdio.h"
#include"stdlib.h"
typedef int datatype;
typedef struct node
{
datatype data;
struct node* lchild, * rchild;
}tree;
tree* Creatbitree();
int Depthbitree(tree* T);
int Leaf_count(tree* T);
int Countbitree(tree* T);
int Preorder(tree* T);
int Inorder(tree* T);
int Postorder(tree* T);
tree* Delete(tree* T);
2.功能文件的编写:🙌
1)前序遍历的数值来创建树——递归函数实现 😊
编写的整体思路分析:
采用递归的思想,先是malloc开辟结点空间,然后给结点赋值,然后递归左子树然后递归右子树。这里用*表示空。最后返回生成的root指针的地址
#include"BinaryTree.h"
tree* Creatbitree()//前序遍历的数值来创建树——递归
{
char ch;
tree* root;
scanf("%c", &ch);//用于接收输入的数值
if (ch == '*') return NULL;//用*来判断是否为空
else {
root = (tree*)malloc(sizeof(tree));
root->data = ch;//赋值
root->lchild = Creatbitree();//左子树
root->rchild = Creatbitree();//右子树
}
return root;
}
2)求树的高度函数实现 😊
编写的整体思路分析:
这里求高度,采用后序遍历的思想。相当于求左右子树结点高度的最大值。每次递归加1 就是计算结点数。
int Depthbitree(tree* T)//测量树的深度
{
if (T == NULL) return 0;
else {
int leftheighter = Depthbitree(T->lchild);
int rightheighter = Depthbitree(T->rchild);
return (leftheighter > rightheighter ? leftheighter + 1 : rightheighter + 1);
}
}
3)求叶子数函数实现 😊
编写的整体思路分析:
代码上已表明算法思想,先求出左子树的叶子数再加上右子树的叶子数。
int Leaf_count(tree* T)//测量叶子的数量
{
if (T == NULL) return 0;
else if (!T->lchild && !T->rchild)//如果左右结点都为空则他就是叶子结点
return 1;
else return Leaf_count(T->lchild) + Leaf_count(T->rchild);
}
4)求树的总结点个数函数实现 😊
编写的整体思路分析:
这里直接递归计算出左子树和右子树的总结点数,每次加1表示遍历的节点数计算。
int Countbitree(tree* T) //测量总的结点个数
{
if (T == NULL)
return 0;
else {
return Countbitree(T->lchild) + Countbitree(T->rchild)+1;
}
}
5)前序遍历二叉树实现 😊
int Preorder(tree* T)//前序遍历序列 (根左右)
{
if (T == NULL)
return 0;
else {
printf("%c ", T->data);//先输出根节点
Preorder(T->lchild);
Preorder(T->rchild);
}
}
6)中序遍历二叉树实现 😊
int Inorder(tree* T)//中序遍历序列 (左根右)
{
if (T == NULL)
return 0;
else {
Inorder(T->lchild);//先输出左孩子
printf("%c ", T->data);
Inorder(T->rchild);
}
}
7)后序遍历二叉树实现 😊
int Postorder(tree* T)//后序遍历序列 (左右根)
{
if (T == NULL)
return 0;
else {
Postorder(T->lchild);//先输出左孩子
Postorder(T->rchild);
printf("%c ", T->data);
}
}
8)删除二叉树函数实现 😊
tree* Delete(tree* T)//删除树
{
if (T->lchild)
Delete(T->lchild);
else if (T->rchild)
Delete(T->rchild);
else
free(T);
}
3.测试文件编写::🙌
#define _CRT_SECURE_NO_WARNINGS 1
#include"BinaryTree.h"
main()
{
tree* T;
T = (tree*)malloc(sizeof(tree));
T->lchild = NULL;
T->rchild = NULL;
printf("请输入树的前序遍历序列\n");
T = Creatbitree();
int n = Depthbitree(T);
int m = Leaf_count(T);
int l = Countbitree(T);
printf("树创建完成\n");
printf("前序输出为\n");
printf("\t\t");
Preorder(T);
printf("\n中序输出为\n");
printf("\t\t");
Inorder(T);
printf("\n后序输出为\n");
printf("\t\t");
Postorder(T);
printf("\n高度%d\n叶子%d\n总结点%d\n", n, m, l);
Delete(T);
printf("删除成功");
}
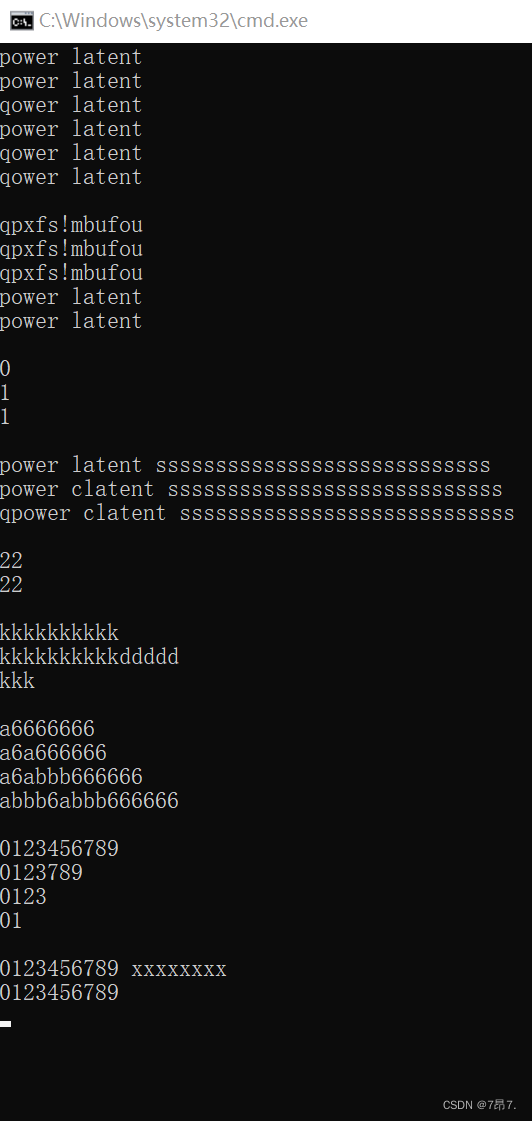
功能测试结果展示图:

总结撒花💞
本篇文章旨在分享详解C语言实现二叉树。希望大家通过阅读此文有所收获!本次主要是对二叉树的实现,这里只要用到的思想是递归,这也是难点所在。这就要需要画图帮忙辅助理解,递归的具体每一步是如何执行的需要分析清楚。在创建树的时候可以采用前序遍历思想创建,这种思想创建是比较好理解的,也可以用其他思想创建,相对比较难理解一点。以及区分好前中后序遍历的思想,然后再编写代码。
😘如果我写的有什么不好之处,请在文章下方给出你宝贵的意见😊。如果觉得我写的好的话请点个赞赞和关注哦~😘😘😘