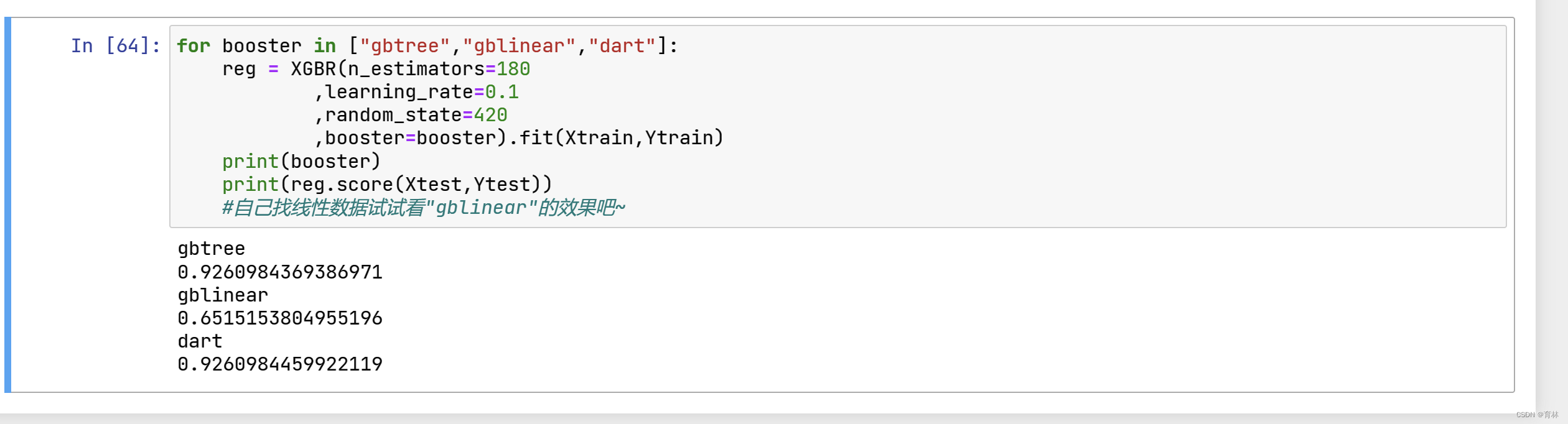
一、选择弱评估器：重要参数booster

class xgboost.XGBRegressor (kwargs，max_depth=3, learning_rate=0.1, n_estimators=100, silent=True,
objective=‘reg:linear’, booster=‘gbtree’, n_jobs=1, nthread=None, gamma=0, min_child_weight=1,
max_delta_step=0, subsample=1, colsample_bytree=1, colsample_bylevel=1, reg_alpha=0, reg_lambda=1,
scale_pos_weight=1, base_score=0.5, random_state=0, seed=None, missing=None, importance_type=‘gain’)

二、XGB的目标函数：重要参数objective

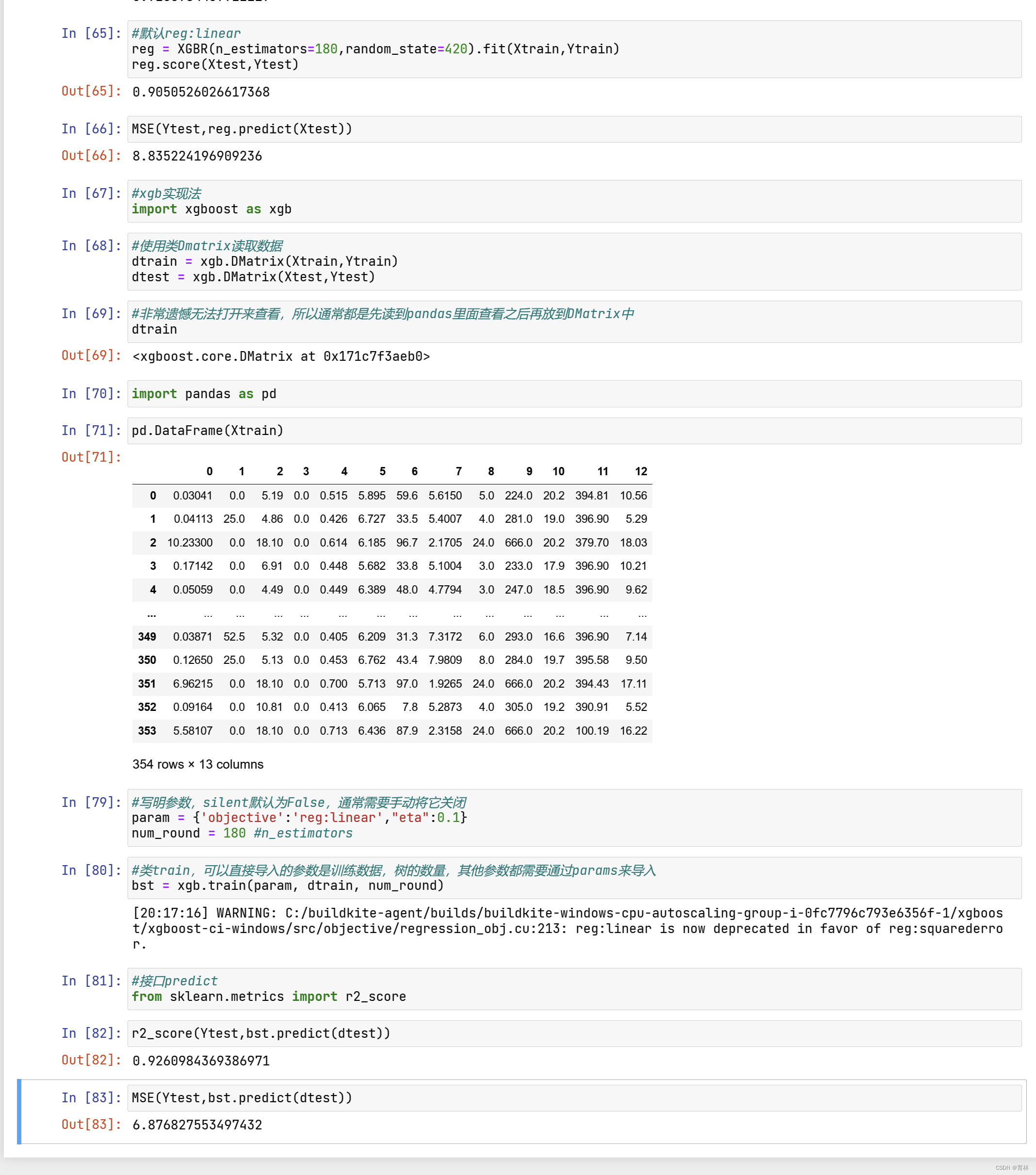
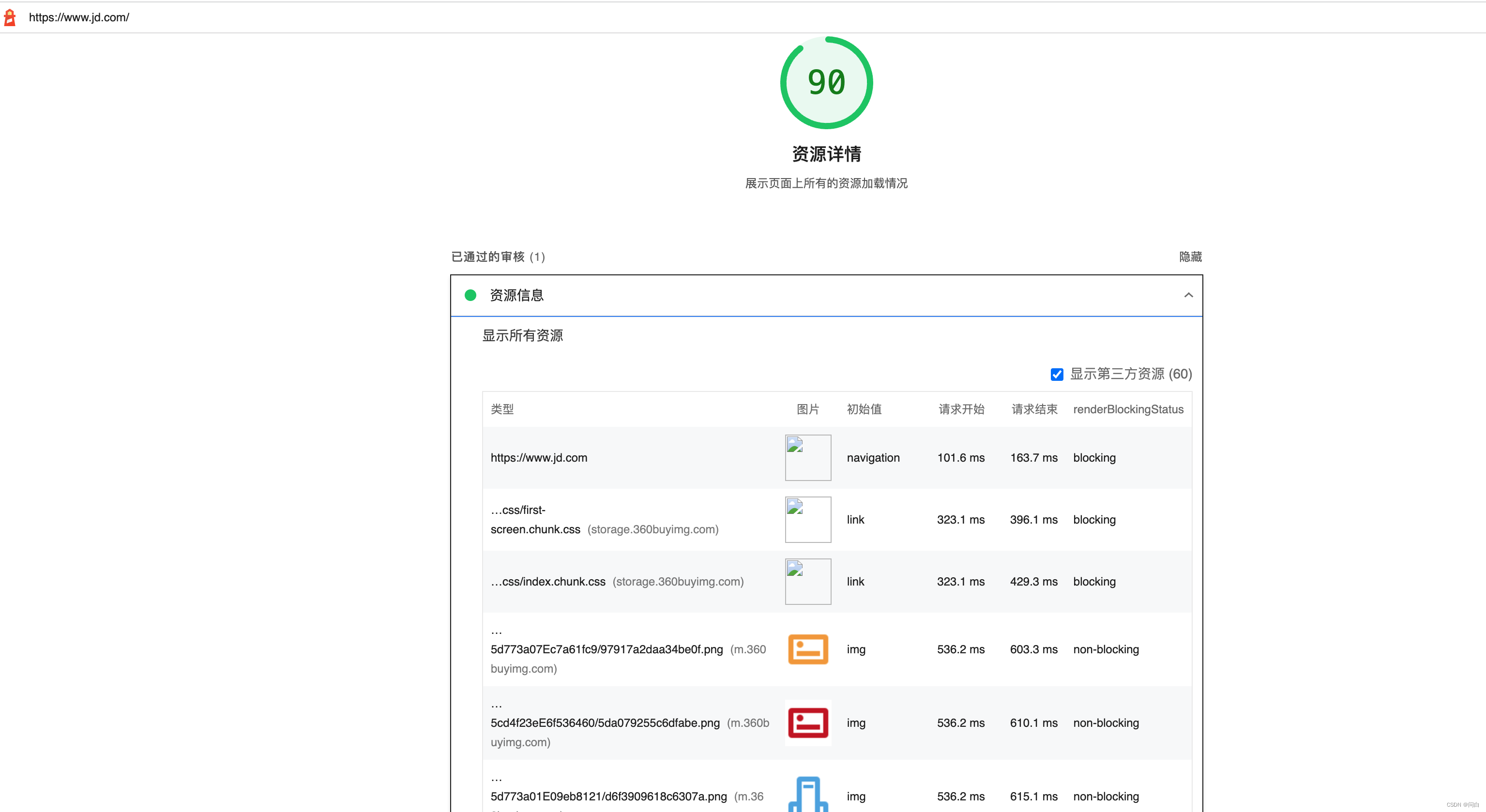
看得出来，无论是从R平方 还是从MSE的角度来看，都是xgb库本身表现更优秀，这也许是由于底层的代码是由不同团队
创造的缘故。随着样本量的逐渐上升，sklearnAPI中调用的结果与xgboost中直接训练的结果会比较相似，如果希望
的话可以分别训练，然后选取泛化误差较小的库。如果可以的话，建议脱离sklearnAPI直接调用xgboost库，因为
xgboost库本身的调参要方便许多。

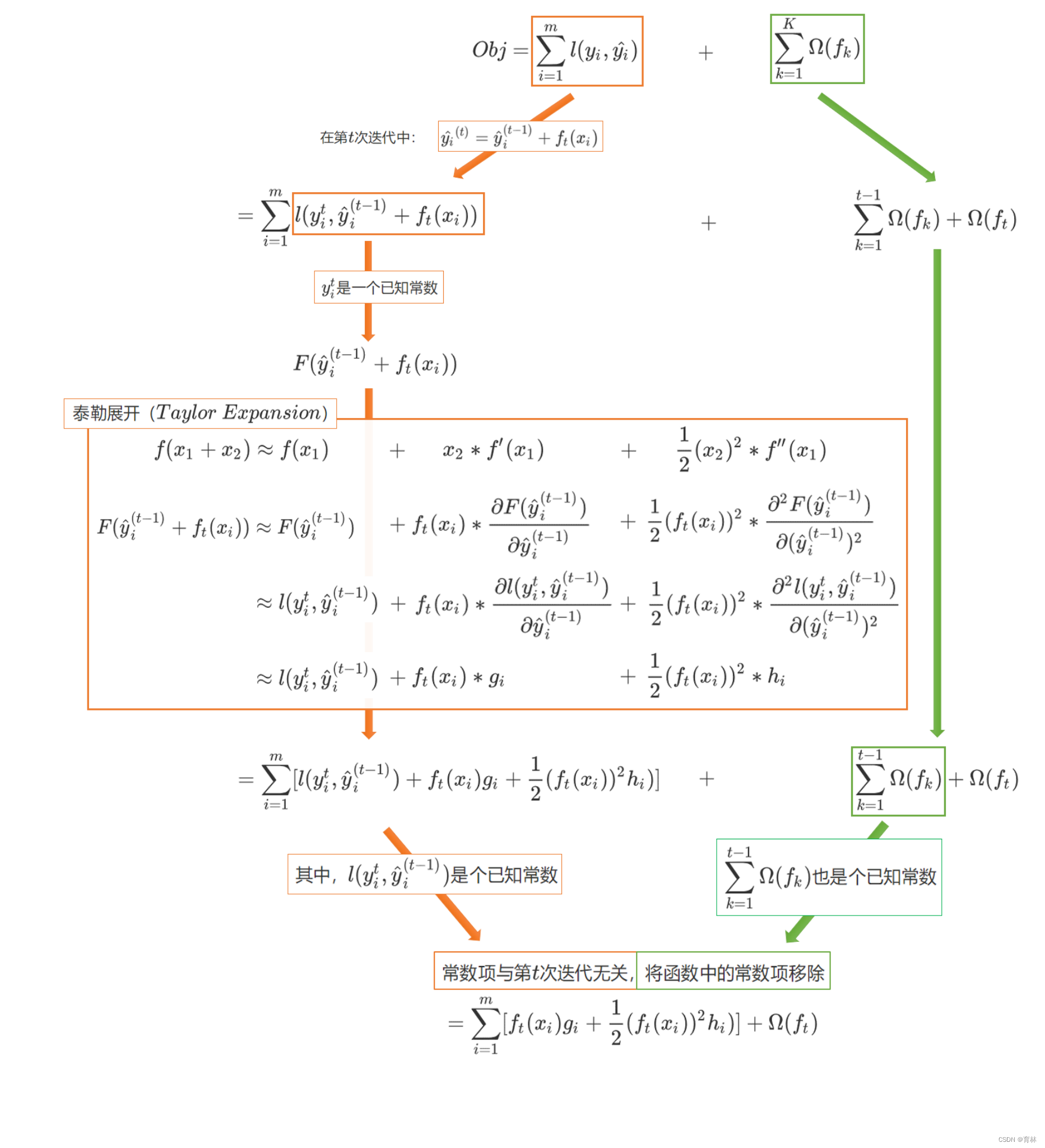
三、求解XGB的目标函数

在求解XGB的目标函数的过程中，我们考虑的是如何能够将目标函数转化成更简单的，与树的结构直接相关的写法，
以此来建立树的结构与模型的效果（包括泛化能力与运行速度）之间的直接联系。也因为这种联系的存在，XGB的目
标函数又被称为“结构分数”。

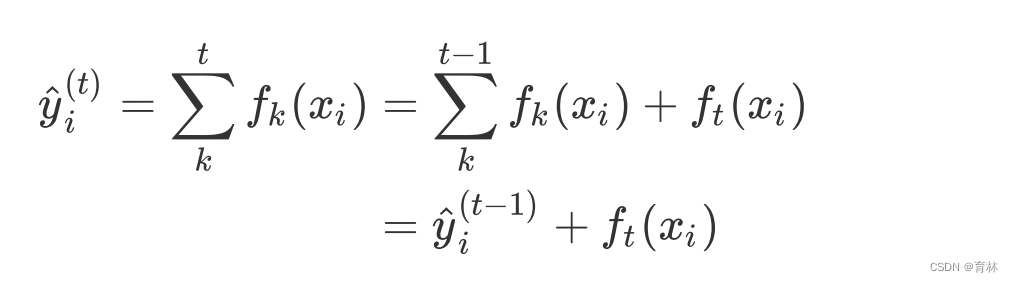
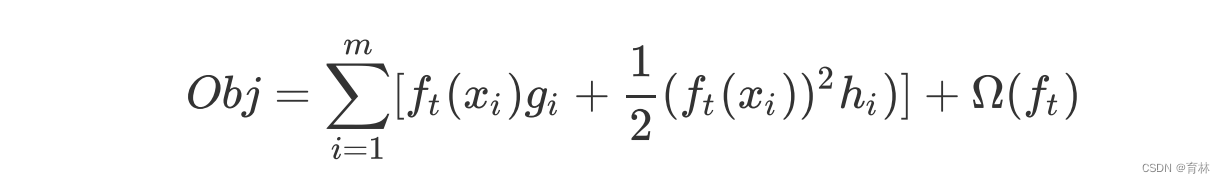
四、参数化决策树 alpha，lambda

当有多棵树的时候，集成模型的回归结果就是所有树的预测分数之和，假设这个集成模型中总共有K棵决策树，则整个模型在这个样本i上给出的预测结果为:


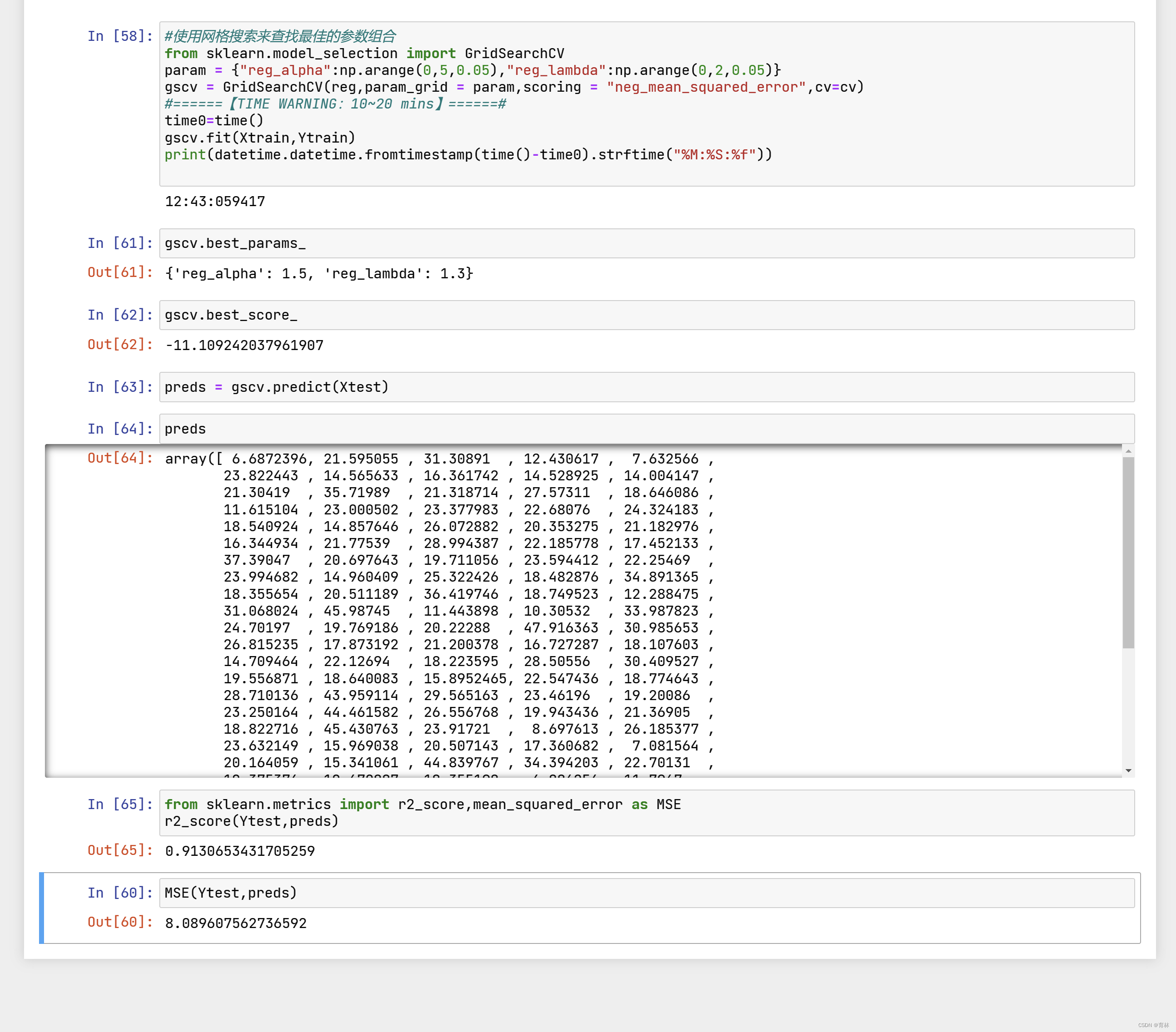
根据我们以往的经验，我们往往认为两种正则化达到的效果是相似的，只不过细节不同。比如在逻辑回归当中，两种
正则化都会压缩θ 参数的大小，只不过L1正则化会让 θ 为0，而L2正则化不会。在XGB中也是如此。当 λ和 α越大，惩罚
越重，正则项所占的比例就越大，在尽全力最小化目标函数的最优化方向下，叶子节点数量就会被压制，模型的复杂
度就越来越低，所以对于天生过拟合的XGB来说，正则化可以一定程度上提升模型效果。
对于两种正则化如何选择的问题，从XGB的默认参数来看，我们优先选择的是L2正则化。当然，如果想尝试L1也不是
不可。两种正则项还可以交互，因此这两个参数的使用其实比较复杂。在实际应用中，正则化参数往往不是我们调参
的最优选择，如果真的希望控制模型复杂度，我们会调整γ 而不是调整这两个正则化参数，因此大家不必过于在意这
两个参数最终如何影响了我们的模型效果。对于树模型来说，还是剪枝参数地位更高更优先。大家只需要理解这两个
参数从数学层面上如何影响我们的模型就足够了。如果我们希望调整 λ和α ，我们往往会使用网格搜索来帮助我们。
在这里，为大家贴出网格搜索的代码和结果供大家分析和学习。

五、寻找最佳树结构：求解 ω与T

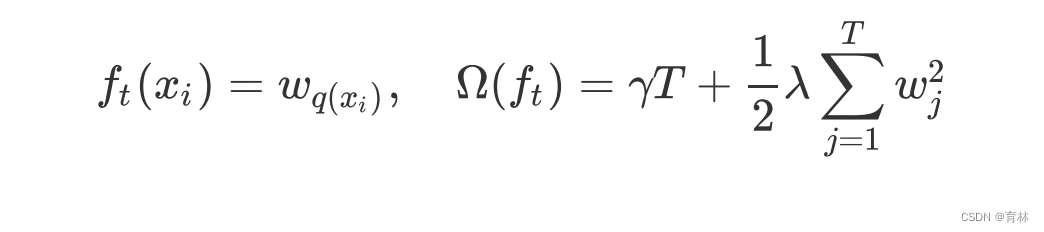
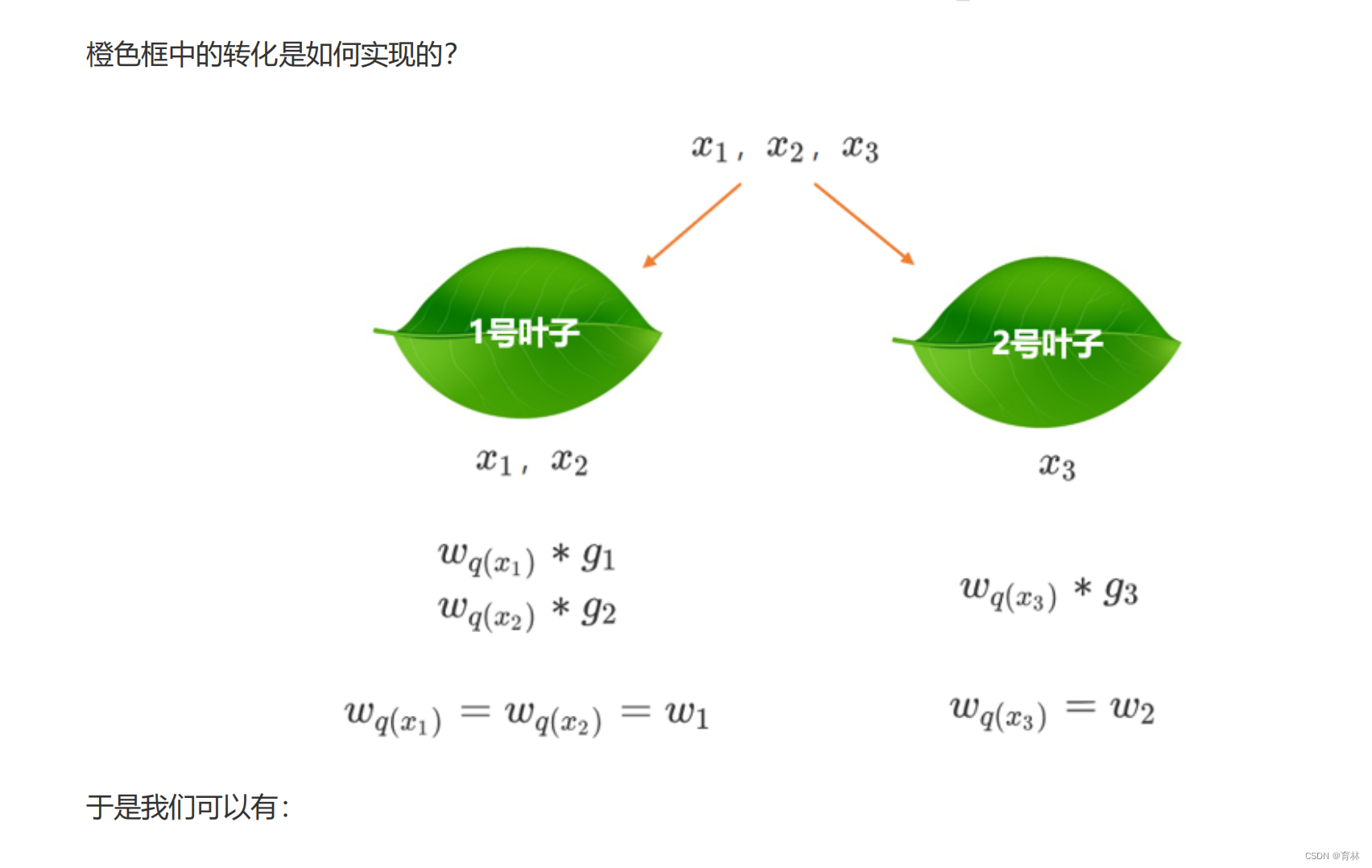
六、寻找最佳分枝：结构分数之差

贪婪算法指的是控制局部最优来达到全局最优的算法，决策树算法本身就是一种使用贪婪算法的方法。XGB作为树的
集成模型，自然也想到采用这样的方法来进行计算，所以我们认为，如果每片叶子都是最优，则整体生成的树结构就
是最优，如此就可以避免去枚举所有可能的树结构。

回忆一下决策树中我们是如何进行计算：我们使用基尼系数或信息熵来衡量分枝之后叶子节点的不纯度，分枝前的信
息熵与分治后的信息熵之差叫做信息增益，信息增益最大的特征上的分枝就被我们选中，当信息增益低于某个阈值
时，就让树停止生长。在XGB中，我们使用的方式是类似的：我们首先使用目标函数来衡量树的结构的优劣，然后让
树从深度0开始生长，每进行一次分枝，我们就计算目标函数减少了多少，当目标函数的降低低于我们设定的某个阈
值时，就让树停止生长。
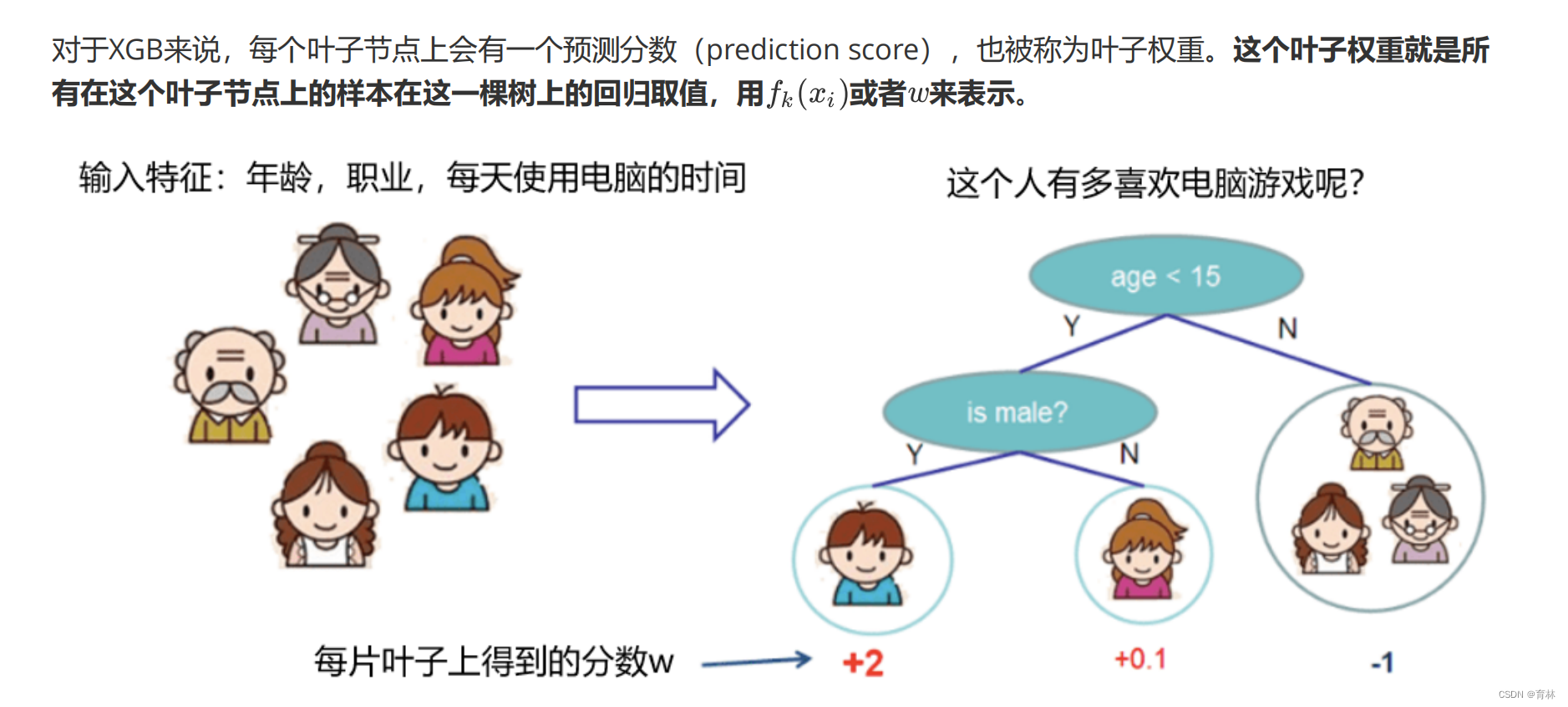
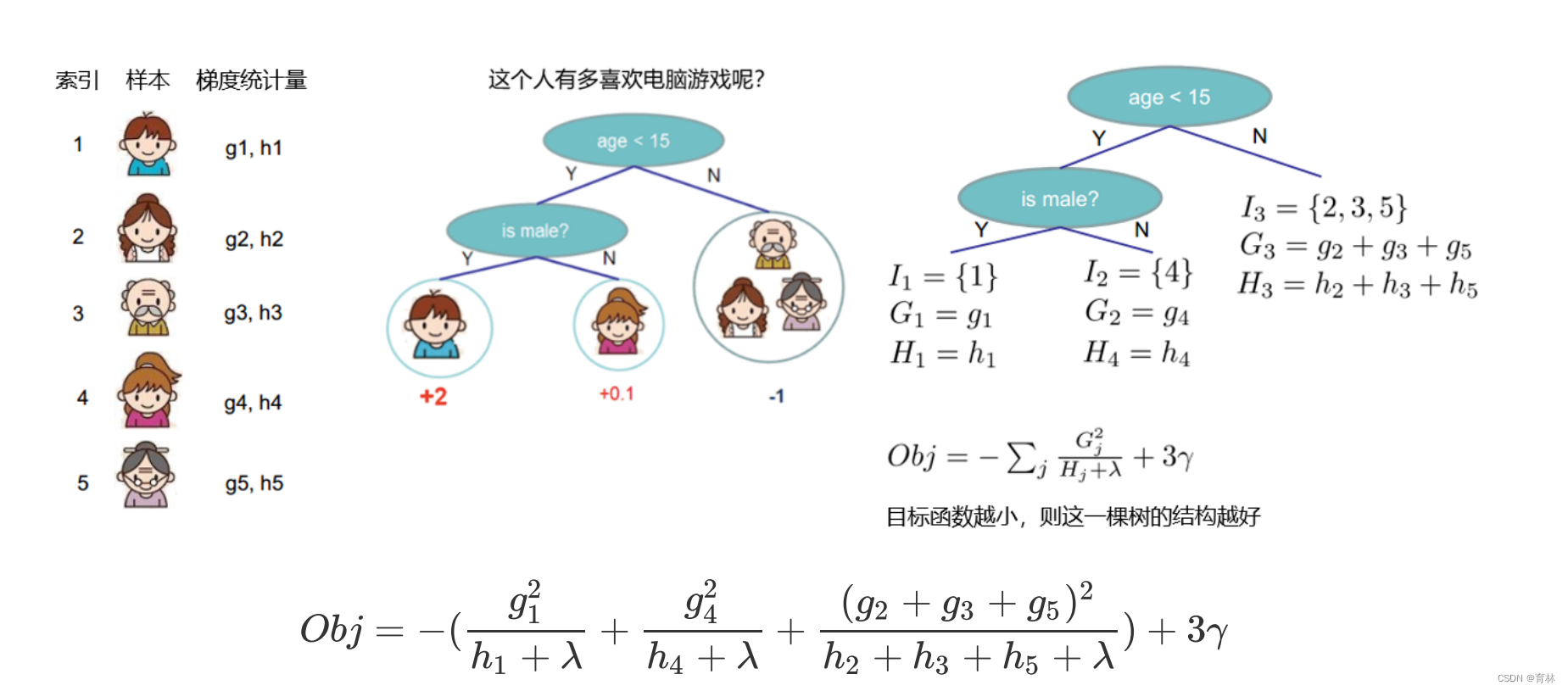
来个具体的例子，在这张图中，我们有中间节点“是否是男性”，这个中间节点下面有两个叶子节点，分别是样本弟弟
和妹妹。我们来看看这个分枝点上，树的结构分数之差如何表示。

七、让树停止生长：重要参数gamma

在逻辑回归中，我们使用参数 tol来设定阈值，并规定如果梯度下降时损失函数减小量小于tol 下降就会停止。在XGB
中，我们规定，只要结构分数之差 Gain是大于0的，即只要目标函数还能够继续减小，我们就允许树继续进行分枝。
也就是说，我们对于目标函数减小量的要求是：

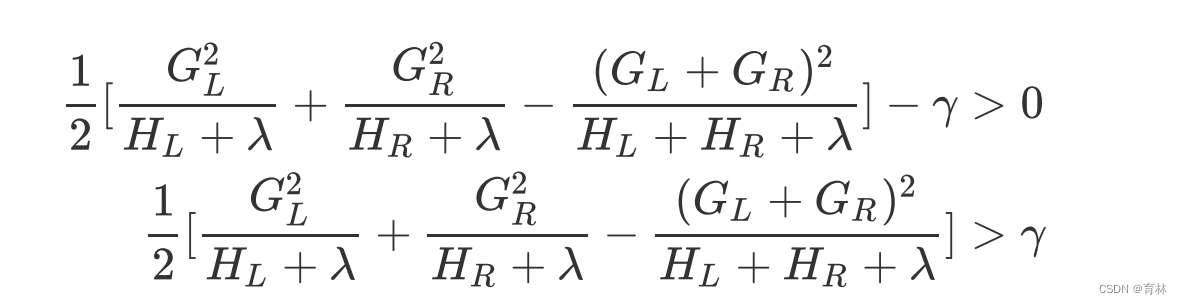
如此，我们可以直接通过设定γ 的大小来让XGB中的树停止生长。γ 因此被定义为，在树的叶节点上进行进一步分枝所
需的最小目标函数减少量，在决策树和随机森林中也有类似的参数（min_split_loss，min_samples_split）。 设定
越大，算法就越保守，树的叶子数量就越少，模型的复杂度就越低。

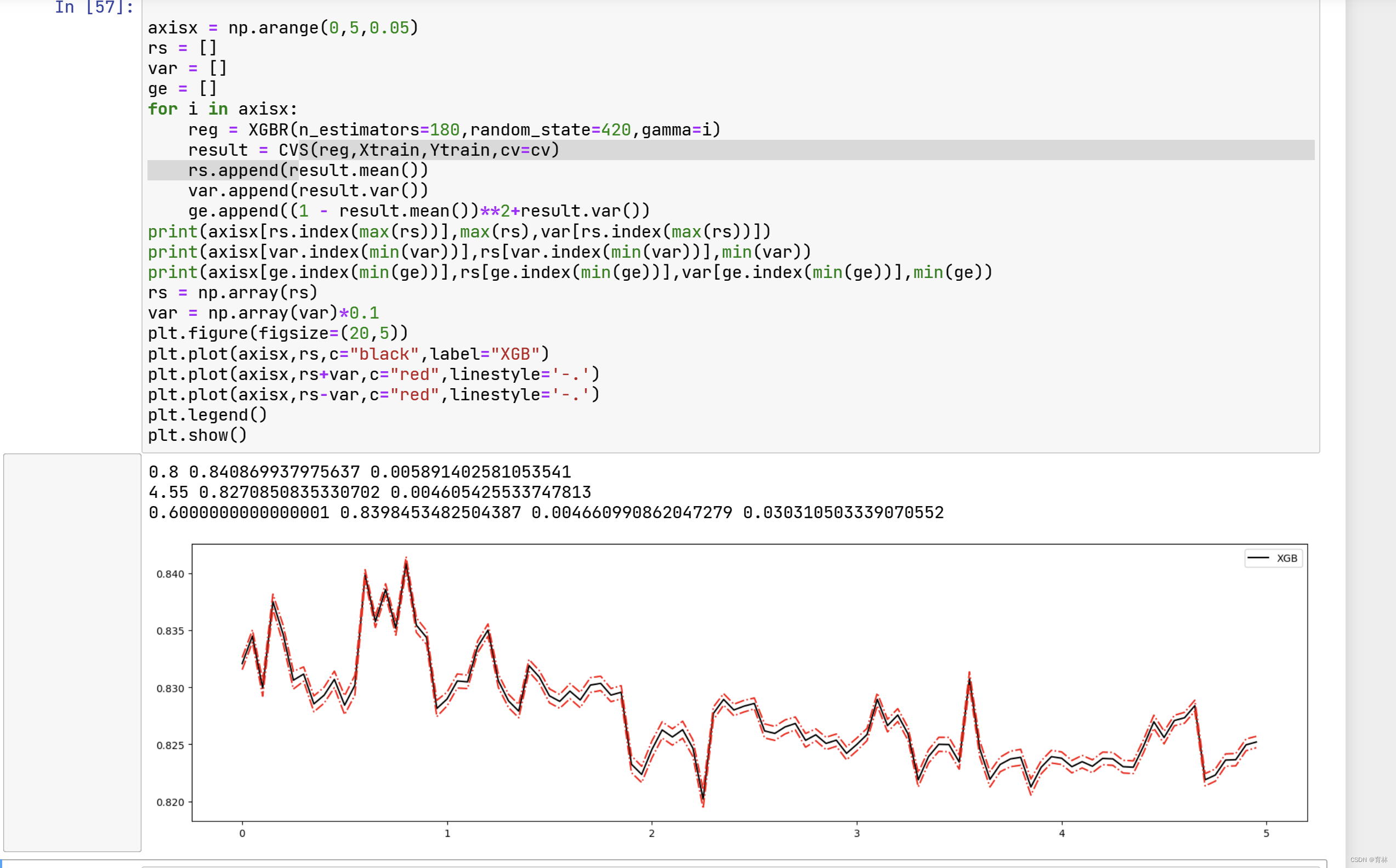
没有规律。

xgboost.cv类

xgboost.cv (params, dtrain, num_boost_round=10, nfold=3, stratified=False, folds=None, metrics=(), obj=None,
feval=None, maximize=False, early_stopping_rounds=None, fpreproc=None, as_pandas=True, verbose_eval=None,
show_stdv=True, seed=0, callbacks=None, shuffle=True)

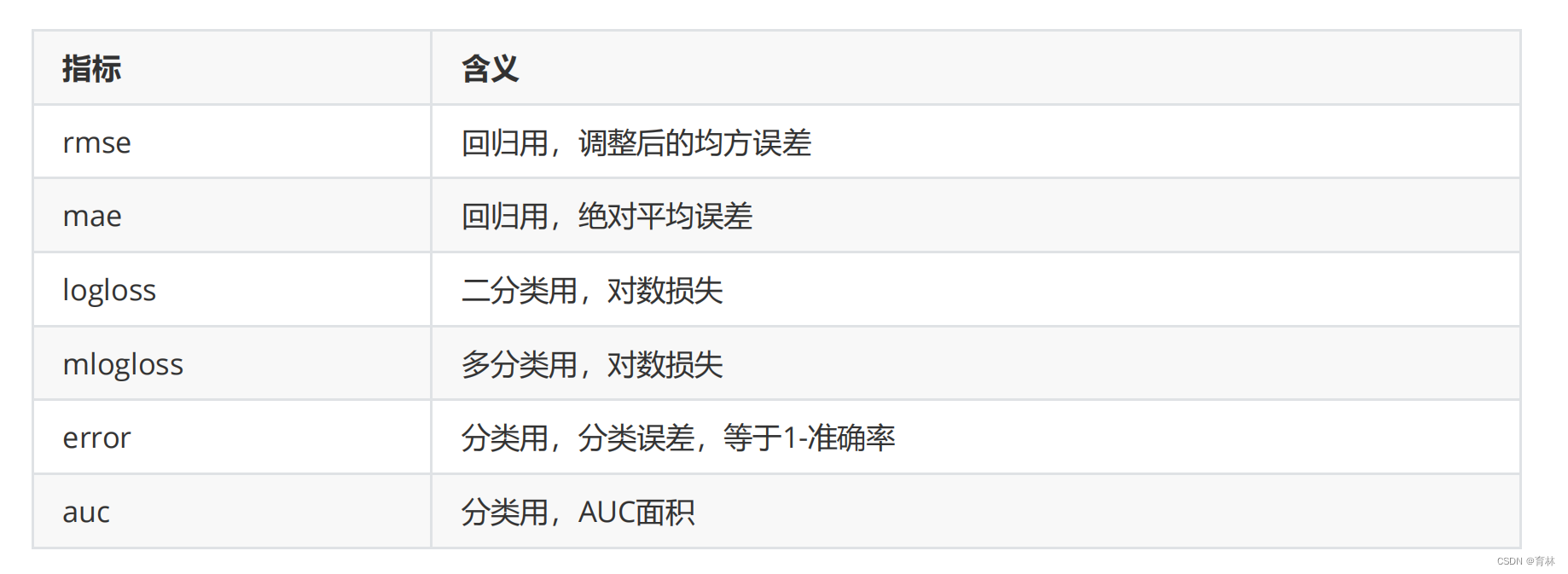
为了使用xgboost.cv，我们必须要熟悉xgboost自带的模型评估指标。xgboost在建库的时候本着大而全的目标，和
sklearn类似，包括了大约20个模型评估指标，然而用于回归和分类的其实只有几个，大部分是用于一些更加高级的
功能比如ranking。来看用于回归和分类的评估指标都有哪些：

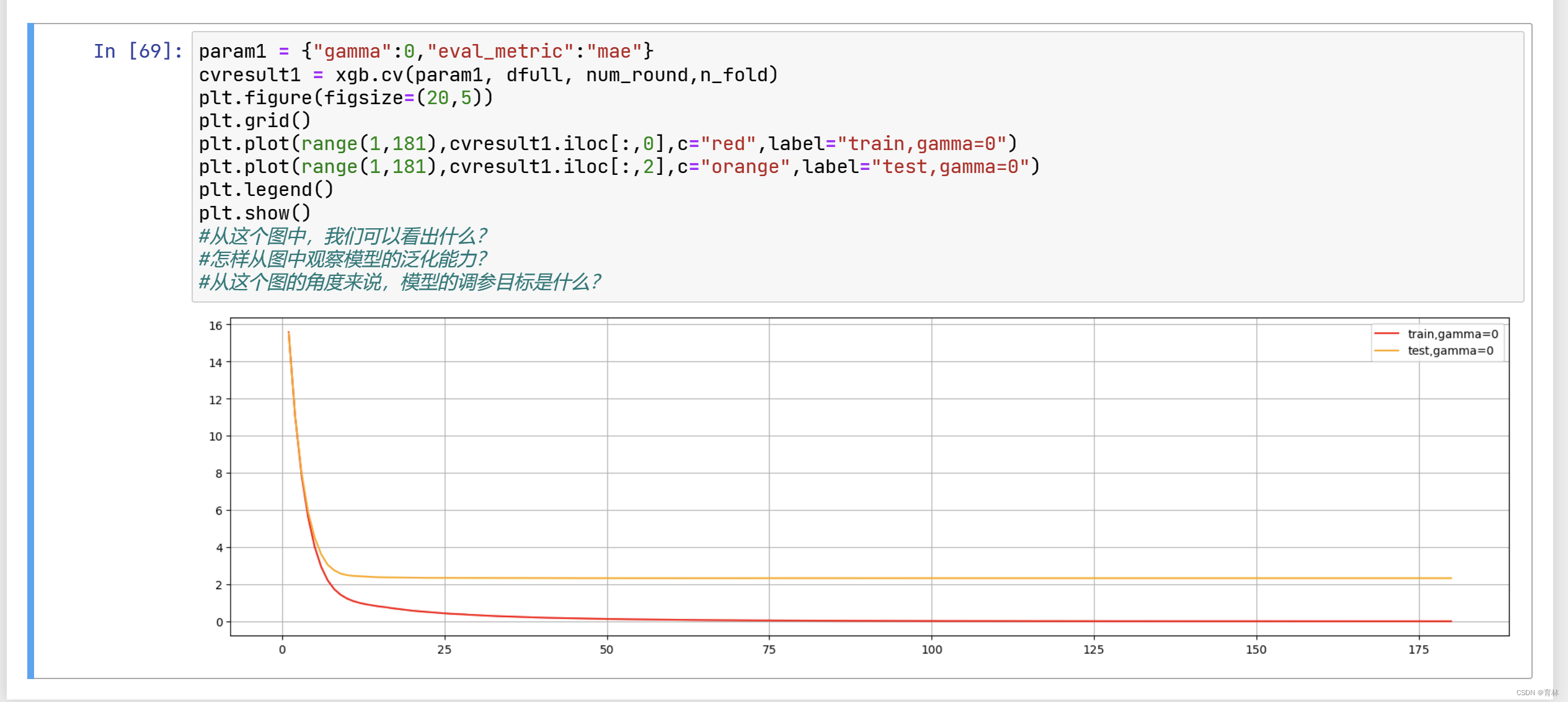
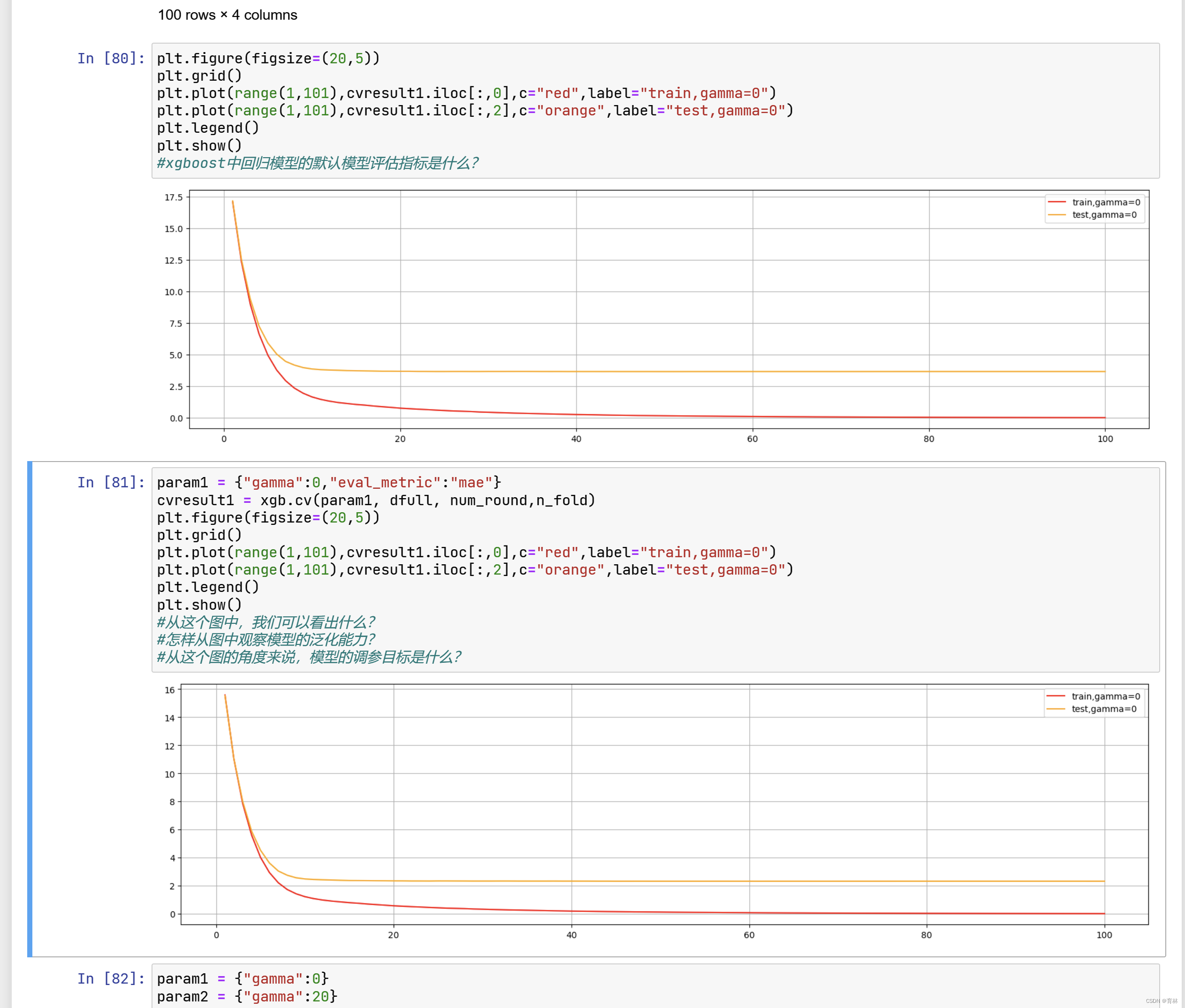
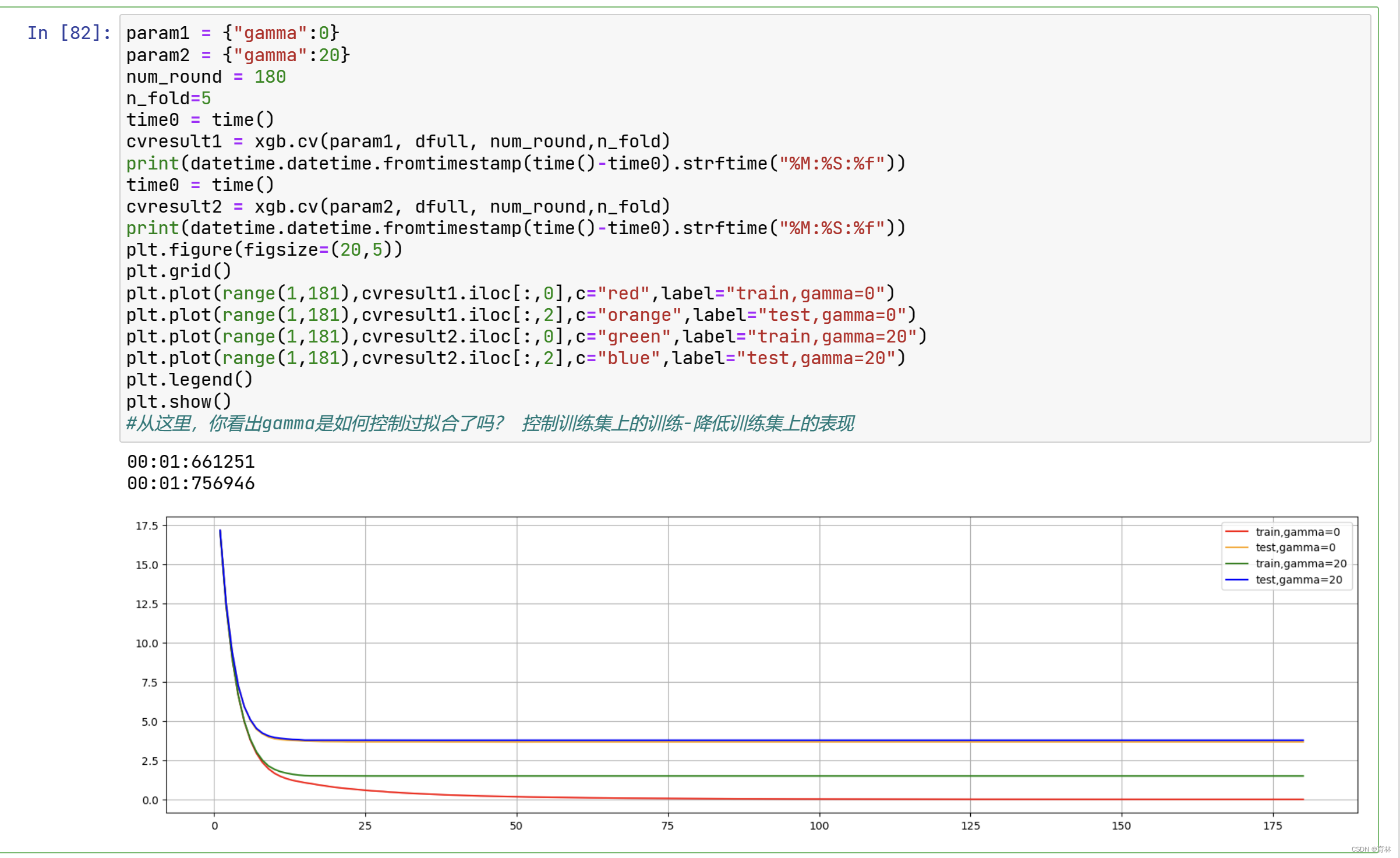
来看看如果我们调整 ，会发生怎样的变化：

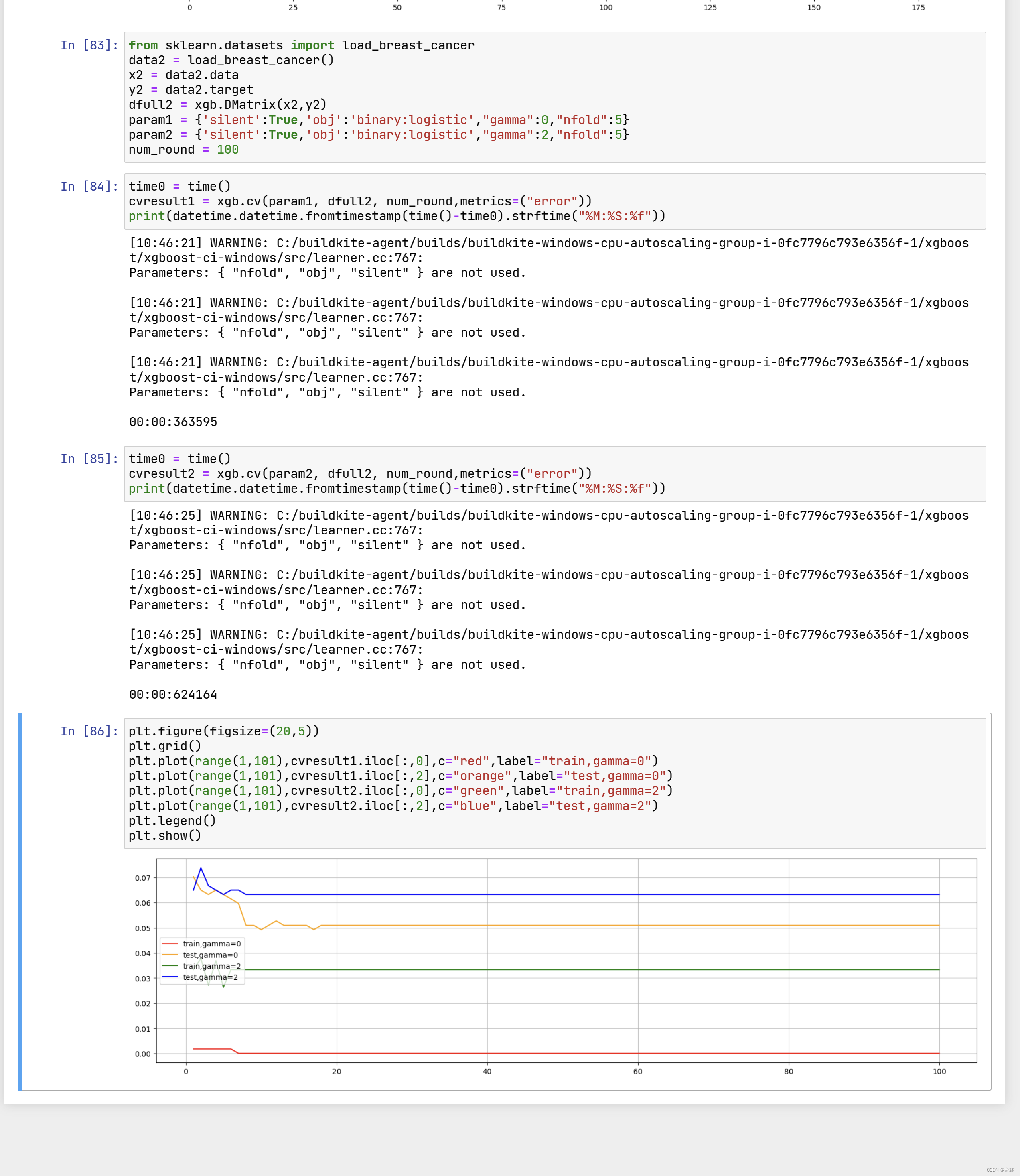
试一个分类的例子：

总结

有了xgboost.cv这个工具，我们的参数调整就容易多了。这个工具可以让我们直接看到参数如何影响了模型的泛化能
力。接下来，我们将重点讲解如何使用xgboost.cv这个类进行参数调整。到这里，所有关于XGBoost目标函数的原理
就讲解完毕了，这个目标函数及这个目标函数所衍生出来的各种数学过程是XGB原理的重中之重，大部分XGB中基于
原理的参数都集中在这个模块之中，到这里大家应该已经基本掌握。