C++数据结构 —— AVL树

news2024/11/24 12:38:40

目录

1.AVL树介绍

2.AVL树如何进行平衡调整

2.1平衡因子

2.2AVL树的插入

2.3左单旋

2.4右单旋

2.5左右双旋

2.6右左双旋

2.8完整代码

3.测试用例

4.验证是否为AVL树

1.AVL树介绍

AVL树是map/set/multimap/multi/set等容器的一种底层结构，其本质就是一颗二叉搜索树。但因为二叉搜索树很容易退化成单支树，所以AVL树便是对二叉搜索树进行升级改造，使其平衡。

AVL进行平衡的方法为：向二叉搜索树插入节点，保证每个节点的左右子树高度差不超过1(可以包括1)，如果确实达不到这种要求，就需要通过特定的算法来达到这样的要求。一颗AVL树可以是空树，也可以是具有以下性质的二叉搜索树：

        1.每个节点的左右子树都是AVL树

        2.每个节点的左右子树的高度差不超过1(可以包括1)

AVL树的搜索时间复杂度可以一直维持在O(log_2N)。

2.AVL树如何进行平衡调整

2.1平衡因子

平衡因子记录当前节点的左右子树的高度差。通过维护平衡因子，在设计AVL树时，可以很方便的判断出，什么情况下该使用什么样的调整算法。我们默认认为，左右子树高度差的计算公式为：右子树高度 - 左子树高度。

那么AVL树的节点可以这样定义：

template <class K>
struct AVLTreeNode
{
	AVLTreeNode<K>* _left;
	AVLTreeNode<K>* _right;
	AVLTreeNode<K>* _parent;	//指向父节点

	K _key;

	int _bf;	//平衡因子

	AVLTreeNode(const K& key)
		:_left(nullptr), _right(nullptr), _parent(nullptr),_key(key), _bf(0)
	{}
};

2.2AVL树的插入

节点进行插入的时候，我们需要维护平衡因子，还有维护指向父节点的指针。所以，我们的插入思路，可以这样写：

template<class K>
class AVLTree
{
	typedef AVLTreeNode<K> Node;
public:
	bool insert(const K& key)
	{
		if (_root == nullptr)
		{
			_root = new Node(key);
			return true;
		}

		Node* parent = nullptr;	//记录cur节点的上一个节点
		Node* cur = _root;
		while (cur)
		{
			if (key < cur->_key)
			{
				parent = cur;
				cur = cur->_left;
			}
			else if (key > cur->_key)
			{
				parent = cur;
				cur = cur->_right;
			}
			else
			{
				// key和树中的某一键值相等，退出
				return false;
			}
		}

		// 找到了新节点的插入位置
		cur = new Node(key);
		
		if (key < parent->_key)
		{
			parent->_left = cur;
			cur->_parent = parent;	//注意维护指向父节点的指针
		}
		else if (key > parent->_key)
		{
			parent->_right = cur;
			cur->_parent = parent;
		}

		// 现在需要维护平衡因子:右子树高度 - 左子树高度

		while (parent)	//parent节点不为空时，就需要对平衡因子维护
		{
			if (parent->_left == cur)	//当新增节点在parent的左边时
			{
				parent->_bf--;
			}
			else if (parent->_right == cur)	//新增节点在parent的右边时
			{
				parent->_bf++;
			}

			if (parent->_bf == 0)	//更新平衡因子后，parent的平衡因子为0，就说明左右子树高度相等
									//不需要进行处理
			{
				break;
			}
			else if (parent->_bf == 1 || parent->_bf == -1)	//parent的左子树或右子树的高度增加了
															//就需要往上更新平衡因子
			{
				cur = parent;
				parent = parent->_parent;
			}
			else if (parent->_bf == 2 || parent->_bf == -2)	//parent的左右子树高度差不符合要求了
															//需要根据平衡因子的关系来选用特定的算法调整
			{
				// ...调整算法
			}
			else
			{
				assert(false);	//如果发生断言错误，则说明代码设计的有问题
			}
		}

		return true;
	}
private:
	Node* _root = nullptr;
};

现在来详细解释一下更新平衡因子的算法：

 同样的如上图所示，如果键值为9的节点作为根节点，那它势必是最后更新到的节点。所以在上面的代码中使用了while(parent)语句，当parent为空时就不进入更新平衡因子。

2.3左单旋

如果在较高右子树的右侧插入一个新节点，就需要使用左单旋算法：

void RotateL(Node* parent)
	{
		Node* cur = parent->_right;
		Node* curL = cur->_left;	//cur的左树

		parent->_right = curL;	//cur的左树变成parent的右树
		if (curL)
		{
			curL->_parent = parent;
		}

		Node* oldParent = parent->_parent;	//记录parent的父节点
		parent->_parent = cur;	//cur作为parent的父节点
		cur->_left = parent;	//parent作为cur的左树

		if (oldParent == nullptr)	
		{
			_root = cur;	//直接让cur作为根节点(因为parent的旧父节点为空)
			cur->_parent = nullptr;
		}
		else
		{
			if (oldParent->_left == parent)
			{
				oldParent->_left = cur;
				cur->_parent = oldParent;
			}
			else if (oldParent->_right == parent)
			{
				oldParent->_right = cur;
				cur->_parent = oldParent;
			}
		}
		
		parent->_bf = cur->_bf = 0;	//平衡因子都置为0(推理得出结论)
	}

2.4右单旋

如果在较高左子树的左侧插入一个新节点，就需要使用右单旋算法：

void RotateR(Node* parent)
{
	Node* cur = parent->_left;
	Node* curR = cur->_right;

	parent->_left = curR;	//cur的右树作为parent的左树
	if (curR)
	{
		curR->_parent = parent;
	}

	Node* oldParent = parent->_parent;
	parent->_parent = cur;	
	cur->_right = parent;	//parent作为cur的右树

	if (oldParent == nullptr)
	{
		_root = cur;
		cur->_parent = nullptr;
	}
	else
	{
		if (oldParent->_left == parent)
		{
			oldParent->_left = cur;
			cur->_parent = oldParent;
		}
		else if (oldParent->_right == parent)
		{
			oldParent->_right = cur;
			cur->_parent = oldParent;
		}
	}

	parent->_bf = cur->_bf = 0;
}

2.5左右双旋

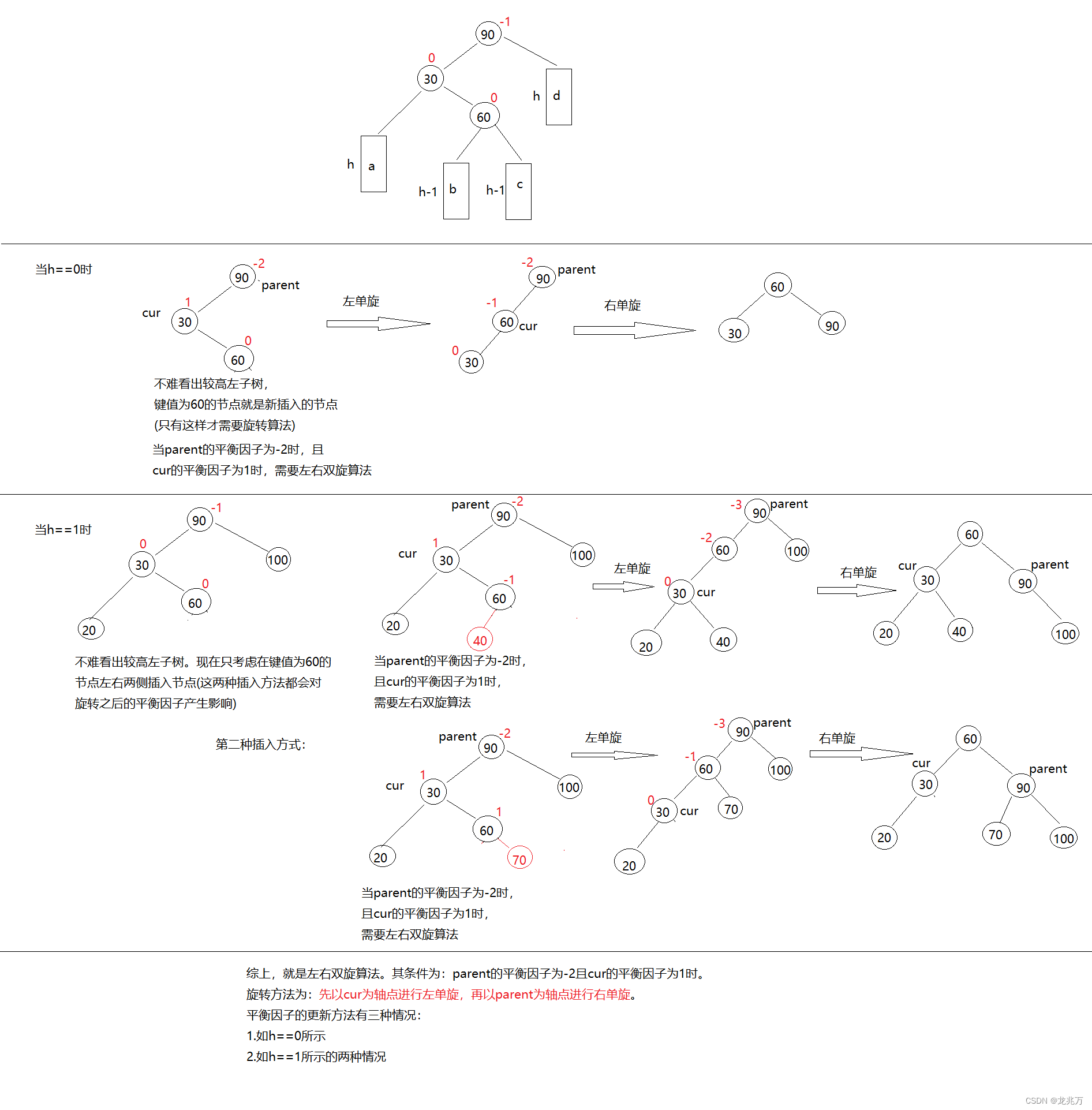
如果在较高左子树的右侧插入一个新节点，就需要使用左右双旋算法：

void RotateLR(Node* parent)
{
	Node* cur = parent->_left;
	Node* curR = cur->_right;

	int bf = curR->_bf;	//旋转之前记录一下cur的孩子节点的平衡因子

	RotateL(cur);
	RotateR(parent);

	if (bf == 0)	//如图所示h==0时
	{
		parent->_bf = cur->_bf = curR->_bf = 0;
	}
	else if (bf == -1)	//如图所示h==1时第一种插入方式
	{
		parent->_bf = 1;
		cur->_bf = 0;
		curR->_bf = 0;
	}
	else if (bf == 1)	//如图所示h==1时第二种插入方式
	{
		parent->_bf = 0;
		cur->_bf = -1;
		curR->_bf = 0;
	}
}

2.6右左双旋

如果在较高右子树的左侧插入一个新节点，就需要使用右左双旋算法：

void RotateRL(Node* parent)
{
	Node* cur = parent->_right;
	Node* curL = cur->_left;

	int bf = curL->_bf;

	RotateR(cur);
	RotateL(parent);

	if (bf == 0)	//h==0时
	{
		parent->_bf = cur->_bf = curL->_bf = 0;
	}
	else if (bf == -1)
	{
		parent->_bf = 0;
		cur->_bf = 1;
		curL->_bf = 0;
	}
	else if (bf == 1)
	{
		parent->_bf = -1;
		cur->_bf = 0;
		curL->_bf = 0;
	}
}

2.8完整代码

template <class K>
struct AVLTreeNode
{
	AVLTreeNode<K>* _left;
	AVLTreeNode<K>* _right;
	AVLTreeNode<K>* _parent;	//指向父节点

	K _key;

	int _bf;	//平衡因子

	AVLTreeNode(const K& key)
		:_left(nullptr), _right(nullptr), _parent(nullptr),_key(key), _bf(0)
	{}
};

template<class K>
class AVLTree
{
	typedef AVLTreeNode<K> Node;
public:
	bool insert(const K& key)
	{  
		if (_root == nullptr)
		{
			_root = new Node(key);
			return true;
		}

		Node* parent = nullptr;	//记录cur节点的上一个节点
		Node* cur = _root;
		while (cur)
		{
			if (key < cur->_key)
			{
				parent = cur;
				cur = cur->_left;
			}
			else if (key > cur->_key)
			{
				parent = cur;
				cur = cur->_right;
			}
			else
			{
				// key和树中的某一键值相等，退出
				return false;
			}
		}

		// 找到了新节点的插入位置
		cur = new Node(key);

		if (key < parent->_key)
		{
			parent->_left = cur;
			cur->_parent = parent;	//注意维护指向父节点的指针
		}
		else if (key > parent->_key)
		{
			parent->_right = cur;
			cur->_parent = parent;
		}

		// 现在需要维护平衡因子:右子树高度 - 左子树高度

	while (parent)	//parent节点不为空时，就需要对平衡因子维护
	{
		if (parent->_left == cur)	//当新增节点在parent的左边时
		{
			parent->_bf--;
		}
		else if (parent->_right == cur)	//新增节点在parent的右边时
		{
			parent->_bf++;
		}

		if (parent->_bf == 0)	//更新平衡因子后，parent的平衡因子为0，就说明左右子树高度相等
								//不需要进行处理
		{
			break;
		}
		else if (parent->_bf == 1 || parent->_bf == -1)	//parent的左子树或右子树的高度增加了
														//就需要往上更新平衡因子
		{
			cur = parent;
			parent = parent->_parent;
		}
		else if (parent->_bf == 2 || parent->_bf == -2)	//parent的左右子树高度差不符合要求了
														//需要根据平衡因子的关系来选用特定的算法调整
		{
			// ...调整算法
			if (parent->_bf == 2 && cur->_bf == 1)
			{
				RotateL(parent);
			}
			else if (parent->_bf == -2 && cur->_bf == -1)
			{
				RotateR(parent);
			}
			else if (parent->_bf == -2 && cur->_bf == 1)
			{
				RotateLR(parent);
			}
			else if (parent->_bf = 2 && cur->_bf == -1)
			{
				RotateRL(parent);
			}
			else
			{
				assert(false);
			}

			break;		//调整完即可视为插入完毕
		}
		else
		{
			assert(false);	//如果发生断言错误，则说明代码设计的有问题
		}
	}

		return true;
	}

	void RotateL(Node* parent)
	{
		Node* cur = parent->_right;
		Node* curL = cur->_left;	//cur的左树

		parent->_right = curL;	//cur的左树变成parent的右树
		if (curL)
		{
			curL->_parent = parent;
		}

		Node* oldParent = parent->_parent;	//记录parent的父节点
		parent->_parent = cur;	//cur作为parent的父节点
		cur->_left = parent;	//parent作为cur的左树

		if (oldParent == nullptr)	
		{
			_root = cur;	//直接让cur作为根节点(因为parent的旧父节点为空)
			cur->_parent = nullptr;
		}
		else
		{
			if (oldParent->_left == parent)
			{
				oldParent->_left = cur;
				cur->_parent = oldParent;
			}
			else if (oldParent->_right == parent)
			{
				oldParent->_right = cur;
				cur->_parent = oldParent;
			}
		}
		
		parent->_bf = cur->_bf = 0;	//平衡因子都置为0(推理得出结论)
	}

	void RotateR(Node* parent)
	{
		Node* cur = parent->_left;
		Node* curR = cur->_right;


		parent->_left = curR;	//cur的右树作为parent的左树
		if (curR)
		{
			curR->_parent = parent;
		}

		Node* oldParent = parent->_parent;
		parent->_parent = cur;	
		cur->_right = parent;	//parent作为cur的右树

		if (oldParent == nullptr)
		{
			_root = cur;
			cur->_parent = nullptr;
		}
		else
		{
			if (oldParent->_left == parent)
			{
				oldParent->_left = cur;
				cur->_parent = oldParent;
			}
			else if (oldParent->_right == parent)
			{
				oldParent->_right = cur;
				cur->_parent = oldParent;
			}
		}

		parent->_bf = cur->_bf = 0;
	}


	void RotateLR(Node* parent)
	{
		Node* cur = parent->_left;
		Node* curR = cur->_right;

		int bf = curR->_bf;	//旋转之前记录一下cur的孩子节点的平衡因子

		RotateL(cur);
		RotateR(parent);

		if (bf == 0)	//如图所示h==0时
		{
			parent->_bf = cur->_bf = curR->_bf = 0;
		}
		else if (bf == -1)	//如图所示h==1时第一种插入方式
		{
			parent->_bf = 1;
			cur->_bf = 0;
			curR->_bf = 0;
		}
		else if (bf == 1)	//如图所示h==1时第二种插入方式
		{
			parent->_bf = 0;
			cur->_bf = -1;
			curR->_bf = 0;
		}
	}


	void RotateRL(Node* parent)
	{
		Node* cur = parent->_right;
		Node* curL = cur->_left;

		int bf = curL->_bf;

		RotateR(cur);
		RotateL(parent);

		if (bf == 0)	//h==0时
		{
			parent->_bf = cur->_bf = curL->_bf = 0;
		}
		else if (bf == -1)
		{
			parent->_bf = 0;
			cur->_bf = 1;
			curL->_bf = 0;
		}
		else if (bf == 1)
		{
			parent->_bf = -1;
			cur->_bf = 0;
			curL->_bf = 0;
		}
	}


	void level()
	{
		vector<vector<string>> vec;
		if (_root == nullptr)
		{
			return;
		}

		queue<Node*> q;
		q.push(_root);

		while (!q.empty())
		{
			int size = q.size();
			vector<string> tmp;
			while (size--)
			{
				Node* front = q.front();
				q.pop();

				if (front)
				{
					tmp.push_back(to_string(front->_key));
				}
				else
				{
					tmp.push_back("nullptr");
				}

				if (front)
				{
					if (front->_left)
					{
						q.push(front->_left);
					}
					else
					{
						q.push(nullptr);
					}

					if (front->_right)
					{
						q.push(front->_right);
					}
					else
					{
						q.push(nullptr);
					}
				}

			}
			vec.push_back(tmp);


		}

		for (int i = 0; i < vec.size(); i++)
		{
			for (int j = 0; j < vec[i].size(); j++)
			{
				cout << vec[i][j] << " ";
			}
			cout << endl;
		}
	}


	bool isAVLTree()
	{
		return isAVLTree(_root);
	}

	bool isAVLTree(Node* root)
	{
		if (root == nullptr)
		{
			return true;
		}

		int leftHeight = height(root->_left);
		int rightHeight = height(root->_right);

		if (root->_bf != (rightHeight - leftHeight))
		{
			cout << root->_key << "平衡因子出错:" << root->_bf << endl;
			return false;
		}

		return abs(rightHeight - leftHeight) < 2
			&& isAVLTree(root->_left)
			&& isAVLTree(root->_right);
	}


	int height(Node* root)
	{
		if (root == nullptr)
		{
			return 0;
		}

		int lh = height(root->_left);
		int rh = height(root->_right);

		return lh > rh ? lh + 1 : rh + 1;
	}
private:
	Node* _root = nullptr;
};

3.测试用例

二叉树非线性表，所以如果代码出现问题是很难看出问题的。所以这里给出两组测试用例，以便更早的发现问题。

常规场景：

        {16,3,7,11,9,26,18,14,15}

特殊场景：

        {4,2,6,1,3,5,15,7,16,14}

可以使用中序遍历或层序遍历来观察输出结果是否符合自己的预期。

4.验证是否为AVL树

前面一直强调，AVL树的每个节点左右子树的高度差不超过1。现在只需要写一个程序判断是否符合这个条件即可。

bool isAVLTree()
{
	return isAVLTree(_root);
}

bool isAVLTree(Node* root)
{
	if (root == nullptr)
	{
		return true;
	}

	int leftHeight = height(root->_left);
	int rightHeight = height(root->_right);

	if (root->_bf != (rightHeight - leftHeight))
	{
		cout << root->_key << "平衡因子出错:" << root->_bf << endl;
		return false;
	}

	return abs(rightHeight - leftHeight) < 2
		&& isAVLTree(root->_left)
		&& isAVLTree(root->_right);
}


int height(Node* root)
{
	if (root == nullptr)
	{
		return 0;
	}

	int lh = height(root->_left);
	int rh = height(root->_right);

	return lh > rh ? lh + 1 : rh + 1;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/373950.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

推荐系统算法总览【持续学习ing】

推荐系统算法总览【持续学习ing】

推荐系统整体知识架构 推荐模型发展 工业 CTR模型的三个改进大点&#xff1a;显性特征交叉&#xff0c; 特征重要度&#xff0c; user历史信息的挖掘 显性特征交叉&#xff1a; 针对的是隐性无脑交叉的DNN的不足&#xff0c; 针对一些重要的关键特征进行显性特征交叉&#xf…
阅读更多...
Java中BIO、NIO和AIO的区别和应用场景

Java中BIO、NIO和AIO的区别和应用场景

IO的方式通常分为几种&#xff0c;同步阻塞的BIO、同步非阻塞的NIO、异步非阻塞的AIO。 一、BIO 在JDK1.4出来之前&#xff0c;我们建立网络连接的时候采用BIO模式&#xff0c;需要先在服务端启动一个ServerSocket&#xff0c;然后在客户端启动Socket来对服务端进行通信&#…
阅读更多...
学习网安需要了解的一些基础知识

学习网安需要了解的一些基础知识

P1.基本概念 1.POC/EXP POC(proof of concept)常指一段漏洞验证代码&#xff1b;EXP(exploit)指利用系统漏洞进行攻击的动作 PoC是证明漏洞存在的,而 Exp 是利用这个漏洞进一步进行攻击&#xff0c;先有POC&#xff0c;才有EXP 2.Payload/shellcode payload&#xff0…
阅读更多...
【奶奶看了也不会】AI绘画 Mac安装stable-diffusion-webui绘制AI妹子保姆级教程

【奶奶看了也不会】AI绘画 Mac安装stable-diffusion-webui绘制AI妹子保姆级教程

1.作品图 2.准备工作 目前网上能搜到的stable-diffusion-webui的安装教程都是Window和Mac M1芯片的&#xff0c;而对于因特尔芯片的文章少之又少&#xff0c;这就导致我们还在用老Intel 芯片的Mac本&#xff0c;看着别人生成美女图片只能眼馋。所以小卷这周末折腾了一天&#…
阅读更多...
Random（一）高并发问题，ThreadLocalRandom源码解析

Random（一）高并发问题，ThreadLocalRandom源码解析

目录1.什么是伪随机数&#xff1f;2.Random2.1 使用示例2.2 什么种子重复&#xff0c;随机数会重复&#xff1f;2.3 nextInt() 源码分析2.4 线程安全的实现2.5 高并发问题3.ThreadLocalRandom3.1 使用示例3.2 current() 源码解析3.2.1 Thread中保存的变量&#xff1a;3.2.2 Thr…
阅读更多...
2023最新谷粒商城笔记之MQ消息队列篇（全文总共13万字，超详细）

2023最新谷粒商城笔记之MQ消息队列篇（全文总共13万字，超详细）

MQ消息队列 其实队列JDK中本身就有&#xff0c;不过这种队列也只能单体服务可能会使用&#xff0c;一旦项目使用的分布式架构&#xff0c;那么一定还是需要用到一个消息中间件的。我们引入消息队列的原因就是对我们的页面相应速度再优化&#xff0c;让用户的体验更好&#xff…
阅读更多...
Ae：使用占位符

Ae：使用占位符

占位符 Placeholder本质上是一个静止的彩条图像&#xff0c;用来临时代替缺失的素材。自动占位符当 Ae 找不到源素材&#xff0c;比如被移动、删除或重命名&#xff0c;Ae 将自动生成占位符&#xff0c;在项目面板中用斜体显示&#xff0c;使用该素材的任何合成将用一个占位符图…
阅读更多...
【R统计】R语言相关性分析及其可视化

【R统计】R语言相关性分析及其可视化

&#x1f482; 个人信息&#xff1a;酷在前行&#x1f44d; 版权: 博文由【酷在前行】原创、需要转载请联系博主&#x1f440; 如果博文对您有帮助&#xff0c;欢迎点赞、关注、收藏 订阅专栏&#x1f516; 本文收录于【R统计】&#xff0c;该专栏主要介绍R语言实现统计分析的…
阅读更多...
libxlsxwriter簇状柱形图绘制

libxlsxwriter簇状柱形图绘制

libxlsxwriter的功能覆盖面很大&#xff0c;今天一起来看一下如何用这个库来生成带有簇状柱形图的表格。 1 簇形柱状图 首先来看一下Excel的样例表格&#xff0c;簇状柱形图往往是用来对比若干“系列”的数据在某一时间段内&#xff0c;或某一情境下的差异情况。在商务领域还…
阅读更多...
小白量化《穿云箭集群量化》（4）指标公式写策略

小白量化《穿云箭集群量化》（4）指标公式写策略

小白量化《穿云箭集群量化》&#xff08;4&#xff09;指标公式写策略 穿云箭量化平台支持中文Python写量化策略&#xff0c;同时也直接支持股票公式指标写策略。下面我们看看是如何实现的。 股票软件的指标公式语法是一样的&#xff0c;不同仅仅是个别函数或绘图函数或绘图命令…
阅读更多...
java多态理解和底层实现原理剖析

java多态理解和底层实现原理剖析

java多态理解和底层实现原理剖析多态怎么理解java中方法调用指令invokespecial和invokevirtual指令的区别invokeinterface指令方法表接口方法调用为什么不能利用方法表快速定位小结多态怎么理解 抽象事务的多种具体表现&#xff0c;称为事务的多态性。我们在编码过程中通常都是…
阅读更多...
计算机网络 第4章 作业1

计算机网络 第4章 作业1

一、选择题 1. 由网络层负责差错控制与流量控制,使分组按序被递交的传输方式是_________&#xff08;C&#xff09; A&#xff0e;电路交换 B&#xff0e;报文交换 C&#xff0e;基于虚电路的分组交换 D&#xff0e;基于数据报的分组交换 2. TCP/IP 参考…
阅读更多...
Bunifu.UI.WinForms 6.0.2 Crack

Bunifu.UI.WinForms 6.0.2 Crack

Bunifu.UI.WinForms为 WinForms创建令人惊叹的UI Bunifu.UI.WinForms我们为您提供了现代化的快速用户界面控件。用于 WinForms C# 和 VB.NET 应用程序开发的完美 UI 工具 简单 Bunifu.UI.WinForms没有臃肿的特征。正是您构建令人惊叹的 WinForms 应用程序所需要的。只需拖放然…
阅读更多...
计算机网络高频知识点

计算机网络高频知识点

目录 一、http状态码 二、强缓存与协商缓存 三、简单请求与复杂请求 四、PUT 请求类型 五、GET请求类型 六、GET 和 POST 的区别 七、跨域 1、什么时候会跨域 2、解决方式 八、计算机网络的七层协议与五层协议分别指的是什么 1、七层协议 2、五层协议 九、计算机网…
阅读更多...
监控生产环境中的机器学习模型

监控生产环境中的机器学习模型

简介 一旦您将机器学习模型部署到生产环境中&#xff0c;很快就会发现工作还没有结束。 在许多方面&#xff0c;旅程才刚刚开始。你怎么知道你的模型的行为是否符合你的预期&#xff1f;下周/月/年&#xff0c;当客户&#xff08;或欺诈者&#xff09;行为发生变化并且您的训练…
阅读更多...
服务器部署—部署springboot之Linux服务器安装jdk和tomcat【建议收藏】

服务器部署—部署springboot之Linux服务器安装jdk和tomcat【建议收藏】

我是用的xshell连接的云服务器&#xff0c;今天想在服务器上面部署一个前后端分离【springbootvue】项目&#xff0c;打开我的云服务器才发现&#xff0c;过期了&#xff0c;然后又买了一个&#xff0c;里面环境啥都没有&#xff0c;正好出一期教程&#xff0c;方便大家也方便自…
阅读更多...
大数据框架之Hadoop：MapReduce（三）MapReduce框架原理——ReduceTask工作机制

大数据框架之Hadoop：MapReduce（三）MapReduce框架原理——ReduceTask工作机制

1、ReduceTask工作机制 ReduceTask工作机制&#xff0c;如下图所示。 &#xff08;1&#xff09;Copy阶段&#xff1a;ReduceTask从各个MapTask上远程拷贝一片数据&#xff0c;并针对某一片数据&#xff0c;如果其大小超过一定阈值&#xff0c;则写到磁盘上&#xff0c;否则直…
阅读更多...
DHTMLX Suite 8.0.0 Crack

DHTMLX Suite 8.0.0 Crack

适用于现代 Web 应用程序的强大 JavaScript 小部件库 - DHTMLX 套件 用于创建现代用户界面的轻量级、快速且通用的 JavaScript/HTML5 UI 小部件库。 DHTMLX Suite 有助于推进 Web 开发和构建具有丰富功能的数据密集型应用程序。 DHTMLX Suite 是一个 UI 小部件库&#xff0c;用…
阅读更多...
指针数组和数组指针的区别

指针数组和数组指针的区别

数组指针&#xff08;也称行指针&#xff09;定义 int (*p)[n];()优先级高&#xff0c;首先说明p是一个指针&#xff0c;指向一个整型的一维数组&#xff0c;这个一维数组的长度是n&#xff0c;也可以说是p的步长。也就是说执行p1时&#xff0c;p要跨过n个整型数据的长度。如要…
阅读更多...
【前端】JavaScript构造函数

【前端】JavaScript构造函数

文章目录概念执行过程返回值原型与constructor继承方式原型链其他继承方式&#xff08;还没写&#xff09;参考概念 在JS中&#xff0c;通过new来实例化对象的函数叫构造函数。实例化对象&#xff0c;也就是初始化一个实例对象。构造函数一般首字母大写。 构造函数的目的&…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023