题目描述
如题,已知一个数列,你需要进行下面三种操作:
-
将某区间每一个数乘上 x x x
-
将某区间每一个数加上 x x x
-
求出某区间每一个数的和
输入格式
第一行包含三个整数 n , m , p n,m,p n,m,p,分别表示该数列数字的个数、操作的总个数和模数。
第二行包含 n n n 个用空格分隔的整数,其中第 i i i 个数字表示数列第 i i i 项的初始值。
接下来 m m m 行每行包含若干个整数,表示一个操作,具体如下:
操作
1
1
1: 格式:1 x y k 含义:将区间
[
x
,
y
]
[x,y]
[x,y] 内每个数乘上
k
k
k
操作
2
2
2: 格式:2 x y k 含义:将区间
[
x
,
y
]
[x,y]
[x,y] 内每个数加上
k
k
k
操作
3
3
3: 格式:3 x y 含义:输出区间
[
x
,
y
]
[x,y]
[x,y] 内每个数的和对
p
p
p 取模所得的结果
输出格式
输出包含若干行整数,即为所有操作 3 3 3 的结果。
样例 #1
样例输入 #1
5 5 38
1 5 4 2 3
2 1 4 1
3 2 5
1 2 4 2
2 3 5 5
3 1 4
样例输出 #1
17
2
提示
【数据范围】
对于
30
%
30\%
30% 的数据:
n
≤
8
n \le 8
n≤8,
m
≤
10
m \le 10
m≤10
对于
70
%
70\%
70% 的数据:$n \le 10^3
,
,
, m \le 10^4$
对于
100
%
100\%
100% 的数据:$ n \le 10^5
,
,
, m \le 10^5$
除样例外, p = 571373 p = 571373 p=571373
(数据已经过加强qwq)
样例说明:
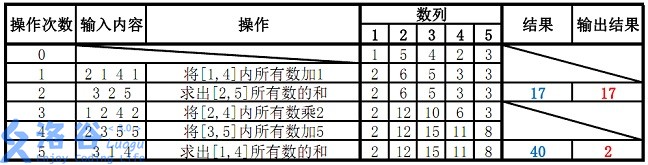
故输出应为 17 17 17、 2 2 2( 40 m o d 38 = 2 40 \bmod 38 = 2 40mod38=2 )
解题思路:
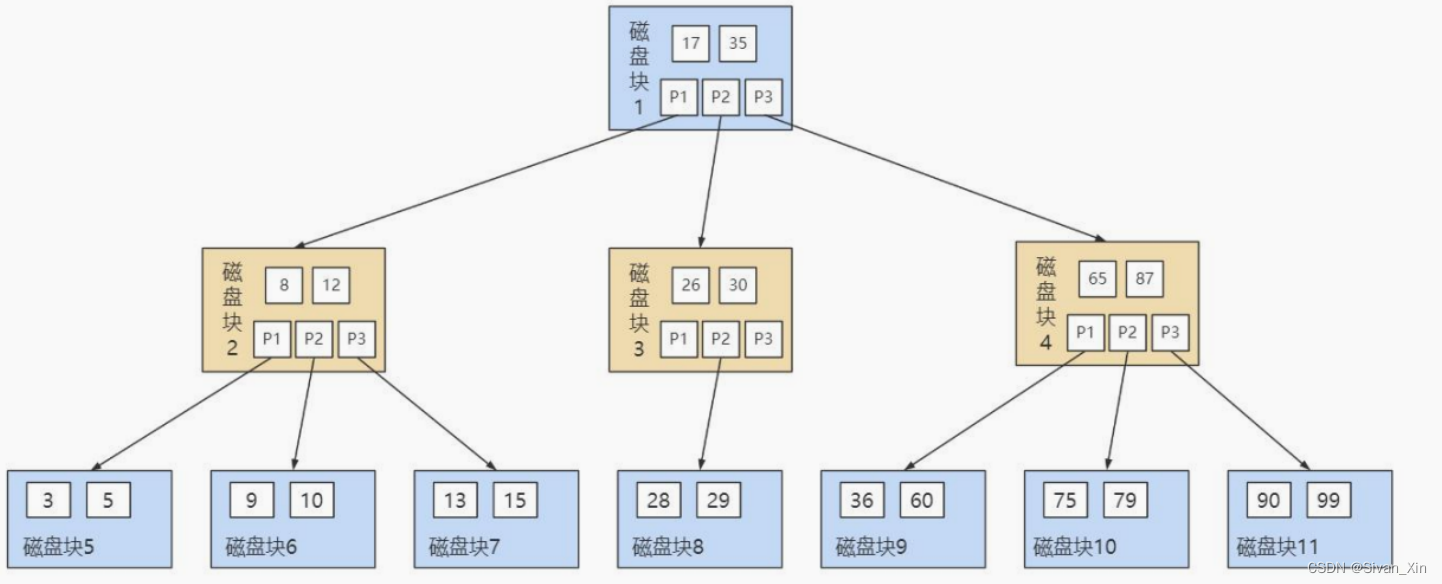
关于线段树,这里简单说明一下
首先是线段树的结构,因为用指针存储树的结构过于麻烦,所以用数组进行树的结构存储
初始化,为根节点分配索引 1 1 1
设根节点索引为root,左子树索引为left,右子树索引为right
则有left = root * 2,right = root * 2 + 1
然后你会发现每层最后一个节点的索引分别为 1 1 1、 3 3 3、 7 7 7、 15 15 15…
也就是 2 1 − 1 2^1-1 21−1、 2 2 − 1 2^2 - 1 22−1、 2 3 − 1 2^3 - 1 23−1、 2 4 − 1 2^4 - 1 24−1…,挺神奇的
所以我们为线段树维护的节点数量为区间长度$ * 4$
关于节点的数据,每个节点维护一段数组区间
左子树和右子树各自维护根节点的一半区间
维护的可以是区间的最大/最小值、区间和等
然后关于线段树的三大操作:建立、更新、查询,这里不详细展开
其核心思路就是先不断向下搜索确定子节点,然后递归更新根节点
如果直接看代码不太懂的话,一会我会推荐一篇我认为写得很好的算法说明
最后是比较难懂的懒惰标记(就是代码中的mul_tag和add_tag)
它的功能就是像名字一样,是用来偷懒的
更新到某个节点(该节点维护的区间为更新区间的真子集)之后停止更新,而是打上标记
如果之后需要用到它的子节点,那么就继续更新,这样可以减少操作量,提高效率
生动形象的话就是“工作你检查到哪里我就做到哪里”
这里是一个讲解的非常好的线段树说明(我就是从这里学的):线段树
本题有点难是因为有两个懒惰标记:加法标记和乘法标记
我们需要确定更新子树的时候这两个标记的操作顺序
从而决定这两个标记本身的更新顺序
比较简单的是先乘法后加法的顺序更新子树,先加后乘可以自行尝试
如果是操作 1 1 1,那么将两个标记同时乘上操作数即可
如果是操作 2 2 2,只需要把加法标记加上操作数,甚至不需要更新乘法标记
这里需要注意的一点是所有乘法标记最开始需要初始化为 1 1 1
但是在运算过程中,由于取模操作,乘法标记可能为 0 0 0
所以,懒惰标记是否传递的判断应该是mul_tag != 1
其余判断均会导致一些更新错误
那么,AC代码如下
#include <iostream>
using namespace std;
const int max_n = int(1e5);
const int max_m = int(1e5);
int n, m;
long long p;
long long num_arr[max_n + 1];
long long tree[max_n * 4 + 1];
long long mul_tag[max_n * 4 + 1];
long long add_tag[max_n * 4 + 1];
void push_down(int index, int l, int r) {
if (mul_tag[index] != 1 || add_tag[index]) {
long long mul = mul_tag[index];
long long add = add_tag[index];
int m = l + ((r - l) >> 1);
tree[index << 1] = ((tree[index << 1] * mul) + add * (long long)(m - l + 1)) % p;
mul_tag[index << 1] = (mul * mul_tag[index << 1]) % p;
add_tag[index << 1] = (add + add_tag[index << 1] * mul) % p;
tree[(index << 1) + 1] = ((tree[(index << 1) + 1] * mul) + add * (long long)(r - m)) % p;
mul_tag[(index << 1) + 1] = (mul * mul_tag[(index << 1) + 1]) % p;
add_tag[(index << 1) + 1] = (add + add_tag[(index << 1) + 1] * mul) % p;
mul_tag[index] = 1;
add_tag[index] = 0;
}
}
void build_tree(int index, int l, int r) {
if (l == r) {
tree[index] = num_arr[l] % p;
return;
}
else {
int m = l + ((r - l) >> 1);
build_tree(index << 1, l, m);
build_tree((index << 1) + 1, m + 1, r);
tree[index] = (tree[index << 1] + tree[(index << 1) + 1]) % p;
}
}
void update_1(int index, int l, int r, const long long mul, const int L, const int R) {
if (L <= l && r <= R) {
tree[index] = (mul * tree[index]) % p;
mul_tag[index] = (mul * mul_tag[index]) % p;
add_tag[index] = (mul * add_tag[index]) % p;
return;
}
else {
push_down(index, l, r);
int m = l + ((r - l) >> 1);
if (L <= m)
update_1(index << 1, l, m, mul, L, R);
if (m + 1 <= R)
update_1((index << 1) + 1, m + 1, r, mul, L, R);
tree[index] = (tree[index << 1] + tree[(index << 1) + 1]) % p;
}
}
void update_2(int index, int l, int r, const long long add, const int L, const int R) {
if (L <= l && r <= R) {
tree[index] = ((long long)(r - l + 1) * add + tree[index]) % p;
add_tag[index] = (add_tag[index] + add) % p;
return;
}
else {
push_down(index, l, r);
int m = l + ((r - l) >> 1);
if (L <= m)
update_2(index << 1, l, m, add, L, R);
if (m + 1 <= R)
update_2((index << 1) + 1, m + 1, r, add, L, R);
tree[index] = (tree[index << 1] + tree[(index << 1) + 1]) % p;
}
}
long long search(int index, int l, int r, const int L, const int R) {
if (L <= l && r <= R) {
return tree[index];
}
else {
push_down(index, l, r);
int m = l + ((r - l) >> 1);
long long left_ret = 0, right_ret = 0;
if (L <= m)
left_ret = search(index << 1, l, m, L, R);
if (m + 1 <= R)
right_ret = search((index << 1) + 1, m + 1, r, L, R);
return (left_ret + right_ret) % p;
}
}
int main() {
for (int i = 1; i <= max_n * 4; i++) mul_tag[i] = 1;
cin >> n >> m >> p;
for (int i = 1; i <= n; i++) cin >> num_arr[i];
build_tree(1, 1, n);
int q[3];
long long num;
for (int i = 1; i <= m; i++) {
cin >> q[0];
if (q[0] == 1) {
cin >> q[1] >> q[2] >> num;
update_1(1, 1, n, num % p, q[1], q[2]);
}
else if (q[0] == 2) {
cin >> q[1] >> q[2] >> num;
update_2(1, 1, n, num % p, q[1], q[2]);
}
else {
cin >> q[1] >> q[2];
cout << search(1, 1, n, q[1], q[2]) << endl;
}
}
return 0;
}