索引常见面试题

什么是索引

• 索引就是帮助存储引擎快速获取数据的一种数据结构，形象的说就是索引是数据的目录。
• 存储引擎，说白了就是如何为存储的数据建立索引、如何更新、查询数据等技术的实现方法。索引和数据就是位于存储引擎。

索引的分类

• 按「数据结构」分类：B+tree索引、Hash索引、Full-text索引。
  • InnoDB 存储引擎一定会为表创建一个聚簇索引，创建的聚簇索引或者二级索引默认使用的都是 B+Tree 这种数据结构。
  • B+Tree 存储千万级数据只需要 3-4 层高度就可以满足，从千万级的表查询目标数据最多需要 3-4 次磁盘 I/O。
  • 回表就是先检索二级索引，找到叶子节点（最底层的节点）获取主键值，然后通过聚簇索引中的B+Tree 树查询到对应的叶子节点，也就是要查两个 B+Tree 才能查到数据。
  • 索引覆盖就是当查询的数据是主键值时，因为只在二级索引就能查询到，不用再去聚簇索引查，就表示发生了索引覆盖，也就是只需要查一个 B+Tree就能找到数据。
• 按「存储类型」分类：聚簇索引（主键索引）、二级索引（辅助索引）。术语“聚簇”表示数据行和相邻的键值聚簇地存储在一起。这也形象地说明了聚簇索引叶子节点的特点，保存表的完整数据。
  • 聚簇索引的 B+Tree 的叶子节点存放的是实际数据，是表的所有完整数据。
  • 二级索引的 B+Tree 的叶子节点存放的是主键值，而不是实际数据。
• 按「字段特性」分类：主键索引、唯一索引、普通索引、前缀索引。
  • 主键索引也叫聚簇索引，就是建立在主键字段上的索引（叶子节点按照主键大小排序），在创建表的时候一起创建，一张表最多只有一个主键索引，索引列的值不允许有空值。
  • 唯一索引建立在 UNIQUE 字段上的索引，表示索引列的值必须唯一，允许有空值。但一张表可以有多个唯一索引。
  • 普通索引就是建立在普通字段上的索引，既不要求字段为主键，也不要求字段为 UNIQUE。
  • 前缀索引是指对字符类型字段的前几个字符建立的索引。使用前缀索引的目的是为了减少索引占用的存储空间，提升查询效率。
• 按「字段个数」分类：单列索引、联合索引。
  • 通过将多个字段组合成一个索引，该索引就被称为联合索引。
  • 联合索引按照最左匹配原则，如果创建了一个 (a, b, c) 联合索引，查询条件存在a就可以匹配上联合索引，比如where a=1；
    • 联合索引的最左匹配原则会一直向右匹配直到遇到范围查询（>、<）就会停止匹配。也就是范围查询的字段可以用到联合索引，但是在范围查询字段之后的字段无法用到联合索引。注意，对于 >=、<=、BETWEEN、like 前缀匹配的范围查询，并不会停止匹配。
  • 索引下推优化 （index condition pushdown) ，可以在联合索引遍历过程中，对联合索引中包含的字段先做判断，直接过滤掉不满足条件的记录，从而减少回表次数。
  • 实际开发工作中在建立联合索引时，建议把区分度大的字段排在前面，区分度越大，搜索的记录越少。 UUID 这类字段就比较适合做索引或排在联合索引列的靠前的位置。
    • 比如，性别的区分度就很小，字段的值分布均匀，那么无论搜索哪个值都可能得到一半的数据。

什么时候需要 / 不需要创建索引？

• 索引的缺点

  • 需要占用物理空间，数量越多，占用空间越大；
  • 创建、维护索引要耗费时间，这种时间随着数据量的增加而增大；
  • 会降低表的增删改的效率，B+ 树为了维护索引有序性，增删改时需要进行动态维护。

• 什么时候适用索引？

  • 字段有唯一性限制，比如商品编码。
  • 经常用于 WHERE 查询条件的字段，这样能够提高整个表的查询速度。如果查询条件不是一个字段，可以使用CREATE INDEX等语句建立联合索引。
  • 经常用于 GROUP BY 和 ORDER BY 的字段，这样在查询的时候就不需要再去做一次排序了，因为我们都已经知道了建立索引之后在 B+Tree 中的记录都是排序好的。

• 什么时候不需要创建索引？

  • WHERE 条件，GROUP BY，ORDER BY 里用不到的字段，索引的价值是快速定位，如果起不到定位作用的字段不需要创建索引。
  • 字段中存在大量重复数据，不需要创建索引，MySQL 有一个查询优化器，查询优化器发现某个值出现在表的数据行中的百分比很高的时候，它一般会忽略索引，进行全表扫描。
  • 表数据太少的时候，不需要创建索引。
  • 经常更新的字段不用创建索引，因为索引字段频繁修改，由于要维护 B+Tree的有序性，那么就需要频繁的重建索引，影响数据库性能。

有什么优化索引的方法？

• 前缀索引优化：使用某个字段中字符串的前几个字符建立索引。可以减小索引字段大小，节省空间。可以增加一个索引页存储前缀索引值，从而提高索引查询速度。
  • 但前缀索引有一定的局限性
    • order by 就无法使用前缀索引，因为前缀字符无法排序。
    • 无法把前缀索引用作覆盖索引，一般只有查询主键值时会用到覆盖索引。
• 覆盖索引优化：SQL 中查询的所有字段，都能从二级索引中查询得到记录，而不需要通过聚簇索引查询整行记录的所有信息，可以避免回表的操作。
• 主键索引最好是自增的：如果我们使用主键自增，那么每次插入的新数据就会按顺序添加到当前索引节点的位置，不需要移动已有的数据，当页面写满，就会自动开辟一个新页面。这种插入数据的方法效率非常高。
  • 如果我们使用非自增主键，可能产生页分裂。页分裂还有可能会造成大量的内存碎片，导致索引结构不紧凑，从而影响查询效率。
• 索引列最好设置为NOT NULL约束：
  • 第一原因：索引列存在 NULL 就会导致优化器在做索引选择的时候更加复杂，更加难以优化，因为可为 NULL 的列会使索引、索引统计、值的比较，都更复杂。比如进行索引统计时，count 会省略值为NULL 的行。
  • 第二个原因：NULL 值是一个没意义的值，但是它会占用物理空间。

从数据页的角度看B + 树

InnoDB是如何存储数据的？

• InnoDB的数据是按照数据页为单位来读写的，默认的大小是16KB。
• 数据页由七个部分组成：文件头（File Header）、页头（Page Header）、用户空间（UserRecords） 、最大、最小记录（Infimum + Supermum）、空闲空间（Free + Space）、页目录（PageDirectory）、文件尾（File Trailer）。
• 数据页中的文件头有两个指针，分别指向上一个和下一个数据页，连接起来的数据页相当于一个双向链表。实现逻辑上的连续存储。数据页中的记录按照主键的顺序组成单向链表。
• 页目录起到数据的索引作用。页目录由多个槽组成，**槽相当于分组数据的索引。**我们通过槽查找记录时，可以使用二分法快速定位要查询的记录在哪个槽（哪个记录分组），定位到槽后，再遍历槽内的所有记录，找到对应的记录，槽对应的值都是这个组的主键最大的记录。
• 在页的 7 个组成部分中，我们自己存储的记录会按照我们指定的行格式存储到 用户空间（User Records） 部分。一开始生成页的时候，并没有这个部分，每当我们插入一条记录，都会从 Free Space 部分申请一个记录大小的空间划分到User Records部分。当 Free Space 部分的空间全部被 User Records 部分替代掉之后，也就意味着这个页使用完了，如果还有新的记录插入的话，就需要去申请新的页了。

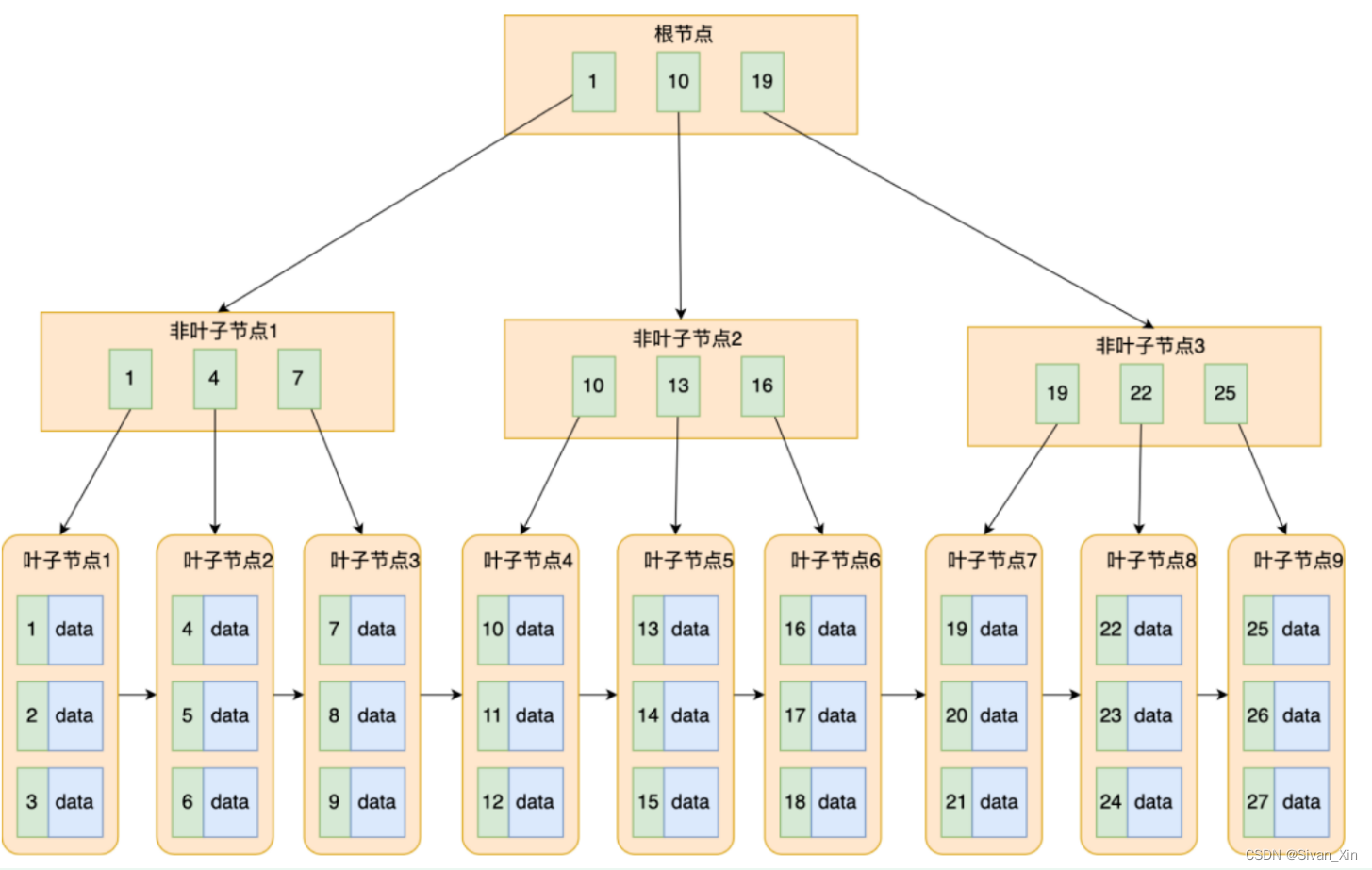
B + 树是如何进行查询的？

• B + 树的每个节点都是一个数据页。B + 树只有叶子节点才会存放数据，非叶子节点仅用来存放目录项作为索引。所有节点按照索引键大小排序，构成双向链表，便于范围查找。

• 定位记录所在哪一个页时，B + 树通过二分法快速定位到包含该记录的页。定位到该页后，又会在该页内进行二分法快速定位记录所在的分组（槽号），最后在分组内进行遍历查找。

• B + Tree索引又可以分成聚簇索引和二级索引（非聚簇索引），它们区别就在于叶子节点存放的是什么数据

  • 聚簇索引的叶子节点存放的是实际数据，所有完整的用户记录都存放在聚簇索引的叶子节点。

    • 因为表的数据都是存放在聚簇索引的叶子节点里，所以 InnoDB 存储引擎一定会为表创建一个聚簇索引，且由于数据在物理上只会保存一份，所以聚簇索引只能有一个。
    • InnoDB 在创建聚簇索引时，会根据不同的场景选择不同的列作为索引：
      • 如果有主键，默认会使用主键作为聚簇索引的索引键；
      • 如果没有主键，就选择第一个不包含 NULL 值的唯一列作为聚簇索引的索引键；
      • 在上面两个都没有的情况下，InnoDB 将自动生成一个隐式自增 id 列作为聚簇索引的索引键；

  • 由于一张表只能有一个聚簇索引，为了实现非主键字段的快速搜索，就引出了二级索引（非聚簇索引/辅助索引），它也是利用了 B+ 树的数据结构，但是二级索引的叶子节点存放的是主键值，不是实际数据。

为什么MySQL采用B + 树作为索引？

MySQL 默认的存储引擎 InnoDB 采用的是 B+ 树作为索引的数据结构，原因有如下几点：

• B+ 树的非叶子节点仅存放索引，因此数据量相同的情况下，相比既存索引又存记录的 B 树，B+树的非叶子节点可以存放更多的索引，因此 B+ 树可以比 B 树更「矮胖」，查询底层节点的磁盘 I/O次数会更少。
• B+ 树有大量的冗余节点（所有非叶子节点都是冗余索引），这些冗余索引让 B+ 树在插入、删除的效率都更高，比如删除根节点的时候，不会像 B 树那样会发生复杂的树的变化；
• B+ 树叶子节点之间用双向链表连接，既能向右遍历，也能向左遍历，有利于范围查询，而 B 树要实现范围查询，因此只能通过树的遍历来完成范围查询，这会涉及多个节点的磁盘 I/O 操作，范围查询效率不如 B+ 树。

怎样的索引的数据结构是好的？

• MySQL的数据是持久化的，保存在磁盘上。磁盘读写的最小单位是扇区，扇区只有512B大小，操作系统会读写多个扇区，最小的读取单位是块。Linux中块的大小为4KB，也就是8个扇区。由于数据库的索引是保存在磁盘上的，所以查询数据时，要先读取索引到内存，通过索引找到磁盘中的某行数据，然后读入到内存，I/O操作次数越多，所消耗的时间也越大。所以设计MySQL索引的数据结构时，要尽可能减少磁盘I/O次数，并且能够高效地查找某一个记录，也要能高效的范围查找。
• 为什么不用二分查找树？
  • 二叉查找树的特点是一个节点的左子树的所有节点都小于这个节点，右子树的所有节点都大于这个节点，二叉查找树的搜索速度块，解决了插入新节点的问题，但是当每次插入的元素都是二叉查找树中最大的元素，二叉查找树就会退化成了一条链表，查找数据的时间复杂度变成了 O(n)。随着元素插入越多，树的高度越高，磁盘IO操作也就越多，查询性能严重下降。
• 为什么不用自平衡二叉树（AVL树）？
  • 自平衡二叉树在二叉查找树的基础上增加了一些条件约束：每个节点的左子树和右子树的高度差不能超过 1。但是随着插入的元素变多，会导致树的高度变高，磁盘IO操作次数就会变多，影响整体数据查询效率。
• 为什么不用B树？
  • B树解决了树的高度问题，但是B树的每个节点都包含数据（索引+记录），而用户记录的数据大小有可能远远超过索引数据，就要花费更多的IO来读取到有用的索引数据。
• B + 树对B树进行了升级，与B树的区别主要是以下几点
  • 叶子节点（最底部的节点）才会存放实际数据（索引+记录），非叶子节点只会存放索引；
  • 所有索引都会在叶子节点出现，叶子节点之间构成一个有序链表，对范围查找非常有帮助；
  • 非叶子节点的索引也会同时存在在子节点中，并且是在子节点中所有索引的最大（或最小）。
  • 非叶子节点中有多少个子节点，就有多少个索引；

MySQL中的B + 树

• Innodb 使用的 B+ 树有一些特别的点，比如：
  • B+ 树的叶子节点之间是用「双向链表」进行连接，这样的好处是既能向右遍历，也能向左遍历。
  • B+ 树节点的内容是数据页，数据页里存放了用户的记录以及各种信息，每个数据页默认大小是 16 KB。
• Innodb 根据索引类型不同，还分为聚集和二级索引。他们的共同点是都使用B + 树这种数据结构。他们区别在于，聚簇索引的叶子节点存放的是实际数据，所有完整的用户记录都存放在聚集索引的叶子节点，而二级索引的叶子节点存放的是主键值。

补充：

• B+树

  一个m阶的B+树具有如下特征：

  • 有k个子树的中间节点包含有k个元素（B树中是k-1个元素），每个元素不保存数据，只用来索引，所有数据都保存在叶子节点。
  • 所有的叶子结点中包含了全部元素的信息，及指向含这些元素记录的指针，且叶子结点本身依关键字的大小自小而大顺序链接。
  • 所有的中间节点元素都同时存在于子节点，在子节点元素中是最大（或最小）元素。

• B树

  一个 M 阶的 B 树（M>2）有以下的特性：

  • 根节点的儿子数的范围是 [2,M]。
  • 每个中间节点包含 k-1 个关键字和 k 个孩子，孩子的数量 = 关键字的数量 +1，k 的取值范围为[ceil(M/2), M]。
  • 叶子节点包括 k-1 个关键字（叶子节点没有孩子），k 的取值范围为 [ceil(M/2), M]。
  • 假设中间节点节点的关键字为：Key[1], Key[2], …, Key[k-1]，且关键字按照升序排序，即 Key[i]<Key[i+1]。此时 k-1 个关键字相当于划分了 k 个范围，也就是对应着 k 个指针，即为：P[1], P[2], …,P[k]，其中 P[1] 指向关键字小于 Key[1] 的子树，P[i] 指向关键字属于 (Key[i-1], Key[i]) 的子树，P[k]指向关键字大于 Key[k-1] 的子树。

  

MySQL单表不要超过2000W行，靠谱吗？

• InnoDB存储引擎的表数据时存放在一个.idb(innodb data)的文件中，也叫做表空间。
• MySQL 的表数据是以页的形式存放的，页在磁盘中不一定是连续的。页的空间是 16K, 但并不是所有的空间都是用来存放数据的，会有一些固定的信息，如，页头，页尾，页码，校验码等等。
• 在 B+ 树中，叶子节点和非叶子节点的数据结构是一样的，区别在于，叶子节点存放的是实际的行数据，而非叶子节点存放的是主键和页号。
• 索引结构不会影响单表最大行数，2000W 也只是推荐值，超过了这个值可能会导致 B + 树层级更高，影响查询性能。

索引失效有哪些？

• 当我们使用左或者左右模糊匹配的时候，也就是 like %xx 或者 like %xx% 这两种方式都会造成索引失效。
  • 因为索引 B+ 树是按照「索引值」有序排列存储的，只能根据前缀进行比较。
• 对索引列进行表达式计算、使用函数，这些情况下都会造成索引失效。
  • 因为索引保存的是索引字段的原始值，而不是经过计算后的值。
• 索引列发生隐式类型转换。MySQL 在遇到字符串和数字比较的时候，会自动把字符串转为数字，然后再进行比较。如果字符串是索引列，而输入的参数是数字的话，那么索引列会发生隐式类型转换。
  • 由于隐式类型转换是通过 CAST 函数实现的，等同于对索引列使用了函数，所以就会导致索引失效。
• 联合索引没有遵循最左匹配原则，也就是按照最左边的索引优先的方式进行索引的匹配，就会导致索引失效。
• 在 WHERE 子句中，如果在 OR 前的条件列是索引列，而在 OR 后的条件列不是索引列，那么索引会失效。
  • 因为 OR 的含义就是两个只要满足一个即可，只要有条件列不是索引列，就会进行全表扫描。

MySQL使用like “%x”，索引一定会失效吗？

• 使用左模糊匹配（like “%xx”）并不一定会走全表扫描（索引不一定失效），如果数据库表中的字段只有主键+二级索引，那么即使使用了左模糊匹配，也不会走全表扫描（type=all），而是走全扫描二级索引树(type=index)。

• 联合索引要遵循最左匹配才能走索引，但是如果数据库表中的字段都是索引的话，即使查询过程中，没有遵循最左匹配原则，也是走全扫描二级索引树(type=index)。

count（*）和count（1）有什么区别？哪个性能好？

• 性能：count(*) = count(1) > count(主键字段) > count(字段)

• count()是什么？

  • count()是一个聚合函数，函数的参数不仅可以是字段名，也可以是其他任意的表达式，作用是统计符合查询条件的记录中，函数指定的参数不为 NULL 的记录有多少个。
  • 比如count(name)：统计name不为NULL的字段有多少。count(1)：统计1不为NULL的字段有多少。1永远不可能是NULL，所以其实是在统计一共有多少条记录。

• count(主键字段)执行过程是怎样的？

  • 如果表中只有主键索引，没有二级索引，InnoDB在遍历时就会遍历聚簇索引，将读取到的记录返回给server层（server层维护了一个count的变量），然后读取记录中的主键值，如果为NULL，就将count变量 + 1。如果表中有二级索引，InnoDB就会遍历二级索引。

• count(1)执行过程是怎样的？

  • 如果表中只有主键索引，没有二级索引，InnoDB遍历时会遍历聚簇索引，将读取到的记录返回给server层，但是不会读取记录中的任何字段的值。因为 count 函数的参数是 1，不是字段，所以不需要读取记录中的字段值。如果表中有二级索引，InnoDB就会遍历二级索引。
    • 因为 count 函数的参数是 1，不是字段，所以不需要读取记录中的字段值。

• count(*)执行过程是怎样的？

  • count(*) 其实等于 count(0)，也就是说，当你使用 count(*) 时，MySQL 会将 * 参数转化为参数 0 来处理。

• count(字段)执行过程是怎样的？

  • 会采用全表扫描的方式来计数，所以它的执行效率是比较差的。

• count(1)、 count(*)、 count(主键字段)在执行的时候，如果表里存在二级索引，优化器就会选择二级索引进行扫描。所以，如果要执行 count(1)、 count(*)、 count(主键字段) 时，尽量在数据表上建立二级索引，这样优化器会自动采用 key_len 最小的二级索引进行扫描，相比于扫描主键索引效率会高一些。

• 为什么要通过遍历的方式计数？

  • InnoDB 存储引擎是支持事务的，同一个时刻的多个查询，由于多版本并发控制（MVCC）的原因，InnoDB 表“应该返回多少行”也是不确定的，所以无法像 MyISAM一样，只维护一个 row_count 变量。

• 如何优化count(*) ？

  • 如果业务对于统计个数不需要很精确，可以使用explain 命令来进行估算。
  • 使用额外表保存计数值，将这个计数值保存到单独的一张计数表中。