题目描述：

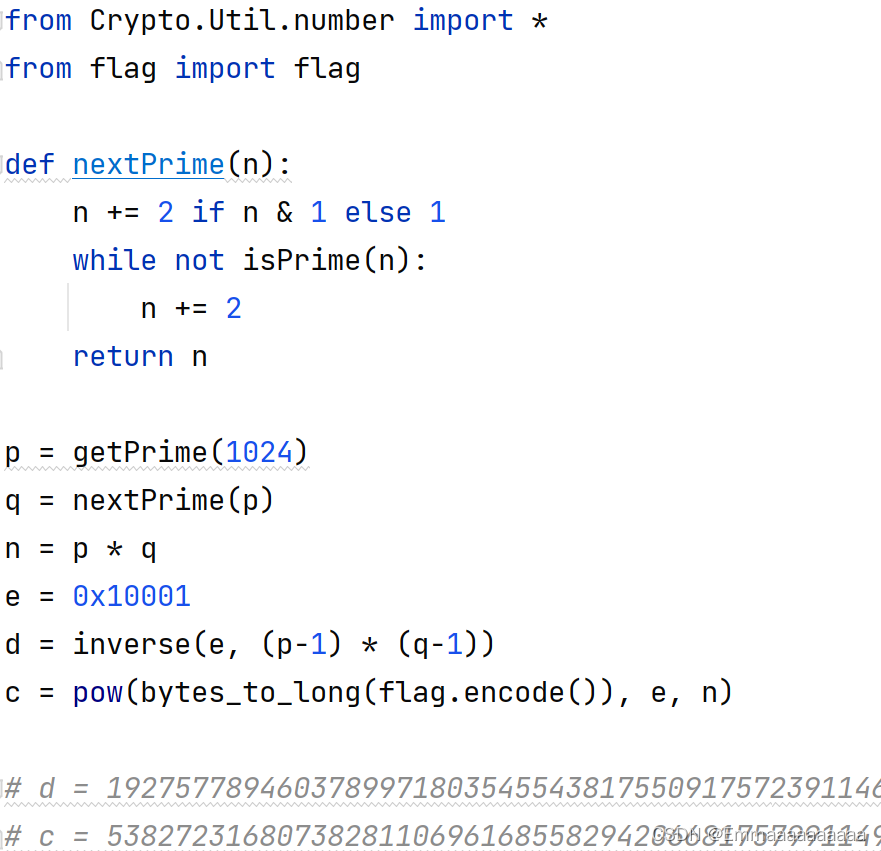
题目分析：

• 首先明确两个公式：

e*d = 1 mod (p-1)(q-1)
ed1 = e*d - 1 = k(p-1)(q-1)

• 想要解出此题，我们必须知道n,而要知道n,我们要知道p和q的值
• 通过 e*d 的计算，我们知道其长度为2066位，而生成p的条件为 getPrime(1024)，所以（p-1)（q-1）应该为2048位

此处所说的位数长度是以Bit为单位，加一减一都不影响位数，相乘的话即为位数相加，这些性质记住就好，以下是计算代码：

from Crypto.Util.number import *
e = 65537
d = 19275778946037899718035455438175509175723911466127462154506916564101519923603308900331427601983476886255849200332374081996442976307058597390881168155862238533018621944733299208108185814179466844504468163200369996564265921022888670062554504758512453217434777820468049494313818291727050400752551716550403647148197148884408264686846693842118387217753516963449753809860354047619256787869400297858568139700396567519469825398575103885487624463424429913017729585620877168171603444111464692841379661112075123399343270610272287865200880398193573260848268633461983435015031227070217852728240847398084414687146397303110709214913
print(gmpy2.bit_length(e*d))
# 2064
p = getPrime(1024)
print(gmpy2.bit_length(p))
# 1024
print(gmpy2.bit_length(p-1))
# 1024

• 又 ed1 = e*d - 1 = k(p-1)(q-1)，2064-2048 = 16，所以k值必在 pow(2,15)至pow(2,16)之间
• 所以，我们可以利用此条件暴力求解k值，从而求出(p-1)*(q-1),间接求出 p 和 q 的值
• 那如何间接法呢？
• 首先我们求得了(p-1)(q-1),而p和q是两个相邻的质数，所以我们可以使用sympy库对p,q进行求解。思路为先对(p-1)(q-1)开方，再求得大于开方所得数和小于开方所得数的质数

p = sympy.prevprime(gmpy2.iroot((e*d-1)//i,2)[0])
q = sympy.nextprime(p)

• 其中 sympy.prevprime(x)是求大于x最近的质数，sympy.nextprime(x)是求小于x最近的质数。
• 解题代码如下：

import gmpy2
from Crypto.Util.number import long_to_bytes
import sympy
# e = 0x10001
e = 65537
d = 19275778946037899718035455438175509175723911466127462154506916564101519923603308900331427601983476886255849200332374081996442976307058597390881168155862238533018621944733299208108185814179466844504468163200369996564265921022888670062554504758512453217434777820468049494313818291727050400752551716550403647148197148884408264686846693842118387217753516963449753809860354047619256787869400297858568139700396567519469825398575103885487624463424429913017729585620877168171603444111464692841379661112075123399343270610272287865200880398193573260848268633461983435015031227070217852728240847398084414687146397303110709214913
c = 5382723168073828110696168558294206681757991149022777821127563301413483223874527233300721180839298617076705685041174247415826157096583055069337393987892262764211225227035880754417457056723909135525244957935906902665679777101130111392780237502928656225705262431431953003520093932924375902111280077255205118217436744112064069429678632923259898627997145803892753989255615273140300021040654505901442787810653626524305706316663169341797205752938755590056568986738227803487467274114398257187962140796551136220532809687606867385639367743705527511680719955380746377631156468689844150878381460560990755652899449340045313521804
p = 0
q = 0

for k in range(pow(2,15),pow(2,16)):
    #  pow(x,y) ---> x 的 y 次方
    #  pow(x,y,z) ---> x 的 y 次方后，取余 z
    if (e*d-1)%k == 0:
        p = sympy.prevprime(gmpy2.iroot((e*d-1)//k,2)[0])
        # sympy.prevprime(x)是求大于x最近的质数
        # iroot(x,n) ---> x开n次根 ,返回值有两个，前一个是开方出来的整数部分，后一个是能否开出来，若能则为true,不能则为flase
        q = sympy.nextprime(p)
        # sympy.nextprime(x)是求小于x最近的质数
        if (p-1)*(q-1) == (e*d-1)//k:
            break

n = p*q
m = pow(c,d,n)
m1 = long_to_bytes(m)
print(m1)

• 最终得出 flag{70u2_nn47h_14_v3ry_gOO0000000d}

收获与体会：

• 了解了一些字节的相关知识
• 知道了函数 sympy.prevprime(x)和sympy.nextprime(x)的相关知识
  sympy.prevprime(x)是求大于x最近的质数
  sympy.nextprime(x)是求小于x最近的质数
• 回顾了iroot(x,n) 和 pow(x,y) 的相关知识
  iroot(x,n) —> x开n次根 ,返回值有两个，前一个是开方出来的整数部分，后一个是能否开出来，若能则为true,不能则为flase
  pow(x,y) —> x 的 y 次方
  pow(x,y,z) —> x 的 y 次方后，取余 z