本文是我通过做题和借鉴一些前人总结的套路而得出的思路和方法,刚好这次CSDN第八周的周赛上出了三道动态规划的题目,我会结合题目对我的思路进行一个输出,会从最简单的一维dp开始讲解到二维dp,希望对你有帮助,有错误希望指出,一起进步~~
目录
一. 应用动态规划的三大步骤
1.1 定义数组元素的含义
1.2 最优子结构(数组元素之间的关系式)
1.3 找到初始值
二. 一维dp数组思路及解题
2.1 爬楼梯
2.2 最大子数组和
三. 二维dp数组思路及解题
3.1 不同路径
一. 应用动态规划的三大步骤
首先,我们先来说一下动态规划这个词,就是动态的去把一个规则去对应用的数据进行一个合理的划分。
就是利用历史数据,避免重复计算来对空间,时间复杂度进行一个更好的优化。而这些历史数据,我们一般要用一些变量来进行保存,一般我们用数组来保存,正常题目我们用一维数组或二维数组保存就可以了,更为复杂的情况我们就可以选用更高维度的数组进行保存,这得视情况而定。
1.1 定义数组元素的含义
首先上面也提到了我们会用一个数组来对历史数据进行一个保存,一般我们会用dp来进行一个命名,一维数组就是 dp[ ] 。
这时最重要的一点是,我们要搞清楚我们所定义的这个数组中的每一个元素代表的是什么,dp[0]……dp[i] 你是否都清楚是什么?
这个是我们做题的前提。dp[i]在每道题目都有每道题目的含义,搞懂我们才能进行下一步!!!
1.2 最优子结构(数组元素之间的关系式)
从定义上来说,最优子结构就是问题的最优解包含子问题的最优解。就是我们可以通过子问题的最优解,推导出问题的最优解的意思。
相信很多朋友会对定义上的最优子结构有困惑,但其实我们可以抛开这个名字来看,从我们每个动态规划所定义的数组dp来看!
其实我们就是要找出数组元素之间的关系式,或者说他们之间有什么递进关系,动态规划是有种归纳法的感觉的,我们的dp[i]总是会由我们的 dp[i-1],dp[i-2]……dp[1] 来进行推导得出的,这就是我们上面所讲的利用历史数据来推导出我们最新的dp值,所以我们要找出我们定义的数组dp中的元素之间的关系式。
这可以说是最关键的一步,也是最难的一步,一般只要花时间把关系式找出来了,题目也就迎刃而解了。
1.3 找到初始值
通过上面我们找到的数组元素之间的关系式,将公式推导最开始的时候,从dp[0]开始,求出第一种情况的公式,只要右边式子中除了我们求知的新的数组元素的值还有我们未知的元素时,我们都应该把公式继续往下推,找到那个所有元素都已知的公式,在此之前的元素你都需要判定是否可推,找出我们所需的初始值,将初始值进行一个直接的求解。
有了初始值,加上数组元素之间的关系式,我们就可以得到dp中所有的值,而dp中每个元素的含义都是由你自己所定义的, 你所需要求解的是什么,就应该定义它是什么,这样,求解出了dp,自然就求解出我们所要的解了。
要是感觉还是迷迷糊糊的,不慌,我带你从题目中来理解!
二. 一维dp数组思路及解题
2.1 爬楼梯
题目是力扣中的题,可以直接点过去进行尝试!
问题描述:
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬
1或2个台阶。你有多少种不同的方法可以爬到楼顶呢?
1)定义数组元素的含义
首先,我们观察问题,问的是我们要上 n 层台阶总共有多少种方法,那我们可以定义我们的 dp[n] 为第 n 层台阶的方法数,所以 dp[ i ] 的含义就是:跳上 i 层的台阶总共有 dp[i] 中跳法。
2)最优子结构(数组元素之间的关系式)
我们知道了dp[i]的含义后,对于这道题,我们可以知道每次只能爬 1 或 2 个台阶,所以在第n层,只有两种到达的方法,一种是从 n-1 层爬 1 个台阶上来,另一种就是从 n-2 层爬 2 个台阶,我们要求的是所有可能的爬法,所以我们可以得出,dp[n] = dp[n-1] + dp[n-2]。
3)找到初始值
首先观察得到的数组元素关系式,dp[n] = dp[n-1] + dp[n-2],我们知道数组的元素下标是不可以为负,最小从0开始的,所以第一个 dp[n-2] 就应该为 dp[0] 。
- dp[2] = dp[1] + dp[0] ,其中dp[1]、dp[0]都不是已得出的值,所以初始值中应该有dp[1]、dp[0],我们必须直接求出它们的数值,可以轻易得出dp[1] = 1,dp[0] = 0 (第 0 层是出发点肯定为 0 ,第 1 层只能上一步所以只有 1 种),此时应该回顾下dp[2]是否有可能通过题目条件直接得到,可以发现可以直接上两步到第 2 层,所以最后 dp[2] = dp[1] + dp[0] +dp[2]的初始值 = 2;
- dp[3] = dp[2] + dp[1],这次我们可以知道右边式子中 dp[1] 已经求出,dp[2]也已经推出了,所以右边式子是全部已知了,再检查下 dp[3] 是否可以通过题目条件直接得出,发现不可以,所以写代码时我们只需要把dp[1]、dp[0]、dp[2]作为初始值即可。
这题的初始值感觉和CCF-CSP真题《202203-1—未初始化警告》有点相像的,有兴趣的朋友可以去做一下这题。
4)代码实战
三个步骤都出来了,直接上代码进行实战一下,我采用的是python语言的自己输出输出的方法,方便想进行尝试的朋友进行测试调试:
# 输入一个n表示要上n层台阶(n我默认大于1了)
n = int(input())
# 创建出一个数组来保存历史数据
dp = [0]*(n+1)
# 将我们所需的初始值进行求值赋值
dp[0] = 0
dp[1] = 1
dp[2] = 2
# 通过关系型求出整个dp[n]
for i in range(3,n+1):
dp[i] = dp[i-1] + dp[i-2]
# 输出我们所求的上到第n层的方法数,即dp[n]
print(dp[n])这道题其实严谨来讲应该进行判断 n 的值,因为要是为1的话,初始值就不用到2了,但我们讲的是思路,就不吹毛求疵了。
2.2 最大子数组和
题目是力扣中的题,可以直接点过去进行尝试!
问题描述:
给你一个整数数组
nums,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。子数组 是数组中的一个连续部分。
1)定义数组元素的含义
首先,读题目过后我们知道要找出最大和的连续子数组,那我们可以想到在每个位置上都存入当前的最大和,最后就可以得到所有位置的最大和了。所以 dp[ i ] 的含义就是:在 i 位置时数组所能达到的最大和。
2)最优子结构(数组元素之间的关系式)
我们知道了 dp[i] 的含义后,对于这道题,我们要想的是每个位置应该怎么得到它的数组最大和。由于每个位置都是自己及之前的最大和,所有我们只要将 nums[ i ] 和 nums[ i ] + dp[i-1] 进行一个最大值比较就可以求出当前最大和了。
即 dp[ i ] = max( nums[ i ] , nums[ i ] + dp[ i-1 ])。
3)找到初始值
观察关系式,我们可以发现原数组的 nums[ i ] 就是我们所需的初始值,我们不用额外的去设置求出初始值。
4)代码实战
def maxSubArray(self, nums: List[int]) -> int:
# 设置一个初始的dp数组进行每个位置的最大和的存储
dp = [0]*len(nums)
# 遍历数组nums,通过数组关系式求出每个dp[i]的值
for i in range(len(nums)):
dp[i] = max(nums[i],dp[i-1]+nums[i])
# 返回的dp数组中的最大值就是具有最大和的连续子数组的和
return max(dp)三. 二维dp数组思路及解题
3.1 不同路径
老规矩,题目是力扣中的题,可以直接点过去进行尝试!
问题描述:
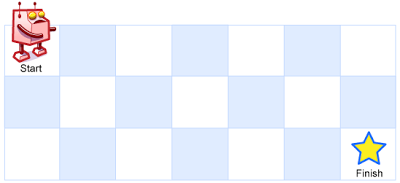
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?以下图为例进行解析:
1)定义数组元素的含义
首先,这道题是要求从左上角到右下角有多少条路径,所以很明显数组 dp[i] [j] 的含义为:当机器人从左上角走到(i, j) 这个位置时,一共有 dp[i] [j] 种路径。那么,dp[m-1] [n-1] 就是我们要的答案了。
注意:这个网格相当于一个二维数组,数组是从下标为 0 开始算起的,所以 右下角的位置是 (m-1, n - 1),所以 dp[m-1] [n-1] 就是我们要找的答案。
2)最优子结构(数组元素之间的关系式)
想象一下,我们在每个格子的来处只能是 左边一格向右走一步 或者是 上面一格向下走一步 ,所以每个格子的数组元素的关系式为: dp[i] [j] = dp[i-1] [j] + dp[i] [j-1]。
3)找到初始值
显然,当 dp[i] [j] 中,如果 i 或者 j 有一个为 0,那么还能使用关系式吗?答是不能的,因为这个时候把 i - 1 或者 j - 1,就变成负数了,数组就会出问题了,所以我们的初始值是计算出所有的 dp[0] [0….n-1] 和所有的 dp[0….m-1] [0]。这个还是非常容易计算的,相当于计算机图中的最上面一行和左边一列。因此初始值如下:
- dp[0] [0….n-1] = 1; // 相当于最上面一行,机器人只能一直往左走
- dp[0…m-1] [0] = 1; // 相当于最左面一列,机器人只能一直往下走
4)代码实战
def uniquePaths(self, m: int, n: int) -> int:
# 假如只有一行或者只有一列时
if m<=0 or n<=0:
return 1
# 设置一个dp数组存储每个位置的最多路径
dp = [[0]*n for _ in range(m)]
# 初始化第 0 行的路径为1
for i in range(m):
dp[i][0] = 1
# 初始化第 0 列的路径为1
for i in range(n):
dp[0][i] = 1
# 通过关系型动态规划每个位置的最多路径
for i in range(1,m):
for j in range(1,n):
dp[i][j] = dp[i-1][j]+dp[i][j-1]
# 输出右下角的最多路径
return dp[m-1][n-1]先写到这了,未完待续~~