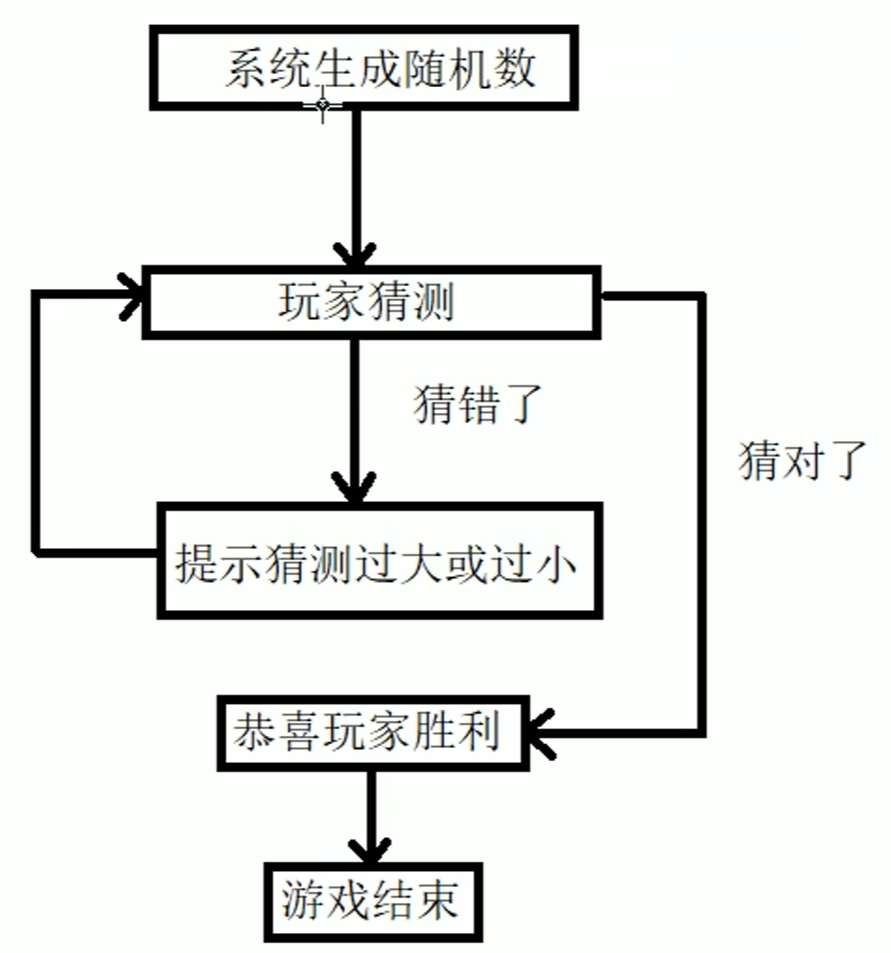
23、高自由度下的E类波形理论计算(附Matlab代码)
0、代码
任意占空比、电压导数条件下的E类波形与阻抗条件计算Matlab
注意修改路径,我这边是:!!!!!!!!!!!!!!!!!!!!
addpath(genpath(‘G:\WORKSPACE\MATLAB_WORKSPACE\06_FinalDesign_PA\00_ClassE’));
1、高自由度概述
此处高自由度指的是导通角可能为其他数值(不固定为50%),且并不严格满足0电压导数条件。
国内的文章对于E类的分析往往限定于占空比为50%且严格满足0电压导数条件(ZVDS)。但是在实际的设计中我们可能需要设计占空比为其他数值的E类功放(降低导通角能提高效率性能),或者需要亚正常模式(不严格满足ZVDS条件)下的E类功放以提升其带宽性能。例如一篇期刊文章:Analysis and design of continuous class-E power amplifier at sub-nominal condition就是放宽了其ZVDS条件从而实现了更大的带宽。
然而,在高自由状态下的E类波形应该是怎么样的呢,其实在60年前就有学者给出了计算的的公式(Idealized operation of the class_E tuned power amplifier),但是其计算比较复杂且涉及各种方程的求解,在此我对其进行了分析,并写成了Matlab代码的形式,大家只需要修改占空比参数和导数条件参数即可得到波形,为自己的分析助力。
2、理论推导的计算公式
原论文连接为:
Idealized operation of the class_E tuned power amplifier
求解的实质就是对二十几个微分和积分方程求解,因为是全变量的方程,此处我使用的是Matlab的syms和fsolve函数进行求解的。对求解过程不感兴趣的小伙伴可以跳过这一章节。
设计已知量:占空比相关参数y、电压导数参数ksi、电源电压Vcc、直流电流Idc、设计的输出功率P0。
此处从计算的角度进行论述:
step1:已知占空比相关参数y和电压导数参数ksi,计算输出电压相位phi:
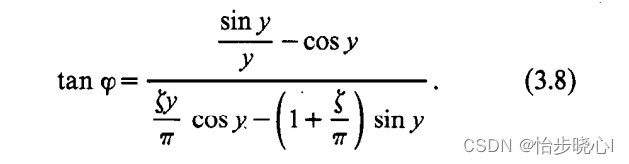
step2:由phi和y计算中间参数g(此处需要简单变换):
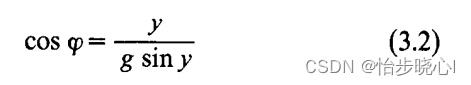
step3:根据下述公式计算负载电阻R,这边Rdc=Vcc/Idc也可以直接算出来:

step4:由上述计算得出的参数可以计算电容的容抗参数B:
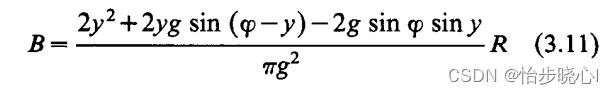
step5:由上述计算得出的参数可以计算参数q1、q2、q3,由此电感带来的相位移动也可以被计算出来:
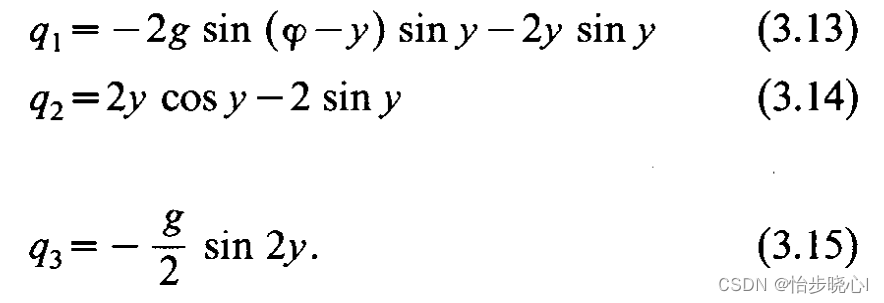
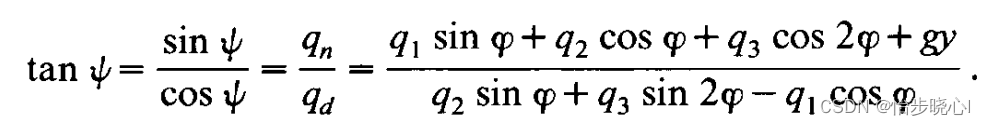
由此电感的感抗可以被计算
X=R.*tan(psi);
step6:计算电压和电流波形:
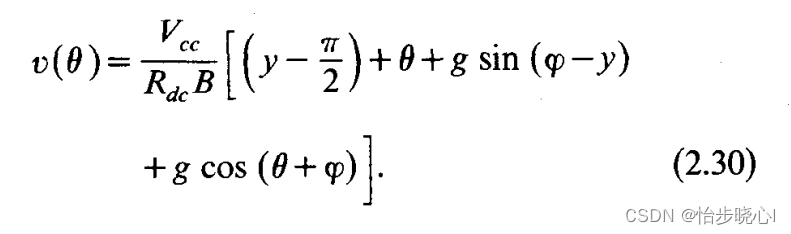
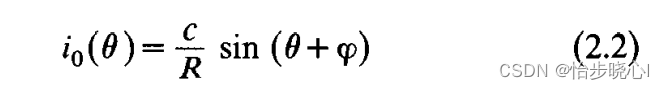
(电流如下计算!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!)
i(theta)=Idc-i0(theta)
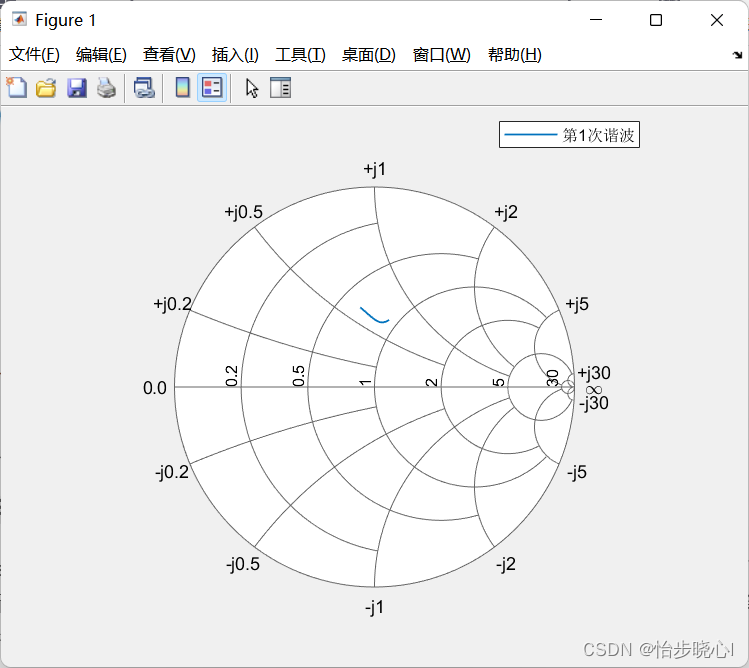
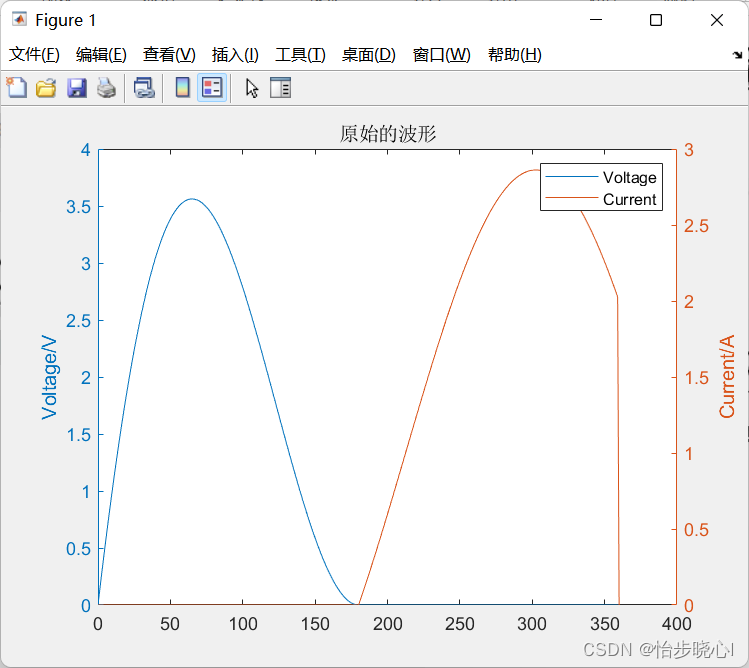
3、波形简单展示(运行classE_noSweep.m):
1、导通角180度、Ksi=0(即满足ZVDS条件)
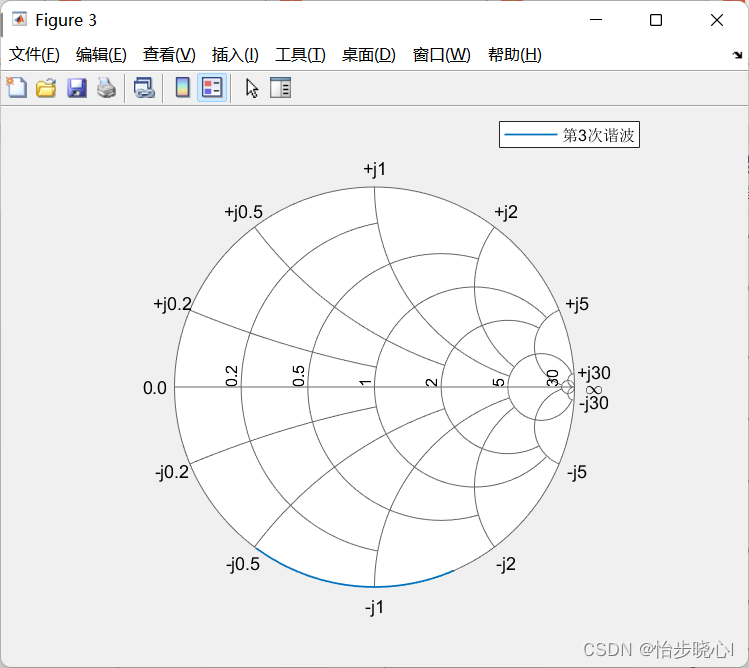
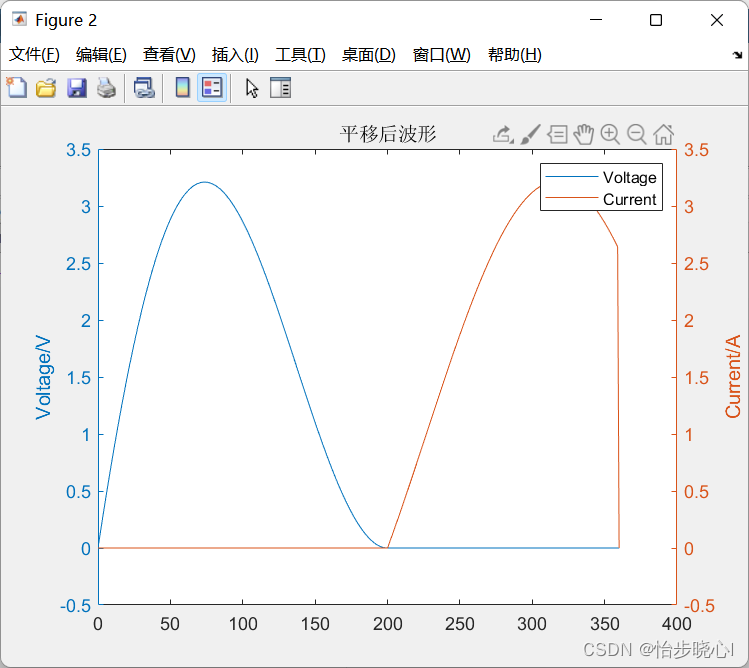
2、导通角160度、Ksi=0(即满足ZVDS条件)
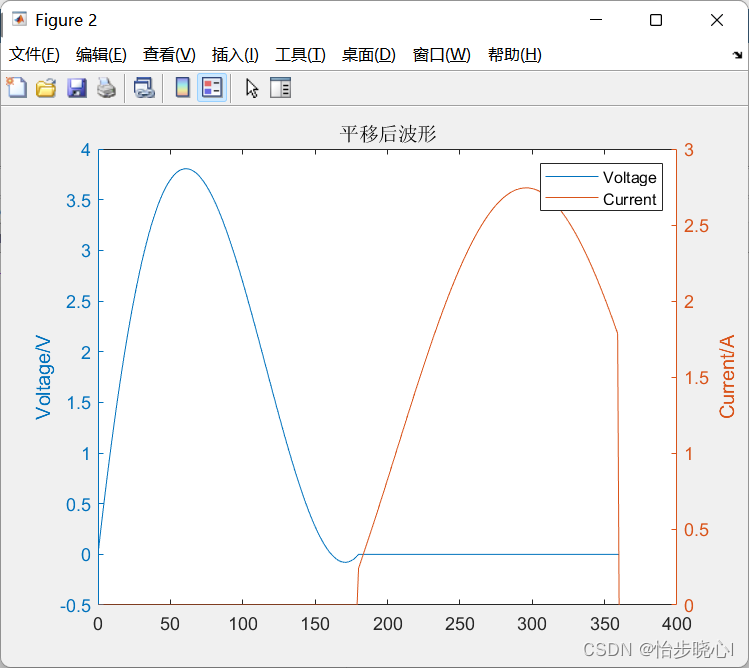
2、导通角180度、Ksi=1(即不满足ZVDS条件)
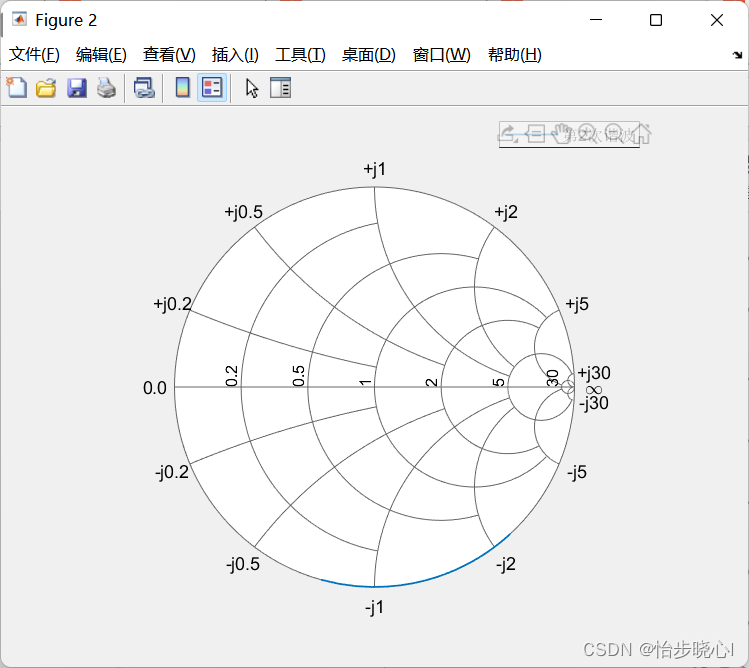
4、基于亚正常模式的E类宽带设计空间(运行classE_Sweepksi.m)
Analysis and design of continuous class-E power amplifier at sub-nominal condition就是放宽了其ZVDS条件从而实现了更大的带宽。但是它是从连续E类的角度分析的,对于普通的E类放宽了其ZVDS条件也能实现宽带:此处直接展示,放宽ksi条件为(-pi/2,pi/2)(运行classE_Sweepksi得到):