1 问题
我们在深度学习的过程中,我们学到了自适应池化、最大值池化和均值池化。那么,我们想要探究一下自适应池化、最大值池化和均值池化效率,哪一个更高?
2 方法
在之前的学习中,我们学到了自适应池化、最大值池化和均值池化,三种池化方式的运行速率的运行效率是如何的呢,我们使用对照实验将几种池化方式比较出来。
首先呢,我们先定义卷积层,直接转换输入的通道数:
conv = nn.Conv2d(
in_channels=1, # 输入为单通道灰度图
out_channels=128, # 输出为128通道img
kernel_size=3,
stride=1,
padding=1
) # [-, 16, 28, 28]
然后我们定义三种池化方式:
avg_pool = nn.AvgPool2d(
kernel_size=2,
stride=28
)
max_pool = nn.MaxPool2d(
kernel_size=2,
stride=28
)
adapt_max_pool = nn.AdaptiveMaxPool2d(
output_size=1
)
在过后定义函数的调用
def stack_customized_max_pool(x):
x = conv(x)
out = max_pool(x)
return out
def stack_customized_avg_pool(x):
x = conv(x)
out = avg_pool(x)
return out
def stack_self_adapted(x):
x = conv(x)
out = adapt_max_pool(x)
return out
接着我们定义主函数:
if __name__ == '__main__':
solution_list=[stack_customized_avg_pool,stack_customized_max_pool,stack_self_adapted]
x = torch.rand(128, 1, 28, 28)
for i in solution_list:
start = time.time()
for _ in range(5000):
out = i(x)
end = time.time()
print(f'{i}的时间为:')
print(end-start)
print(out.shape)
最后打印结果为:
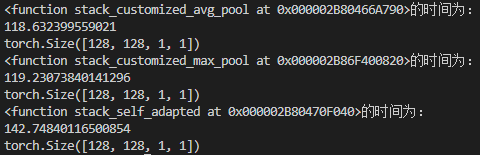
其中,自适应函数的运行原理为:
通过输入的output_size计算得到kernel_size、stride两个参数,padding参数默认为0。
计算公式如下:

3 结语
通过实验经过了许多次的定量循环实验,过程中我们也产生过了其他的方式,但是都没有这样的来得明显,再经过查阅了一定的资料,最终我们发现自适应最大值池化和两种自定义池化的效率为:最大值池化 ≈ 均值池化 > 自适应池化。