最小二乘法

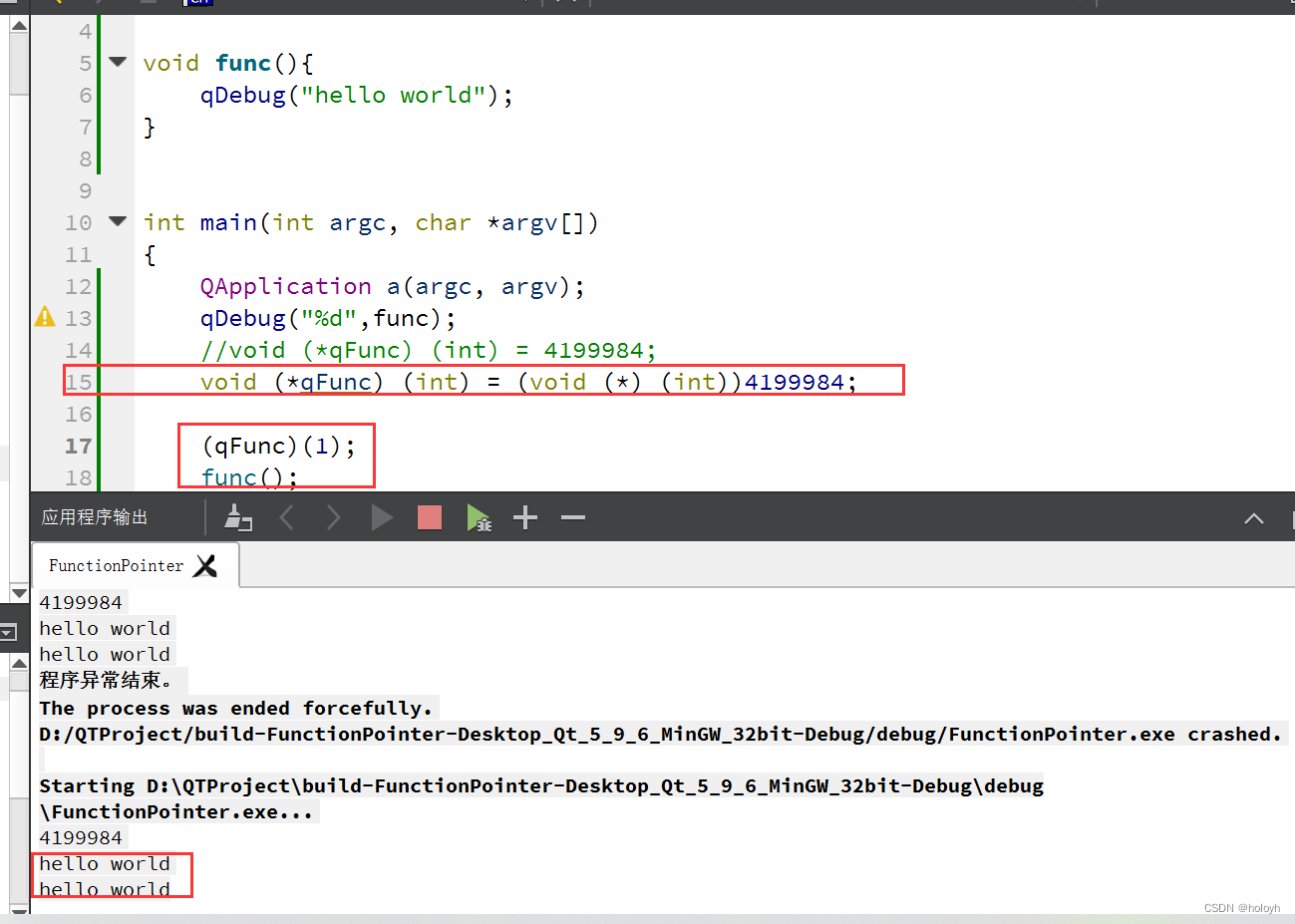
scipy.sparse.linalg实现了两种稀疏矩阵最小二乘法lsqr和lsmr，前者是经典算法，后者来自斯坦福优化实验室，据称可以比lsqr更快收敛。

这两个函数可以求解$Ax=b$，或${\mathrm{argmin}}_x\Vert Ax-b{\Vert }^2$，或${\mathrm{argmin}}_x\Vert Ax-b{\Vert }^2+d^2\Vert x-x_0{\Vert }^2$，其中$A$必须是方阵或三角阵，可以有任意秩。

通过设置容忍度$a_t,b_t$，可以控制算法精度，记$r=b-Ax$为残差向量，如果$Ax=b$是相容的，lsqr在$\Vert r\Vert ⩽a_t\ast \Vert A\Vert \cdot \Vert x\Vert +b_t\Vert b\Vert$时终止；否则将在$\Vert A^{T}r\Vert ⩽a_t\Vert A\Vert \cdot \Vert r\Vert$。
如果两个容忍度都是$10^{-6}$，最终的$\Vert r\Vert$将有6位精度。

lsmr的参数如下

lsmr(A, b, damp=0.0, atol=1e-06, btol=1e-06, conlim=100000000.0, maxiter=None, show=False, x0=None)

参数解释：

• A 可谓稀疏矩阵、数组以及线性算子
• b 为数组
• damp 阻尼系数，默认为0
• atol, btol 截止容忍度，是lsqr迭代的停止条件，即$a_t,b_t$。
• conlim 另一个截止条件，对于最小二乘问题，conlim应该小于$10^8$，如果$Ax=b$是相容的，则conlim最大可以设到$10^{12}$
• iter_limint 迭代次数
• show 如果为True，则打印运算过程
• calc_var 是否估计(A.T@A + damp**2*I)^{-1}的对角线
• x0 阻尼系数相关

lsqr和lsmr相比，没有maxiter参数，但多了iter_lim, calc_va参数。

上述参数中，damp为阻尼系数，当其不为0时，记作$\delta$，待解决的最小二乘问题变为

$$\left[\begin{array}{c}A\\ \delta I\end{array}\right]x=\left[\begin{array}{c}b\\ \delta x_0\end{array}\right]$$

返回值

lsmr的返回值依次为：

• x 即$Ax=b$中的$x$
• istop 程序结束运行的原因
• itn 迭代次数
• normr $\Vert b-Ax\Vert$
• normar $\Vert A^T(b-Ax)\Vert$
• norma $\Vert A\Vert$
• conda A的条件数
• normx $\Vert x\Vert$

lsqr的返回值为

• x 即$Ax=b$中的$x$
• istop 程序结束运行的原因
• itn 迭代次数
• r1norm $\Vert b-Ax\Vert$
• r2norm $\sqrt{\Vert b-Ax{\Vert }^2+{\delta }^2\Vert x-x_0{\Vert }^2}$
• anorm 估计的Frobenius范数$\bar{A}$
• acond $\bar{A}$的条件数
• arnorm $\Vert A^{T}r-{\delta }^2(x-x_0)\Vert$
• xnorm $\Vert x\Vert$
• var $(A^{T}A{)}^{-1}$

二者的返回值较多，而且除了前四个之外，剩下的意义不同，调用时且须注意。

测试

下面对这两种算法进行验证，第一步就得先有一个稀疏矩阵

import numpy as np
from scipy.sparse import csr_array

np.random.seed(42)  # 设置随机数状态
mat = np.random.rand(500,500)
mat[mat<0.9] = 0
csr = csr_array(mat)

然后用这个稀疏矩阵乘以一个$x$，得到$b$

xs = np.arange(500)
b = mat @ xs

接下来对这两个最小二乘函数进行测试

from scipy.sparse.linalg import lsmr, lsqr
import matplotlib.pyplot as plt
mx = lsmr(csr, b)[0]
qx = lsqr(csr, b)[0]
plt.plot(xs, lw=0.5)
plt.plot(mx, lw=0, marker='*', label="lsmr")
plt.plot(qx, lw=0, marker='.', label="lsqr")
plt.legend()
plt.show()

为了对比清晰，对图像进行放大，可以说二者不分胜负

接下来比较二者的效率，$500\times 500$这个尺寸显然已经不合适了，用$2000\times 2000$

from timeit import timeit

np.random.seed(42)  # 设置随机数状态
mat = np.random.rand(500,500)
mat[mat<0.9] = 0
csr = csr_array(mat)
timeit(lambda : lsmr(csr, b), number=10)
timeit(lambda : lsqr(csr, b), number=10)

测试结果如下

>>> timeit(lambda : lsqr(csr, b), number=10)
0.5240591000001587
>>> timeit(lambda : lsmr(csr, b), number=10)
0.6156221000019286

看来lsmr并没有更快，看来斯坦福也不靠谱(滑稽)。