A~D比较简单就不写了，哎嘿

E. Negatives and Positives

给出一个数组a，可以对数组进行若干次操作，每次操作可以将相邻的两个数换为它们的相反数，求进行若干次操作之后能得到数组和的最大值是多少。

思路：最大的肯定是把负数都变成正数吧，从这里开始考虑，对于两个相邻的数为--的，可以进行一次操作让它们变为++；对于类似-+-这样的，可以进行若干次操作使得所有的数都变为正数：-+- -> +-- -> +++。所以对于数组中负数个数为偶数的，所有的负数都可以被变成正数；对于负数个数为奇数的，若要得到最大的值，应当保留绝对值最小的那个数为负值。

AC Code：

#include <bits/stdc++.h>

typedef long long ll;
const int N = 2e5 + 5;
int t, n;
ll a[N];

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    std::cin >> t;
    while(t --) {
        std::cin >> n;
        ll cnt = 0, min = 2e9;
        for(int i = 1; i <= n; i ++) {
            std::cin >> a[i];
            min = std::min(min, abs(a[i]));
            if(a[i] < 0) cnt ++;
        }
        ll sum = 0;
        for(int i = 1; i <= n; i ++) {
            sum += abs(a[i]);
        }
        if(cnt & 1)
            sum -= 2 * min;
        std::cout << sum << '\n';
    }
    return 0;
}

F. Range Update Point Query

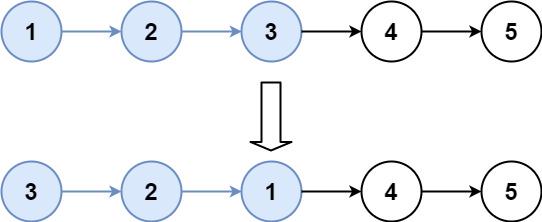
给出一个序列a，有两种操作，一个是对于区间[l, r]内的数进行如下操作：将数替换为所有位的数字之和；一个是给出x，输出位于x的数。

思路：树状数组裸题练习。用树状数组维护前缀和，每次进行操作就在区间内+1，看数据范围，范围内最大的数经过3次操作后也会变成一位，后面就不变了，所以显而易见，我们维护的前缀和的含义是修改次数，输出结果的时候加入判断即可。

AC Code：

#include <bits/stdc++.h>

typedef long long ll;
const int N = 2e5 + 5;
int t, n, q;
int c[N], a[N];

int lowbit(int x) {
    return x & -x;
}

void update(int pos, int x) {
    for(; pos <= n; pos += lowbit(pos)) {
        a[pos] += x;
    }
}

int query(int x) {
    int tot = 0;
    for(; x > 0; x -= lowbit(x)) {
        tot += a[x];
    }
    return tot;
}

int getnum(int x) {
    int num = 0;
    while(x) {
        num += (x % 10);
        x /= 10;
    }
    return num;
}

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    std::cin >> t;
    while(t --) {
        std::cin >> n >> q;
        for(int i = 1; i <= n; i ++) {
            std::cin >> c[i];
        }
        for(int i = 0; i <= n + 1; i ++) {
            a[i] = 0;
        }
        while(q --) {
            int op;
            std::cin >> op;
            if(op == 1) {
                int l, r;
                std::cin >> l >> r;
                update(l, 1);
                update(r + 1, -1);
            }
            else {
                int x;
                std::cin >> x;
                if(c[x] < 10)
                    std::cout << c[x] << '\n';
                else {
                    int cnt = query(x);
                    cnt = std::min(3, cnt);
                    int num = c[x];
                    while(cnt --) {
                        num = getnum(num);
                    }
                    std::cout << num << '\n';
                }
            }
        }
    }
    return 0;
}

G1. Teleporters (Easy Version)

给出一个有0~n个点的数轴，1~n每个点有一个传送门，每走一步会消耗一个金币，走传送门也有相应的消耗a[i]，每个传送门只能走一次，传送门会传送到0点，问最多可以走几个传送门。

思路：每个传送门的消耗是到达步数+传送门消耗，排序，贪心求解即可。

AC Code：

#include <bits/stdc++.h>

typedef long long ll;
const int N = 2e5 + 5;
int t, n, c;
ll a[N];

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    std::cin >> t;
    while(t --) {
        std::cin >> n >> c;
        int cnt = 0;
        std::vector<int> vec;
        for(int i = 1; i <= n; i ++) {
            std::cin >> a[i];
            vec.push_back(i + a[i]);
        }
        std::sort(vec.begin(), vec.end());
        for(int i = 0; i < (int) vec.size(); i ++) {
            if(vec[i] <= c)
                cnt ++, c -= vec[i];
        }
        std::cout << cnt << '\n';
    }
    return 0;
}

G2. Teleporters (Hard Version)

给出一个有0~n个点的数轴，1~n每个点有一个传送门，每走一步会消耗一个金币，走传送门也有相应的消耗a[i]，每个传送门只能走一次，传送门会传送到0点或n+1点，问最多可以走几个传送门。

思路：因为现在位于点0，所以对于从那个点开始，需要我们讨论。然后，对于其他点，我们可以选择从两侧哪一侧到达，可以枚举起点，对于其他点采用前缀和维护消费，二分查找答案，具体细节看代码。

AC Code：

#include <bits/stdc++.h>

typedef long long ll;
const int N = 2e5 + 5;
int t, n, c;
ll b[N];
std::pair<ll, ll> a[N];

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    std::cin >> t;
    while(t --) {
        std::cin >> n >> c;
        ll ans = 0;
        for(int i = 0; i < n; i ++) {
            int m;
            std::cin >> m;
            a[i].first = std::min(m + i + 1, m + n - i);
            a[i].second = m + i + 1;
        }
        std::sort(a, a + n);
        for(int i = 0; i < n; i ++) {
            b[i + 1] = b[i] + a[i].first;
        }
        for(int i = 0; i < n; i ++) {
            if(a[i].second <= c) {
                int l = 0, r = n;
                while(l < r) {
                    int mid = (l + r + 1) >> 1;
                    ll sum = b[mid];
                    if(mid > i)
                        sum -= a[i].first;
                    if(a[i].second + sum <= c)
                        l = mid;
                    else
                        r = mid - 1;
                }
                ans = std::max(ans, (ll)l + 1 - (l > i));
            }
        }
        std::cout << ans << '\n';
    }
    return 0;
}