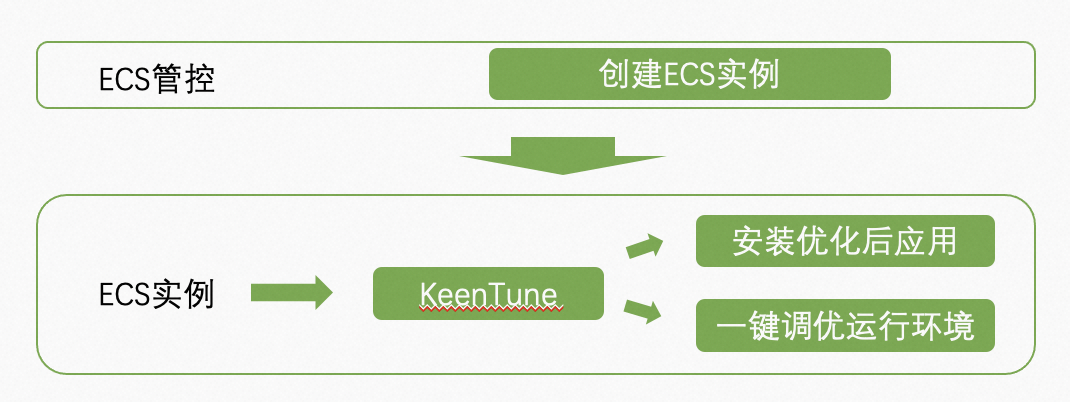
给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径，这条路径上所有节点值相加等于目标和 targetSum 。如果存在，返回 true ；否则，返回 false 。

叶子节点 是指没有子节点的节点。

示例 1：

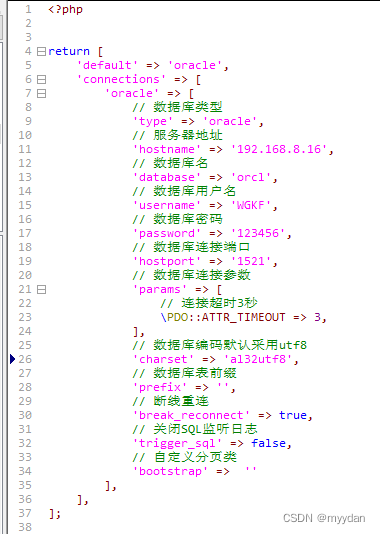
输入：root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22

输出：true

解释：等于目标和的根节点到叶节点路径如上图所示。

示例 2：

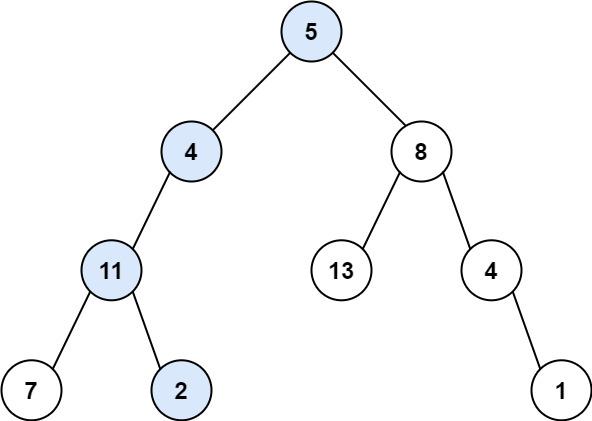
输入：root = [1,2,3], targetSum = 5

输出：false

解释：树中存在两条根节点到叶子节点的路径：

(1 --> 2): 和为 3

(1 --> 3): 和为 4

不存在 sum = 5 的根节点到叶子节点的路径。

示例 3：

输入：root = [], targetSum = 0

输出：false

解释：由于树是空的，所以不存在根节点到叶子节点的路径。

提示：

• 树中节点的数目在范围 [0, 5000] 内

• -1000 <= Node.val <= 1000

• -1000 <= targetSum <= 1000

112. 路径总和 - 力扣（Leetcode）

思路：

对于当前的节点来说，可以判断其左右节点到叶子节点的路径和是否为 targetSum - root->val 。
若是当前节点为叶子节点，判断一下若是 targetSum 等于当前节点的值，返回 true，否则返回 false

c++:

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool hasPathSum(TreeNode* root, int targetSum) {
        if(root == nullptr) {
            return false;
        }

        if(root->left == nullptr && root->right == nullptr) {
            return targetSum == root->val;
        }

        if(root->left != nullptr && root->right == nullptr) {
            return hasPathSum(root->left, targetSum - root->val);
        }

        if(root->left == nullptr && root->right != nullptr) {
            return hasPathSum(root->right, targetSum - root->val);
        }

        return hasPathSum(root->left, targetSum - root->val) || hasPathSum(root->right,targetSum - root->val);  
    }
};