目录
- Zero-complexity (上交复试题)
- 题目:
- 代码:
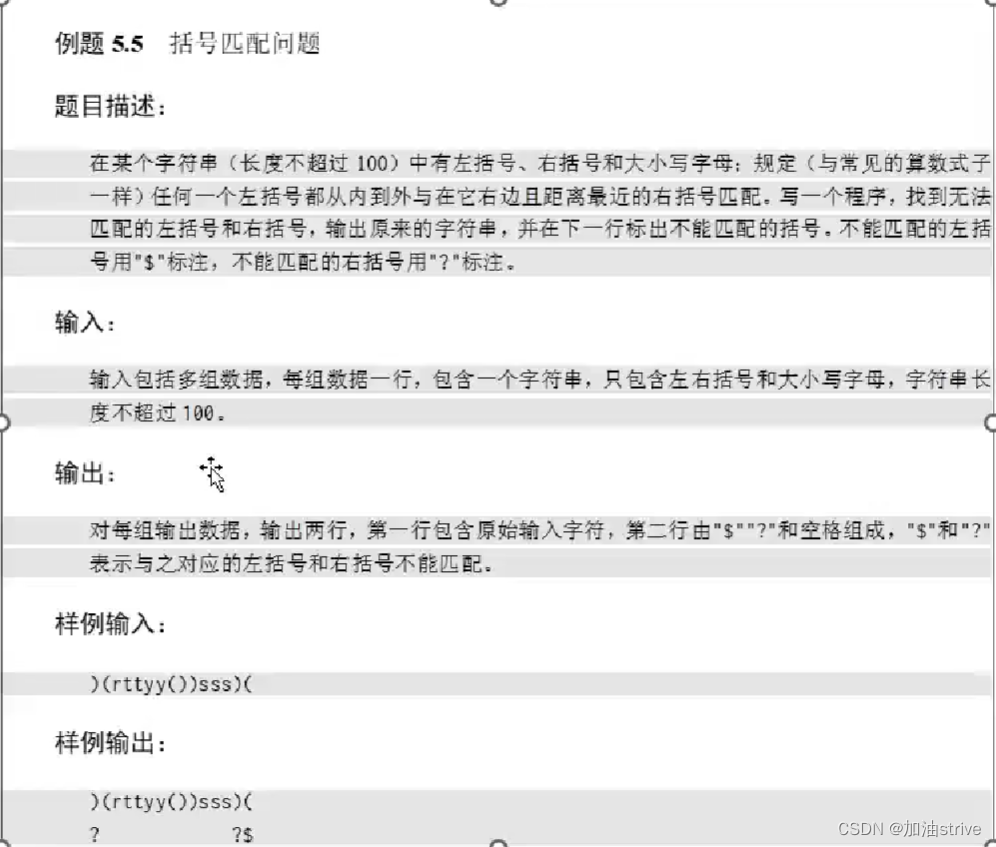
- 括号匹配问题
- 题目:
- 代码:
- 表达式解析问题 (浙大机试题)
- 题目:
- 代码:
标准库里提供了栈
stack<typename> myStack
.size() 栈的大小
.push() 压栈
.top() 获取栈顶元素
.pop() 弹栈
.empty()判断栈是否为空
整数的数据类型

Zero-complexity (上交复试题)
题目:
You are given a sequence of integer numbers. Zero-complexity transposition of the sequence is the reverse of this sequence. Your task is to write a program that prints zero-complexity transposition of the given sequence.
输入描述:
For each case, the first line of the input file contains one integer n-length of the sequence (0 < n ≤ 10 000). The second line contains n integers numbers-a1, a2, …, an (-1 000 000 000 000 000 ≤ ai ≤ 1 000 000 000 000 000).
输出描述:
For each case, on the first line of the output file print the sequence in the reverse order.
示例1
输入
5
-3 4 6 -8 9
输出
9 -8 6 4 -3
代码:
#include <stack>
#include <cstdio>
using namespace std;
int main(){
// 题目中介绍的数据范围大概是10的15次方,int不可以用
stack <long long> myStack;
int n;
long long num;
scanf("%d",&n);
for(int i=0;i<n;i++){
scanf("%lld",&num); //%lld 读取long long类型的六进制数
myStack.push(num);
}
while(!myStack.empty()){
printf("%lld ",myStack.top());
myStack.pop();
}
printf("\n");
}
读取字符串的操作

括号匹配问题
题目:
代码:
#include <stack>
#include <cstdio>
#include <string>
using namespace std;
int main(){
char buf[200];
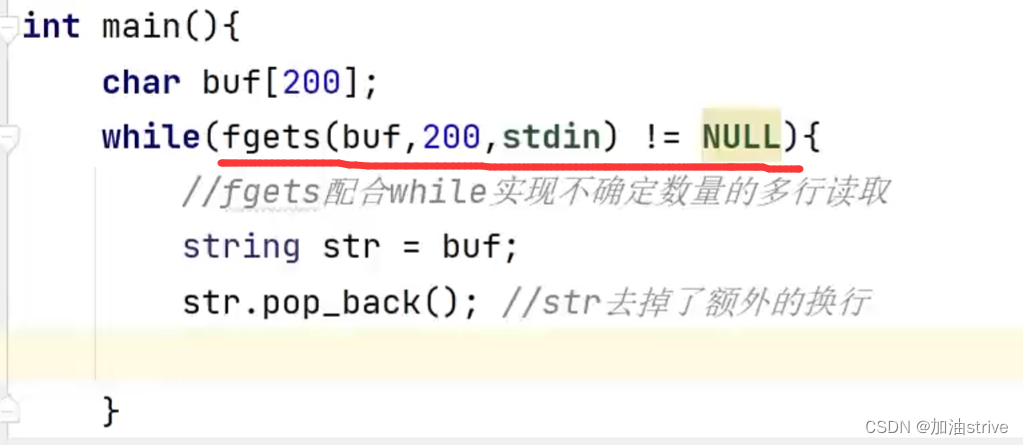
while(fgets(buf,200,stdin)!=NULL){
// fgets配合while实现不确定数量的多行读取
string str = buf; //转化为C++风格的字符串
str.pop_back(); // str去掉了额外的换行
stack<unsigned> indexStack; // 存储了左括号的下标
string res;//保存输出的结果
for(unsigned i=0;i<str.size();i++){
// 如果是左括号
if(str[i] == '('){
indexStack.push(i);
// 姑且认为左括号非法
res.push_back('$');
}
// 如果是右括号
else if(str[i] == ')'){
// 此时栈中没有左括号 非法
if(indexStack.empty()){
res.push_back('?');
}
else{
// 如果合法,栈顶原来左括号下标弹出,res原左括号的值改为空格
res.push_back(' ');
res[indexStack.top()] = ' ';
indexStack.pop();
}
}
// 如果是字母
else{
res.push_back(' ');
}
}
// 输出
printf("%s\n%s\n",str.c_str(),res.c_str());
}
}
表达式解析问题 (浙大机试题)
题目:
读入一个只包含 +, -, *, / 的非负整数计算表达式,计算该表达式的值。
输入描述:
测试输入包含若干测试用例,每个测试用例占一行,每行不超过200个字符,整数和运算符之间用一个空格分隔。没有非法表达式。当一行中只有0时输入结束,相应的结果不要输出。
输出描述:
对每个测试用例输出1行,即该表达式的值,精确到小数点后2位。
示例1
输入:
1 + 2
4 + 2 * 5 - 7 / 11
0
输出:
3.00
13.36
代码:
#include <stack>
#include <cstdio>
#include <string>
#include <map>
using namespace std;
int main(){
char buf[300];
// 设置字符的优先级
map<char,int> priority = {
{'$',0},
{'+',1},
{'-',1},
{'*',2},
{'/',2},
};
while(fgets(buf,300,stdin)!=NULL){
string expr = buf;
expr.pop_back(); //删除末尾的换行符
if(expr == "0") break;
expr.push_back('$'); //补充一个虚拟的终止符
string num;
stack<double> numstack; // 数字栈
stack<char> operstack; // 运算符栈
// 扫描每个表达式中的字符
for(unsigned i=0;i<expr.size();i++){
// 扫描到数字
if(expr[i] >= '0' && expr[i] <= '9'){
num.push_back(expr[i]);
}
// 如果扫描到空格
else if(expr[i] == ' '){
if(num!=""){
numstack.push(stod(num)); // stod --> string to double
num = ""; // num置空
}
}
// 扫描到运算符
else{
if(expr[i] == '$'){
if(num!=""){
numstack.push(stod(num)); // stod --> string to double
num = ""; // num置空
}
}
while(!operstack.empty()&&priority[operstack.top()] >= priority[expr[i]]){
// 新来的运算符的优先级不高于栈顶的优先级
char oper = operstack.top();
operstack.pop();
double rhs = numstack.top();
numstack.pop();
double lhs = numstack.top();
numstack.pop();
switch(oper){
case '+':
numstack.push(lhs+rhs);
break;
case '-':
numstack.push(lhs-rhs);
break;
case '*':
numstack.push(lhs*rhs);
break;
case '/':
numstack.push(lhs/rhs);
break;
}
}
//所有比expr[i]优先级更高的运算符都计算过了
// 接下来吧这个高优先级的运算符入栈
operstack.push(expr[i]);
}
}
// 所有的计算都结束了,此时数字栈中存放的是最终结果
printf("%.2f\n",numstack.top());
}
}