本笔记对应北京大学肖臻老师《区块链技术与应用》公开课第三课。
0.前言
在本节中,肖老师先是简单介绍了哈希指针的概念,然后着重介绍了比特币中的两个重要的数据结构:block chain和merkle tree。
1.哈希指针
谈到比特币中的数据结构,首先就要讲讲哈希指针,对比于传统的指针而言,哈希指针不仅包含指向区块的地址,还额外包含一个哈希值,这个哈希值为地址指向的区块的整体哈希值。
2.区块链
区块链就是由哈希指针连接的,一个一个区块组成的链表
在图2-1中,就是一个简易的区块链,最左边为创世块,最右边为最近更新块,H()就为一个一个哈希指针,其不仅指向前一个区块的地址,同时保存了前一个区块的哈希值。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ICbPpyGH-1677069795443)(https://gitee.com/yu88888//myimage/raw/master/master/image-20211014193644256.png)]
- 此数据结构作用:在上图中,在链中,任何一个区块遭到了修改,在以后的区块中,就可以通过对哈希值的计算,检测到整个系统有数据被纂改。
3.merkle tree
merkle tree是区块链中一个重要的数据结构,存在于每一个区块之中,是用于对交易信息进行保存的数据结构,节点可以通过merkle tree很方便地对交易是否存在进行验证,具体结构如下图3-1所示。
在上图中,最下面一行的tx,称为数据块,代表比特币网络中的交易,此区块中存有8个交易,数据块上面的H()是对底下的数据块整体取哈希,往上的每一块都是对下面的整体取哈希H(),其中最上面两个哈希值取哈希会得到一个根哈希值,根哈希值用处很大。
3.1 区块链中的区块
因为merkle tree通常存在于区块链的区块中,因此不可避免的要对区块链的区块组成进行介绍,为以下介绍merkle tree的作用打下基础。
区块链中的区块是分为块头和块身两部分:
- 块头 Block Header
- 块身 Block Body
块头中包括一下内容(但不限于):
- 根哈希值:merkle tree root hash
- 版本号
- 前一区块的哈希值(我们可理解为哈希指针)
- 时间戳
- 随机数Nonce(后面会讲到)
而块身中包含了该区块的所有信息(比特币是所有的交易,以太币还包括了所有账户信息)
3.2 实现数据防纂改
- 只要记住根哈希值,就可以知道整个tree是否有数据更改。 如果有数据被纂改,那么根据tree的结构,依次往上推哈希值,最后可以得到一个计算后的根哈希值,将此值与之前保存的哈希值进行对比,就可以知道是否有数据更改。
3.3 实现merkle proof
在区块链中有轻节点和重节点之分。重节点保存了区块所有信息,轻节点通常只保存了block header。现在假设某轻节点想知道某笔交易是否写入了某区块中,应当怎么做?
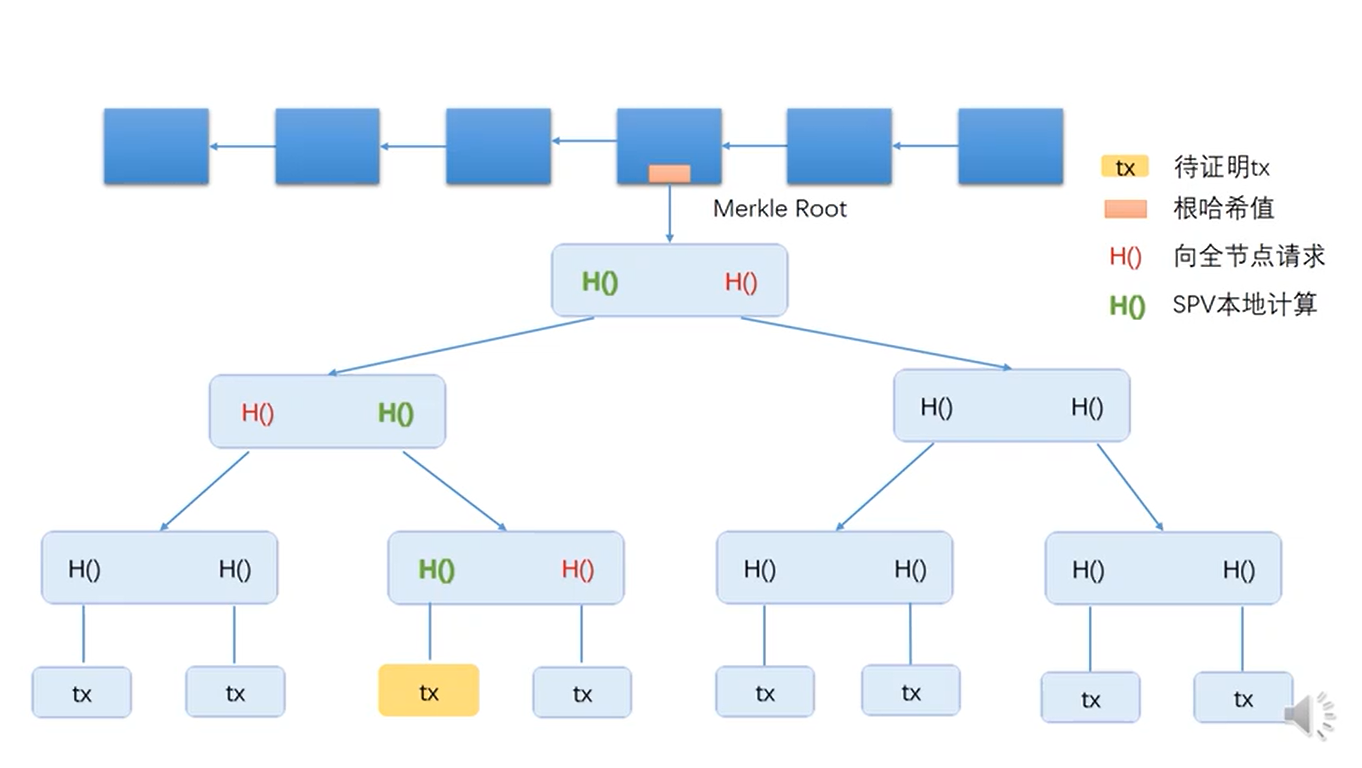
在比特币系统中,使用merkle tree解决这个问题,如下图3-2为解决过程。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-6Av4VJtS-1677069795444)(https://gitee.com/yu88888//myimage/raw/master/master/image-20211014193705672.png)]
假设上图中,轻节点A想知道黄色的tx是否真的存在于第四个区块中,那么A可以向一个重节点进行请求验证。
具体验证过程如下:
- 重节点收到了验证请求,因为重节点保存了整个merkle tree的信息,所以,此节点给A提供3个路径上的必须路径数据(图中红色的H())。
- B在本地对tx进行哈希运算,可以得到倒数第二层的第3个绿色的H(),然后再和之前获得的红色H()一起,在本地算出上方的绿色H(),再和获得的红色H()一起,在本地算出上方的绿色H()……一直循环下去,最终算到root hash值,设为H1。
- 将此H1与轻节点本身保存的根哈希值进行对比,如果相同,则可以证明交易存在该区块内。
在merkle proof中有几个点需要注意:
- 为什么重节点不直接给轻节点发送是否存在某个交易呢?
如果直接发送结果,确实可以节省一点的计算资源,但是我们不能保证所有的节点都绝对安全可靠,我们必须假设有些节点是恶意的,因此我们需要依靠merkle tree,让轻节点自己进行一次验证才可以保证交易安全可靠。(为什么会安全可靠,可以联系前一章中哈希函数的防碰撞性质和单向性仔细评品味)
- 时间复杂度多少?
证明交易存在的时间复杂度为O(log(n))。证明交易不存在有两种算法:1.遍历整个树,时间复杂度为O(n);2.对所有叶节点进行取哈希,然后根据哈希值排序,对待查找的交易取哈希值,进行2分查找,时间复杂度为O(log(n))。
比特币系统中,由于只需要做证明交易存在的任务,所以并没有对树进行排序。